Анмех лекции 2025 Барабанов / АМ_7_Принцип_наименьшего_действия_Л_07
.pdf
]17 Принцип наименьшегодействия Симметрия. Законы сохранения
получили ранее для частиц:
L (rim, I, ii....TEE,"i"
2
Т
ур-ние Лагранжа:
Evil/E-ED
все
пары
* да-7m' "#mili =-Tim, Vij(IT-51) |
|
Σ |
±# Ё |
|
|
докажем независимость относительно выбора СК:
для частицы 73 степени свободы 3Nдля частиц
тогда переход координат: |
|
||
|
(т...., ) (91,92,-„957%, 59,%,-95) |
||
|
обобщённые |
\обобщённая |
|
|
скорость |
||
|
|
координаты |
|
ф-ня Лагранжа: |
|
* |
|
119,g, 17T-V: |
#7g-⅔", 5-5, «3N |
||
докажем, что это |
верно описывает динамику |
||
П |
|
действия(принцип Гамильтона): |
|
(экстремального) |
|
||
|
|
||
Itgets → 119,q.tk T-V, каждой траекториида, |
|||
сопоставим число (действие): sfs.gg#dt, где |
|||
при t",1- начальное и |
конечноевремя, |
|
|
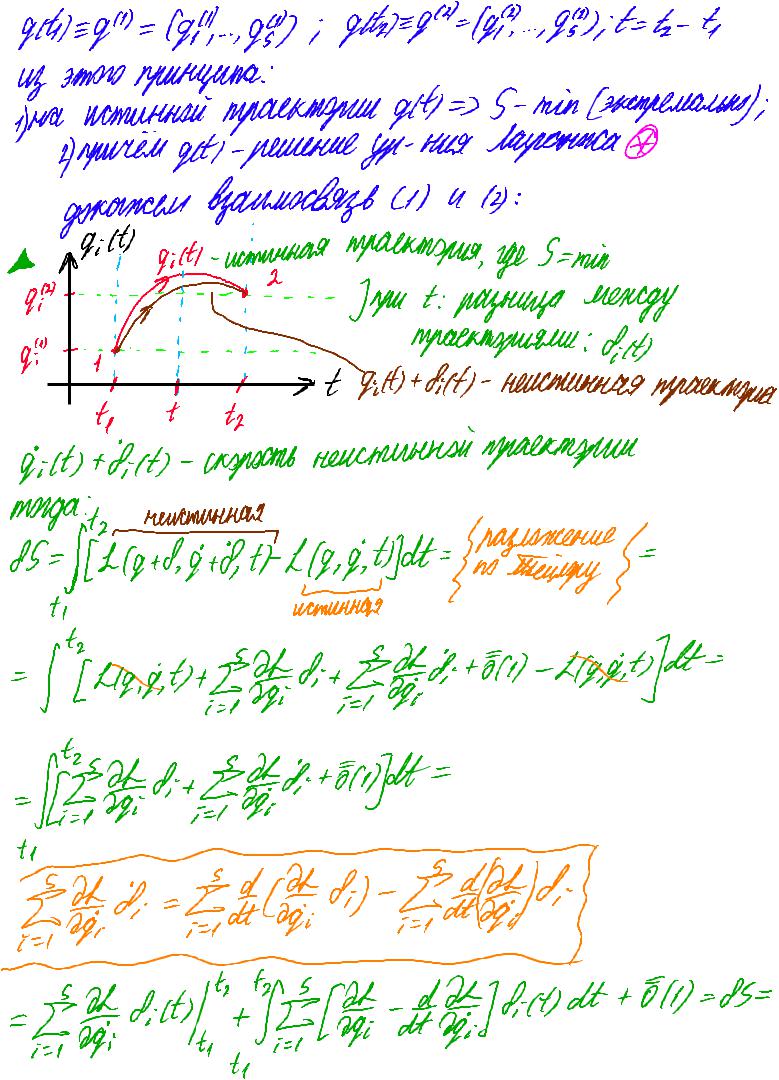
get)-9" = (g,",-„99; 9h79"191....957th-4 |
||||
из этого принципа: |
|
|||
„на |
|
й траектории get, 5- min (экстремально); |
||
г)причёмда,_решениеун-ния Лагранжа |
||||
докажем взаимосвязь а) 44: |
||||
|
gilt) |
gilt,-истинная |
траектория, где 5-min |
|
4" |
|
|
2 |
Зприt: разница между |
9! |
1 |
|
|
траекториями: diet) |
|
t |
gilt)+diet)-неистинная траектория |
||
|
|
|||
|
|
|
||
|
te |
- |
th |
|
Gilt) +diet)-скорость неистинной траектории |
||||
тогда, |
неистинная |
разложение |
||
|
|
|
|
|
85=111(qed.gid.tt-11g,д.that- по Таймру} |
||||
Н½ |
|
истинная |
||
÷ |
[219,91+{ftp.Effzdtm-L#tfdt- |
|||
i-1
½
[иEgg dit:ЕЁ:doubt=
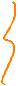EIF.IFE.IE?iEftlld
=[Edicts/"HERE.-А-Ё.JAMMEH-85
5=1 |
+1 t, 51 |
причём dicti-d.lt0=0, i-T
"Elka-Д-Ё.)анаби
t, |
А |
противоречие |
|
1 |
ЗА», если Picts; тогда при -он Асо?
тогда А-0: 9g#Дд-это честь н-ние 
ETS 
* 
Лагранжа
определения:
0д1д =p:-импульс в соотв-щей координате
если 1 не зависит отд, то д:-циклическая
Pi = coast координата
E-ftp.gi-L „диод из ул-ния Лагранжа
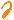
s:P: dtlq.it/=Ey Ё-it.li#iitttΣi-1 27Ё)17
А
get)-истинная
траектория 4-=-#
т.е., если ¥0 East
и
однородность времени
It,д) (7,97: ttft.gs,97-gilt,д) |
|||||
|
|
|
|
#Fett,97, g:-gilt?97 |
|
|
|
|
|
19,д.1) 1195g!ty |
|
12 |
|
|
|
|
|
s-tfllq.it)At-½flat,gift)Attest-min |
|||||
ti |
|
|
te |
ул-ниеЛагранжа |
|
ур-ние Лагранжа |
|
etta» |
|
||
|
|
(t,g) |
|
|
|
если |
(t.gl#Ittgt)-makse, что |
Legit) и LYqigt.tt/оди |
|||
наково зависят от своих аргументов, торечь идёт о преобра |
|||||
зовании |
симметрии |
|
|
||
Пример |
свободное движение частицы вплоскости |
||||
|
у |
9k' |
(поворот СК на угол α) |
||
у' |
x'-хинутd |
||||
|
|
4 |
|
у'-xтLtymd |
|
|
|
|
Х |
|
|
|
|
|
|
1- mktg"= mpity?)=L |
|
|
|
|
|
L Преобразование симметрии |
|
Пример |
|
переход к полярной СК |
|
||
2- Mitt"); 11 minё) -не преобразование |
|||||
|
|
2 |
|
2 |
симметрии |
если |
ta-fit,g,a), 9,1-gilt,g,a), где |
а- непрерывный параметр, |
|||
то преобразование непрерывно |
|
||||
Пример поворот Ск наугол α: параметр a=L
(Нётера)
каждому непрерывному преобразванию симметрии сют-
ветствует свой интеграл движения |
≥ |
|
tr |
ti |
|
5-flegg,tdt-замена =/11999,79A"-
t, 
tea пер-ных 4
'hсдwaвиdнaемFILI991guid.ataida)utada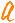 
tilda -12
ti" лит-ние |
fida |
|
| |
|
t |
на µ линт-не ti |
|
|
|
tied |
|
1- Shai", gadatadaydtada-fheqa-
idggaeda.tadaydtad.ie
titi" titi
+fhlqadggada.to/dta--f1(g9ga,ta)fdat
ti ti"-titan |
ti |
tilda |
|
+ 1119,"99,79#"datfhcqadggada.to/dta
72" 
4 
й
1-1-0-17"daL!/111999qaeda, 7)-11999919ft"
71Eliot.EE?7n49
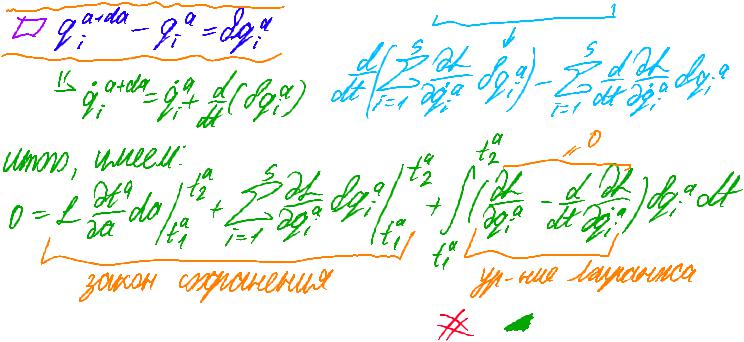
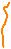qaida-да-877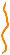
Ё.Gadgil-E.tt# i" |
||
g,999,9#18991 # |
- |
О |
Итого, имеем: „ |
Д |
|
0-1Gtdo/!+Ё.F.li/ttlGatti)did
закон сохранения |
ур-ние Лагранжа |
|
= |