Лекции Михайлов / ТФКП_11_Продолжение_принципов_и_операционное_исчисление_Л_11
.pdf
111 |
Принципы конформного отображения. |
|
|
||||
|
|
|
Продолжение |
|
|
|
|
2)(принцип соответствия границ) |
|
|
|
||||
ааналитическая в области ди непрерывная в Iфия |
|||||||
взаимно.однозначно отображает границ дуг на границу |
|||||||
FДД с сохранением направления обхода, тогда область |
|||||||
д отображается взаимно.однозначно на |
внутренность |
||||||
области ДСБ |
|
|
|
|
|||
|
A4 |
|
г] отображение |
к |
≈ |
w |
|
|
|
|
W-712) |
|
|||
|
|
|
|
|
|||
|
|
|
|
|
|
||
|
G |
|
|
|
|
|
|
|
|
Х |
|
Д. We |
• V2 |
||
|
|
|
|
|
|
Ч |
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
рассмотрим |
Fk)-127-4, не,- точка Д |
|
|
||||
|
v |
5212)= 7121-Wr, 4- внешняя КД точка |
|||||
|
|
w |
|
|
|
|
|
|
|
|
|
|
|
|
|
r А) |
W |
|
|
|
|
|
|
|
|
5,12) |
И |
|
|
|
|
|
|
Щ |
|
|
|
|
|
„совершим полный оборот по гна |
|
|
|
|
|||
при этом толка И совершила полный оборот по Ти |
|||||||
|
|
|
|
28 |
|
|
|
аргумент 412) получил приращениеNarangf,(2) -й |
|||||||
в соотв-вин с принципом аргумента, число нулей |
|||||||
ф.и Ты в области & равно N¼ Varangians |
|
||||||
1,1107=0
Ася-1110)-И,-0 этодля значения
2) |
" |
|
и w |
|
F |
А |
we |
|
|
|
" |
аналогичнодля Пса:
число оборотовпри обходе точкой 7 контура и соотв-но не контура
Гравно о 
Ко-число нулей
Attarargf.ca
т.е. таких точек чеG, вк-ыхА)=И
доказано взаимно-однозначность отображения
Д
3)Принцип симметрии) #
• з в области Gm-сти задана аналитическаяфняна отображающая конформно эту область на область Д пл-сти@ с отображением прямолинейногоучастка.
отрезка reeds на прямолинейныйучасток ТЕД;
тогда область для-ти ч, являющейся ским-ной области дот-но прямой, проходящей через отрезки
можно построить,! образм, |
янв даны |
|
1121, к-ая осуществляет конформное отображение |
||
.→д |
Д.гдеДимметричнаобластиДвпоотп-т |
|
прямой, проходящей через отрезок т |
|
|
возьмём произвольную точку ½ в области д,далее |
|||||||
|
|
r |
|
И |
|
|
|
у |
|
а. симмоеттнриючны" WALL) |
К %" |
3 |
ОТН-НОГ' |
||
|
½. |
1£ G |
|
|
|||
|
|
|
F |
|
|||
Ы |
|
|
→0W Г |
|
|||
|
|
|
|
|
|||
|
|
|
|
V12) |
|
|
|
|
02 |
х |
|
|
|
||
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
возьмём в области G точку 1, сим-ную отн-но прям- |
|||||||
линейного участка |
т подставляем это вфлюиды, |
||||||
получаем W, вплоти берём й, симметричную иоты. |
|||||||
но Г' |
образом построим й(2)-Ай),к-ая осущес. |
||||||
.таким |
|||||||
твляет отображение ЦДД |
|
|
|
||||
по т. о единственности аналитическойф-ни |
|||||||
! |
|
ля ф-ня, совпадающаяна д с |
|||||
112), а на д с фней др) |
|
|
|
|
|||
• аналитичность |
такой ф-ни следует из характера её |
||||||
построения |
|
|
# |
|
|||
(действ-но, W! him °" |
|
|
|||||
|
|
029002 Те |
|
|
|
||
Римана) чая в области д ф-ня с границей, состо
Э |
|
|
ящем более,чем из одной точки, отображающая эту |
||
дна |
сть круга 1421 |
|
Ад |
||
|
||
.для единственности такого отображения требу.
ется дополнительныеусловия: fc2.tw. и argue'на...
Примеры отображения
1) W-акв (подробно разобрано ранее)
2)дробно.линейная ф-ня
W-a9n2+6d ' (♀ ≠ ¼) (with
3m½: у |
Z-geir |
xntt-fe.iq
1
|
инверсия оты-но 121-1 и зеркальное отражение оти. но действительной оси
1222
инверсия без |
сального отражения осуществляет |
ф-ЛЯ W-½
•рассмотрим не#Est-1ˢᵗ
121312
Точки Z =-В
для расширенной [ дейДДТ } конформное
свойства дробно-линейного отображения 1)окружность окружность или прямая
2)точки, аким-ные оти-но окружности отображаются в тачки, симм-ные отн-но её образа
Примеар |
отобразить внутренность 14--1 на верхнюю |
||||
полупл-сть |
|
|
|||
|
у |
|
|
у |
|
|
|
|
x |
|
x |
|
|
|
|
|
|
1 |
|
|
|
|
|
1
по трём точкам границы
170 |
µ-12th |
i |
2+8 |
11- |
|
110: не-ЛЁД
11s:
AREA
171: 1=41 Я-ft"
Ей
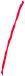wish
л y |
Ц |
Ж |
Н |
Ш-Z-21
1- 4
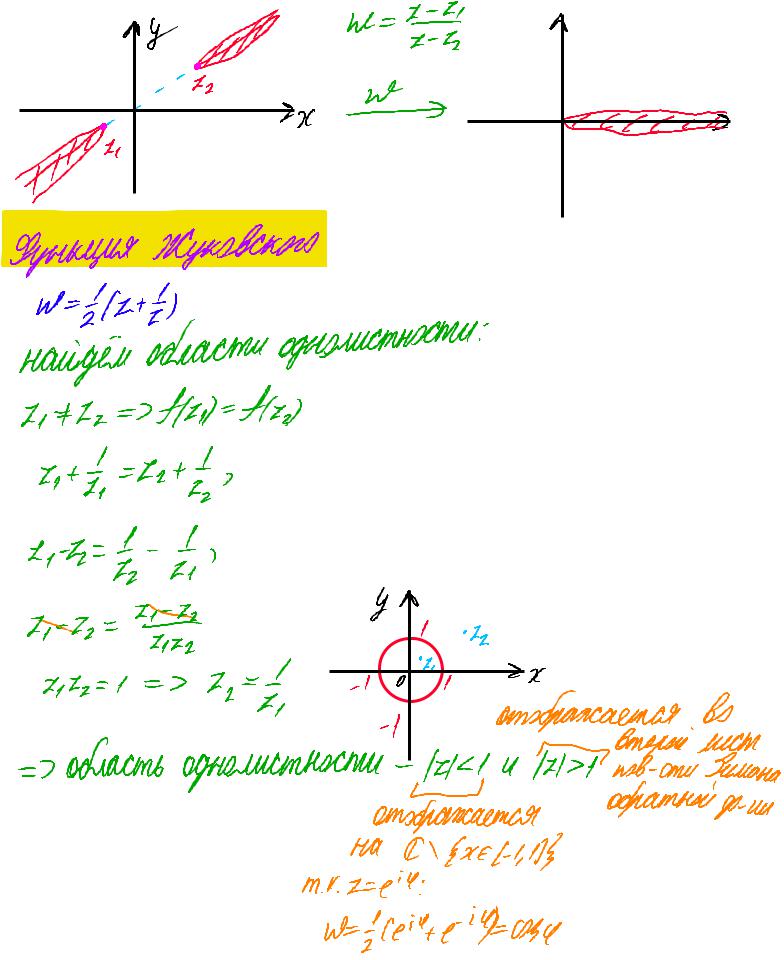
Функция Жуковского
W-1121½)
найдём области однолистности: 71722 An-А(4)
4,+ ½, -11½
11-titi ½,' |
y |
|
|
|
21-22 = 21-22 |
|
|
|
|
|
|
22 |
|
|
1172 |
|
|
x |
|
7112=1 22=1 |
|
¼ |
|
|
1 |
О |
|
|
|
|
отображается во |
|||
|
1 |
|||
|
|
второйлист |
||
|
|
|
|
|
область однолистности-1421 и 12171 кости Римана |
||||
|
отображается |
обратнойфии |
||
|
на |
¢ \ {ХЕ/-1,11} |
|
|
|
m.K.IE'4: |
|
|
|
|
ntfceil.ee-"9034 |
|
||
Приложения к операционному исчислению. Интегральное преобразованиеЛапласса
офим fit, ставится всоотв-buefepi-fe.pt#dt-ин-
теграл Лапласса, tek, pea ◦
fit)-оригинал, Еф-изображение оригинала т
Лаплассу.fi, удовлетворяет условиям:
1)задана при +20, при to А-0
ft)=fit)еbдolин)t ичная ф-ля Хевисайда
o.to 8th 1, to
2)НА конечном
промежутке А)имеет неболее конечногочисла точек разрыва 1мда, причём
Аточекразрыва 2рода
3)A),при t → +0, имеет ограниченную степеньроста, me-Atik eatМ, ах, а-показатель степени роста
далее доказывается, что Fcp аналитична вполу- н-сти Лера
свойства
1)если fit):f(p), то|.ΣLift)#EILFIN
2)если felt):IF(2)
3) (теорема запаздывания) |
|
|
fits-{ater ёпт) |
|
t |
ft)-1,177 |
Ч |
4)A'"chip"1)-79-Дд-...-A""10
р"
5) интеграл от свёртки
t
Shut-adr-FMF.CM
О
свёртка
6)Inde:IFM
7)Рф,÷ 1-1774
8)fpdpiAM¼.
р 
9) (теорема смещения)
F(М):ЕР"AH
обратное преобразование |
|
|
Paix |
|
преобразование Меллина: |
У |
|
||
|
|
|||
|'-t Flp) ftp.tifiertflpdp |
|
|
|
Х |
|
|
|
Х |
|
|
|
|
|
|
|
|
|
↓ их |
|
|
|
|
|
|