Лекции Михайлов / ТФКП_6_Свойства_сумм_Ряды_Тейлора_и_Лорана_Л_06
.pdf
при точечной сх-сти в определении на месте добавляется условие «Д
. 514Th, Ик(2)
• критерий каши равномерый сх-сти ряда А) внекой
области Д:
(*)-И-СЯ К 512) в области Дравномерно
V60 INE: MM, PEN /Snip(2)-SNAKE, VIED
1 
а) -х-ся к 512) в Дравномеры
оценим/Snap 14-5m12)/=/Snap(2) -512) +5121-5,12)/≤
≤ (Snap 12)-514/+154121-512)/«
т.к. А) х-Ся к 5171 в Д равномерно
V60 INE: MM, PEN /Snip(2)-SNAKE, VIED
2) V60 INE: NNE, PEN 15pA)-51214, HED
рассмотрим произвольную АД, получаем числовойряд
Ён-для него доказан критерий кожи, т.е. вданной точке Ем сходится к числу 512)
на области
Д определена 512)-сумма Ёn
обобщим АД:/Sup 6) -5h17))£15117-5nA)/4
фиксируем и, рях, получаем ) . 
опр-ниеравномерном схсти (*)
Т ДУ, признак Вейерштрасса, мажорантный признак 
равномерной сксти функционального рядаа) вобластиД
• абсолютно сходящийся числовойрядЕа,-мажорирующий#
4=1
ОДЕН."KE.la/kED/ а) сходится равномерно в Д
• введём обозначение 5121-5nA)-12)-остаточный
1-£412) член
Kent
пристсти А) In(2)КЕ
рассмотрим Innit1512)-Sn(ДЕТИ»/≤Ёмкн |
|
|
КЕНЫ |
LEEK LE |
|
ввиду ИстиЁ. a" |
|
In»НЕ # |
|
свойства суммравномерно сходящихсярядов
Теоремы Вейерштрасса
ТО.равномерно сходящийся ряд из непрерывных вобласти Д функций сходится в Д непрерывнойф-ней
аналогичнаяформулировка: (дни-равномерно нася, имеет,#нет )
s
ДИНАД)
переобозначим 514=У,4175 используем одно из определений непрерывнойф-ни:
{>0 740:1078 10514
1051=1512102)-51271=512+02)-Snip (2+02)+5up(1+02)-
13
-5m12)+5^17)-512)/≤ 1512+02)-51%2+07714Snep12102)-51st + ,5m41/« т.к. рядравномерно сая m.x.sn, same,
#
т.к.ряд равномерно 
скся
.равномерно сходящийся вобласти Д из непрерыв ных ф-ий можно посленно интегрировать вдольнекой
кусочно-падкой ССД * аналогичная формулировка:
Тинг)-равномерно схся вД,ЭССД- кусочно-гладкая, *I WEN UNDEAD) „Σ" Сfun(7)dL =/£, unfolds
11-ая теорема Вейерштрасса о пленномдядь-ним)
• если ряд из аналитических до-ий ипса вДсхся
взамкнутой подобласти равномерно, то аможно
вподобласти почленно дифференцировать кол-вораз
аналогичная формулировка:
]£412)равномерно скся вкподобласти Д .
*' ила 8D,нет»
Ё. ты-равномерно схая во б/д
(2-ая теорема Вейерштрасса)
• если ряд из аналитических в области Д а-аравно- 
на дД сх-сяравномернона всей Дбд
-докажем →{side[,lunch-? 15127£1411 
me.({sends-Ё. fundЕ-оценим
с
I{sends-≤,"Incan≤/{radar4ᵗʰ.ge1кривой-длинас
#
Степеннойряд
. Теорема Тейлора
Степеннойряд: Σс„12-207,"1.-фиксированная
11=1 €[
. часто ИСПОЛЬЗУЮТ £42"
• рассмотрим область""абсолютнойсходимости вточкег, получаем числовойряд; подоле Коми(Даламбера)
кlt-2.1"21 если 14-ряд ская
131-рядраская
ТА 12-2014, 12-2014mвn =R
ms 1cal
возьмём подобласть кругах-сти (рассмотримзамкнутую подобласть 12-442
тогда имеется мажорирующийряд
Ёж-21Ёки" £112-нам |
|
WI 4=1 |
равномерно |
|
к аналитическойф-ни |
(теорема Абеля)
если спеленной ряд и-я в 71710, то он х-я z:
12-101421-101, внутрикруга 12-24/11-74сх-аяравная-
но к аналитической ф-ни
рассмотримΣ с„(2-201":Ей и,-20)"-a-a
4=1
{аск-го)"}-х-ая, т.е. она ограничена(С. 14-207"/и
lcnkyМ-z.tn, |
|
me.ряд":-[411107401997 |
Ё.144-701%52-24" |
|
|
4=1 |
121-101" |
ется рядом геом-койпрогрессии, |
|
||
mangaЁлки"-сксяравномерно каналитической
ф-им
„ 
. если [612-10)"раст-ся в22, то онрасхая 2:
NII
11-2017 122-71 (следует из предположения от противного
• из прошлого следствия им.Абеля:Эко:
[Calero)" схся при 12-42 ирасх-ся 12-7012
же (по окр-ти 17-201-Арассматривают отдельно)
(нахождениерадиуса стали)
• имеет место формула кожи-Адамара:
Rte'l-lim Tal ns
или формула Даламбера: Ref, 1=1141
(Тейлора) сая |
внек-ом круге 12-1012ф-ня7) |
|
|
в виде степенногоряда: |
|
АН-Ежи-н"-определён однозначно |
||
y |
R |
-2 в круге, |
• |
0 |
построим окр-стьрадиусам, |
28 Ф |
включающую 2 |
|
|
|
х вкруге12-101ср применима |
интегральнаяфла коли:
1-¥114 11-10µ
96-1 - 59
|
1 . |
|
л 2-70 n |
41=9-1-10170 |
= (в-10) (1-2-10) |
|
1-10 тов-ю |
|
1-7 |
|
|
|
разложение#-Est", ни |
||
тогда: |
« |
Cn (1-10)" |
|
|
|||
E-tile.tl?E.ETE |
|
||
а |
я |
|
|
cnet.c,lt19-2)"и
щфлы Кони In-17420)
me. 1=717012-70)"
no n!
Ряд Лорана
Ряд Ирана: Ёc.cz-г.)"-Ё612-207"+£72-10)"
11=-8 FO | 4--х
Сх-ся внутри круга скати
12-2014
•рассмотрим *:
Ein-ы"-см-7.Мак-2054...Ё и
N 12-10)"
обозначим,1. =} Ес.„§"-степеннойряд, к-ый
1=1
а-а:/{Кв или ½. 121 или 12-41-1
внешность нек-от круга
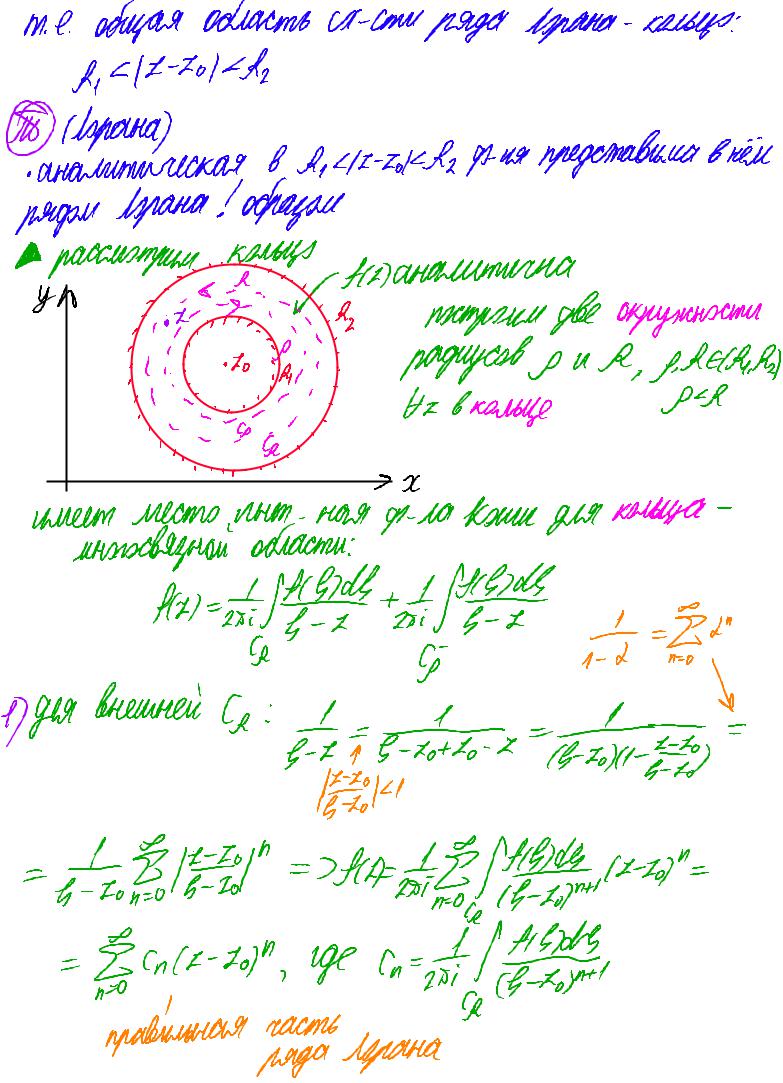
т.е. общая область сх-стирада Ирана-кольцо: |
||||
A, 41-70142 |
|
|
||
(Ирана) |
в Я,42-42, ф-ня представила внём |
|||
• аналитическая |
||||
Ирана!образом |
|
|
||
рассею |
кольцо Нааналитична |
|
||
y |
|
|
построимдве окружности |
|
|
• L |
|
||
|
• 70 |
А |
радиусовPUR,PIERA |
|
|
|
|
ля |
|
|
|
|
а вкольце |
|
имеет место пыт-ная ф-Сла Коми для кольца- |
||||
многосвязной |
области: |
|
|
|
|
fat felids+д.feli1ds |
, |
||
|
2й 1- 2 |
§ |
1-2722" |
|
|
а |
|||
|
|
|
|
1 |
1)для внешней Cri fists.-21-7014-Ёй- |
||||
|
|
47.4 |
|
|
=417176 |
" A##Ё.1114174"= |
|||
= Ent-701", где |
Alds |
|||
cut/д (9-20)"+1 |
||||
|
| |
часть |
|
|
правильная |
|
|
||
|
|
ряда Ирана |
|
|
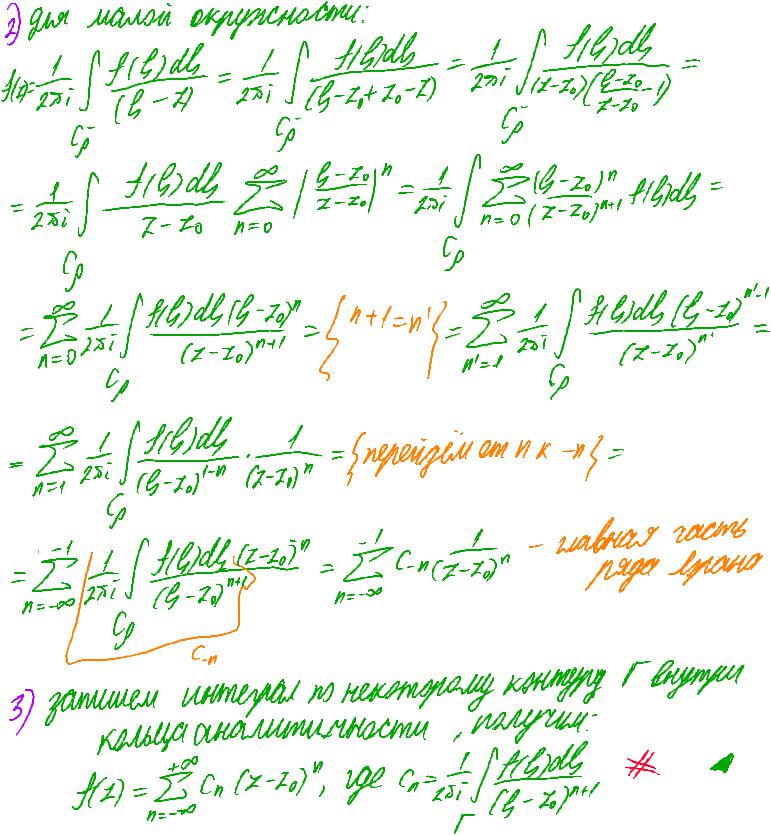
для малой окружности:
|
|
|
|
|
М |
artist!¼-÷/д."!!stillвness |
|||||
5 |
5 |
|
|
5 |
|
=#ftends-/в-7. |
"§ 2-7 14-201" |
||||
|
Σ 1- 70 |
-2-й 4=0 (Z-2)41 1)@ = |
|||
2- 10 11=0 |
|
|
|
|
|
д |
|
|
д |
|
|
|
|
|
|
|
|
=.EE!1941520" |
|
|
felids (в-18"" |
||
|
(Z-107441 = |
"""'/:&:! |
(2-20)"" |
||
с |
|
|
|||
|
|
|
|
|
|
|
12-7in |
=/перейдём от пк-из= |
|||
-Ё.£94. 1 |
|
|
|
|
|
(в-2) 1-„ |
|
|
|
|
|
, |
|
|
|
|
|
TEH143m12-207"=4=-8 |
C-н (2-20)" -moldряда Ирана°o° |
||||
д |
C-и |
|
|
|
|
|
|
|
|
|
|
3) запишем |
интеграл по некоторому контуру внутри |
||||
кольца аналитичности, получим: |
|
||||
А1) =, |
Cn 12-20)", |
где cast |
Н dls |
|
|
|
|
|
р |
1- 2)41 |
|