Лекции Михайлов / ТФКП_8_Вычеты_Л_8
.pdf
Л8 3) существенно особая точка П ((охотского-Вейерштрасса)
• влюбой окрестности существенно особой точки находит. я такая точка 2, вкоторойдля любого комплексного числа
ВИКЕ» 18171-BILE
от противного: Аокрестность существенно особой точки 7=20,в которой при некотором комплексном числе В. к 4.a
17171-Вор Е. , тогда µ-„≤½. д1» ограничена
вокр-сти по т. обустранимой особой точке:
*-да = (2-707412), |
412070, M 70 111)-Bo/=#17705,"me. |
20-ПОЛЮС ф-ни 7121-В и ф-ни 7127-#12-105"+ В - |
|
- противоречие |
(при то устранимаяточка) |
(т.К. 10-существенно 
особая точка)
Вычеты
. это относится к изолированным особым точкам
• 12=20-изолированная особаяточка однозначной анали тической ф-ли, тогда она разложила! образом в и
вряд Лорана (вкольце аналитичности вокруг 2--7,
712)-Elen 12-207", где on-stiff94
(в- 20)"-4
ватыitвает только
одну особую точку 2=70
вчастности, a-a: C-1-fifth)d
данный интирал с-1-#filth-вычет 9-ш
111) в 2=20
обозначение: ВыAn,7.Fresh),29
Дополнительныеформулы для вычисления вычета 1)вычет вполежен-го порядка ф-ни * тогда ряд Лорана:
1) £2", +асужджит..-£1 + Со + 412-70) +412-7014... • (7-20)"
(2-10)%2) - С_ „+ [„, (2-70) +... + C,(2-70)"76(2-70)"+6(2-20)"#...
продифференцируем обе части Сп-1)раз
ditkr.int-к-нсна».1617-20+(4+1)п...)612-107.
устремил 7 → 70
hm a" |
|
1-to den-1 (12-20)"А1-(n-Да, |
|
получаем для a: |
„ |
C-i-resl1.27-ahlsl.n.6-2.my плюс 
п-го порядка
Пример 1127=112117" 251-полюс и-го порядка
rested,-A(П-'1)!2lo→in, dden"-1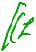 
+1)"¥1711311:(2) =
(22")"= 2m22""; (22")"= 212m-1) 22m²;.
(22")"-"= 2h12m-1)... (24-(n-21/22"-"-"-212N-1)..-112) 2""
1127"-"½, = 2h12m-1)..-9+21611""
resAn-Fatman-1-1+2161""
2)полюс 1- и порядка
рассмотрим 4) случай прие п-1:
res(17), 70]-114. 11-717) |
-для, например, ф-ни |
|
вида 11)= 41" |
||
|
||
|
1-10 |
3)полюс 1- и порядка если же в полюсе 1-го порядка,ф-ня имеет вид:
711=417 |
, 41270, И) имеет ноль 1- го порядка: |
(2) |
V12)-Hid (2-70)+47142-1077... |
4
½#41)(2-70)+44.117-20) ⅔...
resLAZ), 207 him 12-201112) = Ей |
46) |
|
|
||
1920 |
2204112.)(2-70)+44. 17-20) ⅔... |
|
|
|
2 |
40 |
MAID 1.7- 440 |
4.) |
4470) |
- формула „фи-ти штрих 
Пример 111)-⅓
особые точки: 01420,
⅔ EK KEI
полюсы 1-го порядка Can =-та ≠о вточках и,
411)= 1: 414=432 4)Ддт?з: плюсы 1порядка) |
||
|
=-STEAK)--Снтк |
|
res(A),11=44) |
115 |
|
КЕК |
||
412) |
||
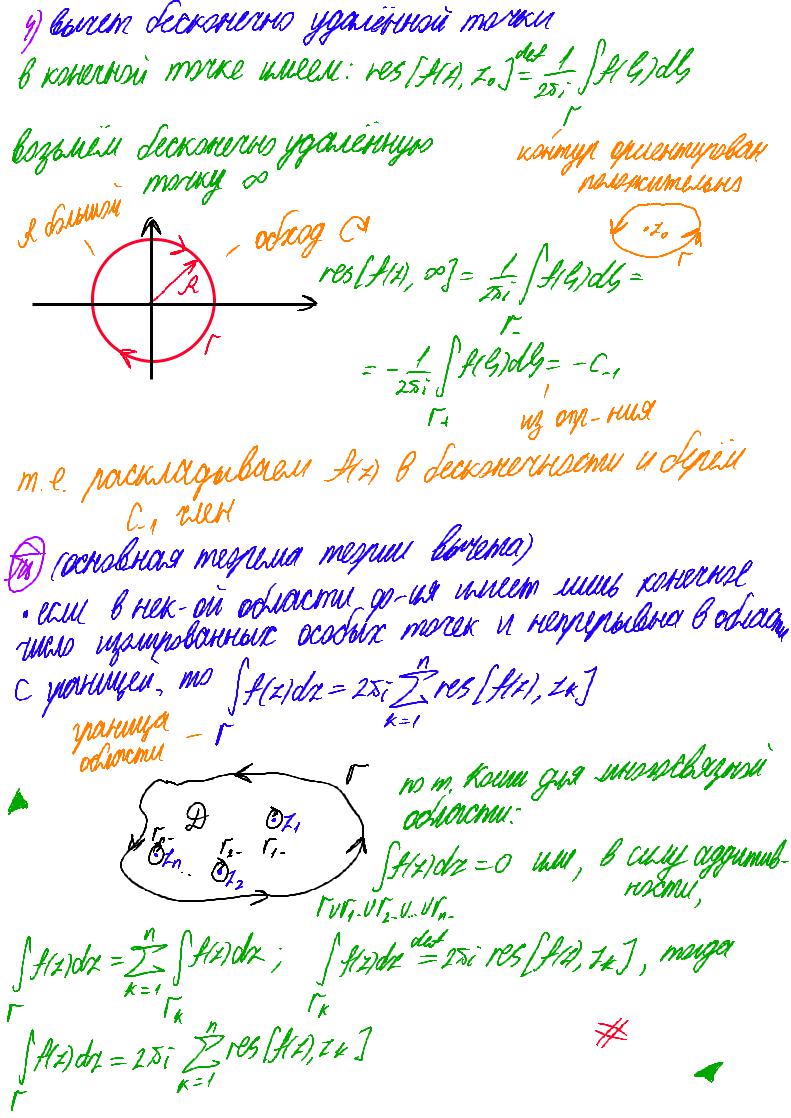
4)вычет бесконечно удалённой точки
вконечной точке имеем: resHa.173.Slides
возьмём бесконечноудалённую |
Г |
контур ориентирован |
|
- точку я |
положительно |
яблоки |
d |
|
- обхода |
• 7 |
|
|
|
r |
|||
|
|
|
>resltld.at#ifAlidb= |
||
|
|
|
|
||
T |
|
r |
-*fields|=-а, |
|
|
|
|
|
|||
|
|
|
|
||
|
|
|
те |
из апр-ния |
|
т.е. раскладываем Аа в бесконечности иберём С, член
(основная теорема теории вычета)
• если внекой области ф-ня имеет лишь конечное число изолированных особых точек и непрерывна вобласти
с границей, то / |
|
|
|
|||
|
Fdr 25,: [!resLAA,21 |
|||||
|
гранит-г |
|
|
|
|
|
|
области |
|
|
по т. Колтдля многосвязной |
||
|
|
|
|
|||
|
Д |
• Z |
|
области: |
|
|
|
"in Б- |
5- |
find-0 или, всилу аддитив |
|||
|
• |
|
|
|
|
|
|
" ½ |
|
|
|
ности, |
|
НкЁ!Hada; |
rur,-ur-v.ir.- |
|||||
|
||||||
ffndetwiresf1.LI, тогда |
||||||
Г |
|
|
Гк |
|
|
|
JAANE25T [НАМ,к] |
|
# |
||||
|
|
|||||
р |
к-1 |
|
|
|
|
|
0510 сумме |
вычетов, |
• 3712) |
чая во всей ¢,кроме конечного числа |
изолированных особыхточек:--тоже изолированная
особа точка,
сумма по всем
71
Г- 072
Б-
тогда ЁндАк),2к]-о
К-1
изолированным особым точкам, включая
1-х
по основной т
.:
On |
г /HIM =25:[MAN,к] |
|
Г- |
||
|
Г |
KII |
т.к. 2=0-тоже изолированная особя точка, то
resLAA,-I- Hack |
-Effendi |
|
|
г- |
|
Jude-/Had-willНАШ, 21=0 = |
||
r |
r |
|
|
Cation |
|
121=3 |
27-1 |
|
|
|
|
f (7+1) 'dL =-251m11, я] |
||
27-1 |
|
|
121=3 |
1) = 4¥? ¾ 11) |
|
|
||
получаем:ряд Ирана |
в к-начинается с ½ 141 |
|
резня,а]=-с, = + /4747251
121=3
Применение теории вычетов вдействительноманализе
• вычисление действительных определённых интегралов
вида д"Я(тx,canАх |
|
◦ вещ-наярациональнаяф-и |
dy-t.dz |
введём комплексную переменную 2- ein, drierне my-1"-е-"2- ½, „у = like-"= Let
й |
2T |
25 |
|
|
2 |
||
|
|
|
|
|
|
||
IRlsmx.mx/defR(Z;t,2iI)tE=2oiEresl1, 20 |
|||||||
|
|
|
|
|
й |
|
|
0 |
121=1 |
|
|
|
|
|
|
Пример / |
1 |
|
|
а >1 |
|
|
|
◦ наст М, |
|
|
|||||
%.-и'm-11 |
4-а |
2111 |
-f/attain |
than |
|||
22 / |
121=1422+6415 |
||||||
1 |
|||||||
О |
121=1 |
|
|
|
121=1 |
|
|
А
= ¾/анна = 255.741, к]
171=1 |
02722+9=0 |
внутри/И-1 только |
||||
4) = |
||||||
212 =-1115г |
7,=-11 Far |
|
||||
|
|
а |
|
а |
|
|
45ms/14,11] |
= 45 44=45 1 |
25 |
25 |
|||
|
|
|||||
|
| |
44 |
204+2 =421+1 |
1-02 |
||
|
|
|
|
|
||
полюс
1- и
порядка
Вычисление несобственных интегралов
"Imads, An допускает ан-кое продолжение на ¢, -а где имеета конечное число из-ных особых точек
/2) → • µ,/→ ◦, ННдт, 8-0 n 
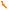
тогда"fhd-siiqresm.sn]-вверхней |
|
KII |
полуплоскости |
- У