1 / лаба 2

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное автономное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

КАФЕДРА №44

Институт вычислительных систем и программирования

ПРЕПОДАВАТЕЛЬ

Доцент				Бариков Л.Н.
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

Лабораторная работа №2

Операторы ветвления

по курсу: Основы алгоритмизации и программирования на C/C++

СТУДЕНТ ГР. №		Z0411				Карелина М. В.
	номер группы			подпись, дата		инициалы, фамилия

Номер зачётной книжки: 2020/3477

Санкт-Петербург

2021

Цель лабораторной работы: приобретение навыков структурного программирования на языке C/C++ при решении задач с использованием операторов ветвления if и switch.

Задание на программирование: используя технологию структурного программирования разработать программу для решения индивидуальной задачи по определению места нахождения точки с произвольно заданными координатами на координатной плоскости. В случае если точка попадает в одну их выделенных областей, программа должна определять площадь этой области по аналитической формуле.

При решении должны быть использованы условный оператор if и оператор-переключатель switch.

28.

Математическая модель (условия принадлежности точек выделенным областям и аналитическое определение площадей выделенных областей

М1:

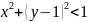
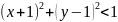
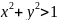
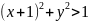
Площадь области М1:

Площадь квадрата 1х1- (Четверть круга – (сектор 600 - S треугольника)*2 – S треугольника)*2

1-((πr2/4) – (πr2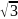/6 - /4)*2 - /4) )*2)=1-0.3424= ≈0,6576

М2:

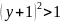
Площадь области М2:

Четверть круга – (сектор 60° - S треугольника)*2 – S треугольника =

= (πr²/4) – (πr²/6 - √3 /4)*2 - √3/4 = √3/4 - πr²/12=

= 0,433 – 0,2618 = ≈ 0.1712

М3:

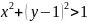
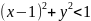
Площадь области М3:

Площадь области: половина круга (π/2) + площадь квадрата(1х1) - четверть круга = 1 + π/4 = 1.7854

М4:

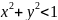
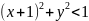
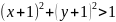
Площадь области М4:

(Четверть круга – (сектор 600 - S треугольника)*2 – S треугольника)*2= ((πr2/4) – (πr2/6 - /4)*2 - /4) *2)=(0.7854 – (0.5236-0.4330)*2 – 0.4330)*2=0.3424

М5:

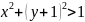
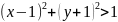
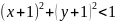
Площадь области M5:

Площадь области: единичный квадрат = 1х1=1

Схема алгоритма решения:

S1=1-((πr2/4) – (πr2/6 - /4)*2 - /4) )*2)

i

Конец

S5=1х1=1

S3=1 + π/4

S2=(πr²/4) – (πr²/6 - √3 /4)*2 - √3/4

I=1

I=2

I=3

I=5

I=4

(.) в М5

(.) в М4

(.) в М3

(.) в М2

(.) в М1

(.) вне зон

Начало

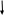
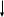
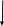
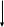
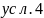
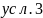
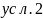
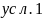
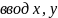
S4= ((πr2/4) – (πr2/6 - /4)*2 - /4) *2)

Текст программы:

#include<iostream>

#include<cstdlib>

#include<math.h>

#include<stdio.h>

#include<locale.h>

using namespace std;

int main()

{

double s1, s2, s3, s4, s5, x, y;

double M_PI = 3.1415926535;

setlocale(LC_ALL, "Russian");

int i = 0;

cout << "\ncoordination: x, y" << endl;

cin >> x >> y;

if ((x * x + (y - 1) * (y - 1) < 1) && ((x + 1) * (x + 1) + (y - 1) * (y - 1) < 1) && (x * x + y * y > 1) && ((x + 1) * (x + 1) + y * y > 1))

{

cout << "oblast' m1";

i = 1;

}

else if (((x + 1) * (x + 1) + y * y > 1) && ((y + 1) * (y + 1) > 1) && ((x + 1) * (x + 1) + (y - 1) * (y - 1) < 1))

{

cout << "oblast' m2";

i = 2;

}

else if ((x * x + y * y > 1) && (x * x + (y - 1) * (y - 1) > 1) && ((x - 1) * (x - 1) + y * y < 1))

{

cout << "oblast' m3";

i = 3;

}

else if ((x * x + y * y < 1) && ((x + 1) * (x + 1) + y * y < 1) && ((x + 1) * (x + 1) + (y + 1) * (y + 1) > 1) && (x * x + (y - 1) * (y - 1) > 1))

{

cout << "oblast' m4";

i = 4;

}

else if ((x * x + (y + 1) * (y + 1) < 1) && (x * x + y * y > 1) && ((x + 1) * (x + 1) + y * y > 1) && ((x + 1) * (x + 1) + (y + 1) * (y + 1) < 1) && ((x - 1) * (x - 1) + (y + 1) * (y + 1) > 1))

{

cout << "oblast' m5";

i = 5;

}

else cout << "point out the oblast'";

cout.precision(4);

switch (i)

{

case 1: cout << "S1=" << (s1 = 1 - ((M_PI / 4) - (M_PI / 6 - sqrt(3) / 4) * 2 - sqrt(3) / 4) * 2);

break;

case 2: cout << "S2=" << (s2 = (M_PI / 4) - (M_PI / 6 - sqrt(3) / 4) * 2 - sqrt(3) / 4);

break;

case 3: cout << "S3=" << (s3 = 1 + (M_PI / 4));

break;

case 4: cout << "S4=" << (s4 = ((M_PI / 4) - (M_PI / 6 - sqrt(3) / 4) * 2 - sqrt(3) / 4) * 2);

break;

case 5: cout << "S5=" << (s5 = 1);

}

cout << "\nrepeat - 1, exit - another" << endl;

cin >> i;

if (i == 1) main();

return 0;

}

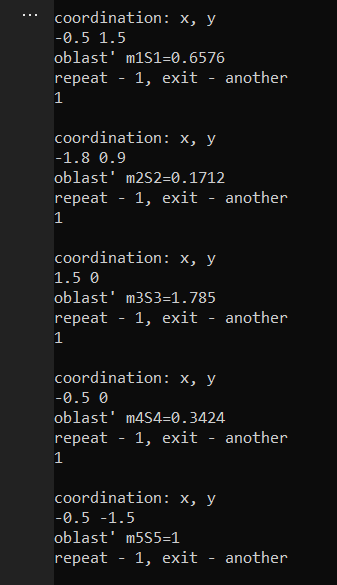
Скриншот результатов выполнения программы