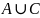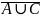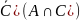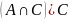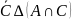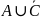KR2_Diskret_Karelina2
.docxМИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное автономное образовательное учреждение высшего образования
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»
КАФЕДРА №2
ПРЕПОДАВАТЕЛЬ
Доцент, с.н.с. |
|
|
|
В.И.Устимов |
должность, уч. степень, звание |
|
подпись, дата |
|
инициалы, фамилия |
КОНТРОЛЬНАЯ РАБОТА №1
по курсу: ДИСКРЕТНАЯ МАТЕМАТИКА
СТУДЕНТ ГР. № |
Z0411 |
|
|
|
М. В. Карелина |
|
|
номер группы |
|
подпись, дата |
|
инициалы, фамилия |
|
Санкт-Петербург 2022г.
Вариант №7
Задание 1.
Даны множества
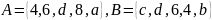 и универсальное множество
и универсальное множество
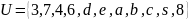 .
Построить следующие множества:
.
Построить следующие множества:
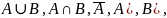
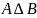 .
.
Объединение
множеств
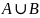 – это множество состоящее из элементов,
принадлежащих А или В. Исходя из этого,
множество
– это множество состоящее из элементов,
принадлежащих А или В. Исходя из этого,
множество
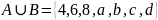 .
.
Пересечение
множеств
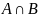 – это множество, состоящее из элементов,
принадлежащих одновременно обоим
множествам. Отсюда множество
– это множество, состоящее из элементов,
принадлежащих одновременно обоим
множествам. Отсюда множество
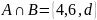 .
.
Дополнение множества
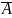 – это множество, состоящее из элементов,
принадлежащих универсуму и не принадлежащих
множеству A. Следовательно,
– это множество, состоящее из элементов,
принадлежащих универсуму и не принадлежащих
множеству A. Следовательно,
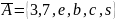 .
.
Разность множеств
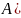 – это множество, состоящее из элементов,
принадлежащих множеству A и не принадлежащих
множеству B. Выходит
– это множество, состоящее из элементов,
принадлежащих множеству A и не принадлежащих
множеству B. Выходит
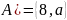 .
Разность множеств
.
Разность множеств
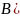 – это множество, состоящее из элементов,
принадлежащих множеству B и не принадлежащих
множеству A. Получаем
– это множество, состоящее из элементов,
принадлежащих множеству B и не принадлежащих
множеству A. Получаем
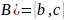 .
.
Симметрическая
разность множеств
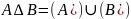 .
.
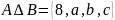 .
.
Задание 2.
Проверить равенство
множеств:
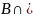 .
.
Для проверки, при помощи свойств операций над множествами, попытаемся упростить левую часть равенства.
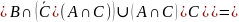
- свойство операции симметричной разности
Создадим таблицу принадлеежности для
A |
B |
C |
|
|
|
|
|
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
Создадим таблицу
для
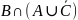 .
.
A |
B |
C |
B |
|
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
В итоге получаем 00100011= 00100011, следовательно равенство верно.
Задание 3.
Дано универсальное
множество
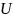 и три его подмножества
и три его подмножества
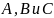 .
Известно, что
.
Известно, что
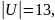
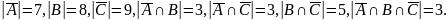
Найти
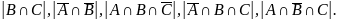
Для нахождения
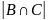 выполним
преобразования, используя свойства
операций над множествами:
выполним
преобразования, используя свойства
операций над множествами:
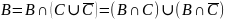
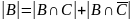 ,
отсюда
,
отсюда
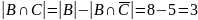
Аналогично найдем
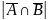 :
:
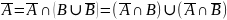
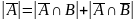 ,
отсюда
,
отсюда
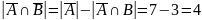
Найдем
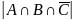 :
:
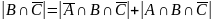 ,
отсюда
,
отсюда
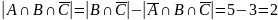
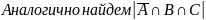 :
:
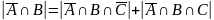 ,
отсюда
,
отсюда
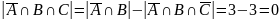
Найдем
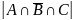 :
:
Выполним преобразования, используя де Моргана:

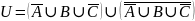
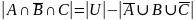
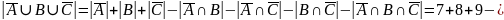
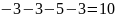
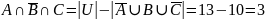
Задание 4.
Доказать равенство
множеств:
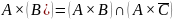 .
.
Рассмотрим левую
часть равенства:
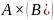 .
.
Согласно определению
декартова произведения двух множеств,
каждый элемент произведения представляет
собой упорядоченную пару
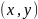 .
.
Пусть пара
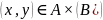 .
Тогда по определению декартова
произведения
.
Тогда по определению декартова
произведения
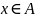 и
и
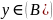 .
По определению разности множеств получим
и
.
По определению разности множеств получим
и
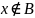 (значит
(значит
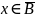 )
, а по определению пересечения получим
)
, а по определению пересечения получим
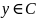 и
и
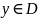 .
Следовательно, пара
.
Следовательно, пара
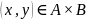 и
и
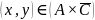 .
Тогда
.
Тогда
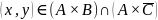 ,
что соответствует правой части равенства.
,
что соответствует правой части равенства.