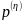Mat_TVMS
.docxМИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное автономное образовательное учреждение высшего образования
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»
КАФЕДРА №2
ПРЕПОДАВАТЕЛЬ
Доктор ф-м наук, профессор |
|
|
|
В.Г.Фарафонов |
должность, уч. степень, звание |
|
подпись, дата |
|
инициалы, фамилия |
КОНТРОЛЬНАЯ РАБОТА
по курсу:
ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
РАБОТУ ВЫПОЛНИЛА
СТУДЕНТ ГР. № |
Z0411 |
|
|
|
М. В. Карелина |
|||
|
номер группы |
|
подпись, дата |
|
инициалы, фамилия |
|||
Студенческий билет № |
2020/3477 |
|
|
|
||||
Санкт-Петербург 2022
Вариант №7
Задание 1.
Бросают
игральную кость. Путь событие А – это
выпадение четного числа, а событие В –
выпадение числа большего 4. Что представляют
собой события A , B,
![]() Какие элементы пространства элементарных
исходов данного опыта им благоприятствуют?
Какие элементы пространства элементарных
исходов данного опыта им благоприятствуют?
Решение:
Событие
 -
противоположно событию А, выпадение
нечетного числа, элементарные исходы
– 1, 3, 5.
-
противоположно событию А, выпадение
нечетного числа, элементарные исходы
– 1, 3, 5.
Событие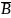 –
противоположно событию В, вероятное
выпадение чисел 1, 2, 3.
–
противоположно событию В, вероятное
выпадение чисел 1, 2, 3.
A∪B - выпадет то число, которое имеет хотя бы одно условие либо А либо В, выпадут все числа, кроме 2 и 4.
A∩B - выпадет число, которое имеет оба условия, то есть четное число больше четырёх, это 6.
A\B – происходит только событие А, выпадают только четные числа, элементарные исходы 2, 4, 6.
B\A – происходит только событие В, выпадают только числа больше 4, элементарные исходы 5 и 6.
Элементарные исходы – выпадение определенного количества очков на игральной кости: 1, 2, 3, 4, 5 или 6. Всего 6 элементарных исходов – полное пространство.
Задание 2.
Бросают две игральные кости. Найти вероятность события A, когда сумма выпавших очков равна 7, и события B, когда произведение выпавших очков равно 4.
Решение:
Для решения данной задачи будем использовать формулу:

где: |
p – вероятность события; m – число элементарных событий, благоприятствующих конкретному событию; n – общее число всевозможных исходов. |
Для нахождения n необходимо определить количество всех возможных комбинаций, которые могут выпасть на игральных костях. На каждой из игральных костей по шесть вариантов значений.
Следовательно,
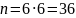 .
.
Для нахождения m рассмотрим необходимые сочетания чисел для каждого из событий.
Событие А.
Сумма
выпавших очков равная 7 возможна в случае
следующих комбинаций игральных костей:
(1 6),
(2
5),
(3
4),
(6
1),
(5
2),
(4
3).
6),
(2
5),
(3
4),
(6
1),
(5
2),
(4
3).
Отсюда
следует, что
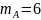 .
.
Событие В.
Произведение выпавших очков равное 4 возможно в случае следующих комбинаций игральных костей: (1×4), (2×2), (4×1).
Отсюда
следует, что
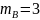 .
.
Воспользуемся формулой для определения вероятности для каждого из событий.
Вероятность
события А:
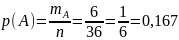 .
.
Вероятность
события B:
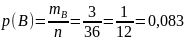 .
.
Ответ:
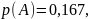
 .
.
Задание 3.
Случайным образом выбирают 3 шара из 10, среди которых 3 белых и 7 черных. Найти вероятность того, что среди выбранных окажется два белых шара.
Решение:
Общее
число шаров
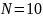 ;
;
Белых
шаров
 ;
;
Черных
шаров
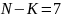 ;
;
Вынули
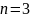 шаров;
шаров;
Событие
А вынуто
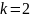 белых шаров;
белых шаров;
Событие
В вынуто
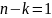 чёрных шаров.
чёрных шаров.
Для определения вероятности того, что среди трех вынутых шаров будут два белых будем определять по формуле:
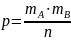
Для начала определим число всех элементарных событий, которое равно числу сочетаний из N элементов по числу вынутых шаров n.

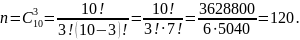
Далее
определим число элементарных событий
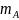 ,
благоприятствующих событию A, которое
равно числу сочетаний из К элементов
по числу вынутых шаров k:
,
благоприятствующих событию A, которое
равно числу сочетаний из К элементов
по числу вынутых шаров k:
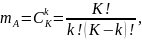
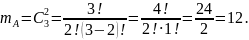
Аналогично
определим
число элементарных событий
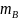 ,
благоприятствующих событию B:
,
благоприятствующих событию B:

Воспользуемся формулой для определения вероятности:

Ответ:
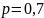 .
.
Задание 4.
Два независимых события A и B наступают с вероятностями 0,6 и 0,8 соответственно. Найти вероятность того, что наступит: а) хотя бы одно событие; б) ровно одно событие.
Решение:
Вероятность наступления события А или В (хотя бы одного из них) определяется по формуле:
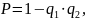
где
 тогда
тогда
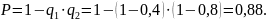
Вероятность наступления только одного из событий будет равна:
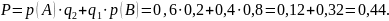
Ответ:
Задание 5.
В группе 20 студентов: 2 отличника, 4 хорошиста, 10 троечников и 4 двоечника. Отличники учат 100% экзаменационных билетов, хорошисты – только 80%, троечники – 60% и двоечники – только 40%. Найти вероятность того, что взятый наугад студент этой группы сдаст экзамен. Если некий студент данной группы сдал экзамен, то какова вероятность того, что он являлся одним из десяти троечников?
Решение:
Введём полную группу несовместных гипотез:
Н1 – случайный студент отличник;
Н2 – случайный студент хорошист;
Н3 – случайный студент троечник;
Н4 – случайный студент двоечник.
Определим вероятности этих несовместных гипотез:
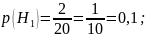
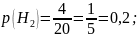
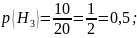
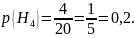
Определим условные вероятности события A (взятый наугад студент группы сдает экзамен):

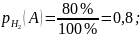
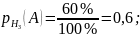

По формуле полной вероятности вычисляем вероятность события A:
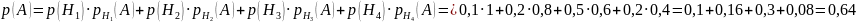
Далее, воспользовавшись формулой Байеса, определим вероятность того, что сдавший экзамен студент будет являться двоечником:


Ответ: 0,64 и 0,125.
Задание 6.
Известна вероятность события A: p(A) = 0,7. Дискретная случайная величина ξ – число появлений события A в трех опытах. Требуется построить ряд распределения этой случайной величины, найти ее математическое ожидание M[ξ], дисперсию D[ξ], среднее квадратическое отклонение σ и вероятность попадания в интервал p(|ξ – M[ξ]| < σ).
Решение:
Для построения ряда распределения случайной величины ξ необходимо найти все возможные значения ξ и соответствующие вероятности. Для этого воспользуемся формулой Бернулли:
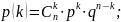
где: |
|
|
– число опытов; |
|
|
|
|
|
|
Подставим значения в формулу:
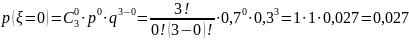

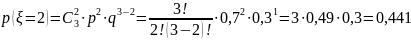
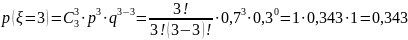
Построим ряд распределения случайной величины:
|
0 |
1 |
2 |
3 |
|
0,027 |
0,189 |
0,441 |
0,343 |
Математическое ожидание случайной величины определяется по формуле:

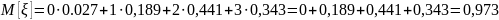
Дисперсию случайной величины определим по формуле:
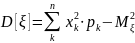

Среднее квадратическое отклонение случайной величины определяется как корень квадратный из дисперсии:
 .
.
Определим
вероятность попадания в интервал
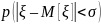 :
:
 .
.
Учитывая,
что функция Лапласа нечетная, т.е. Ф(-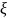 )
= -Ф(
),
получим:
)
= -Ф(
),
получим:
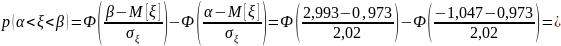

Ответ:
 ;
;

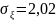 ;
;
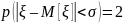 .
.
Задание 7.

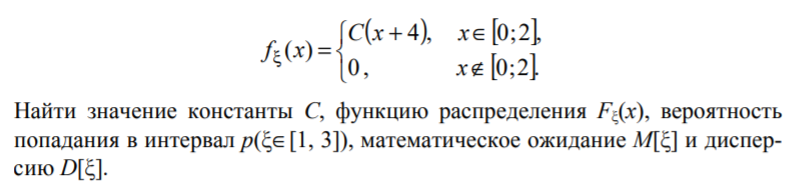 Решение:
Решение:

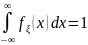
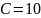
Следовательно:

Математическое ожидание:
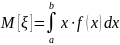
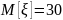
Дисперсия:

Ответ:
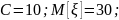
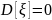 .
.
Задание 8.
Случайная величина ξ имеет нормальное распределение с математическим ожиданием a=15 и дисперсией σ 2 =400. Найти интервал, симметричный относительно математического ожидания, вероятность попадания в который равна p=0,9606.
Решение:
Если интервал является симметричным относительно математического ожидания, то формула имеет вид:
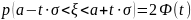
В данном случае:
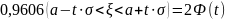
Отсюда:
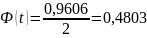
По
таблице значений функции Лапласа
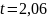 .
.
Теперь построим интервал:

Окончательно получим:
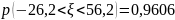
Ответ: интервал
Задание 9.
Дан ряд распределения двумерной случайной величины (ξ, η):

Найти значение p31, частные распределения случайных величин ξ и η, их математическое ожидание и дисперсию (т.е. M[ξ], D[ξ], M[η], D[η]), а также корреляционный момент Kξ,η и коэффициент корреляции rξ,η.
Решение:
Найдем
значение
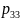 используя условие нормировки:
используя условие нормировки:

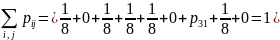
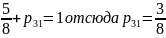
Следовательно, заданная таблица примет вид:
ξ η |
0 |
1 |
2 |
-1 |
1/8 |
0 |
1/8 |
0 |
1/8 |
1/8 |
0 |
1 |
3/8 |
1/8 |
0 |
Для нахождения частного распределения случайной величины ξ воспользуемся формулой:
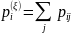
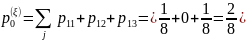
Аналогично найдем остальные значения и получим следующие частные распределения:
Ξ |
0 |
1 |
2 |
|
1/4 |
1/4 |
1/2 |
Далее найдем частные распределения случайной величин η по формуле:
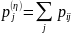

Получим следующие частные распределения:
η |
-1 |
0 |
1 |
|
5/8 |
1/4 |
1/8 |
Зная частные распределения лучайных величин, найдем математическое ожидание случайной величины ξ по формуле:
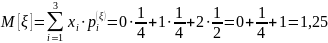
Аналогично найдем математическое ожидание случайной величины η:
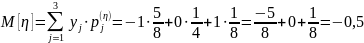
Найдем дисперсию случайной величины ξ используя полученное математическое ожидание:
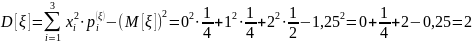
Найдем дисперсию случайной величины η:
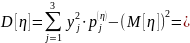
Среднее квадратическое отклонение случайной величины ξ:
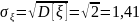
Среднее
квадратическое отклонение случайной
величины
 :
:

Корреляционный
момент
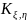 находится
по формуле:
находится
по формуле:
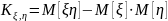
Для начала найдем математическое ожидание появления обоих событий:
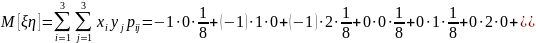
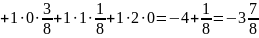 =
-3,875
=
-3,875
Теперь можно найти корреляционный момент:

Зная
корреляционный момент, найдем коэффициент
корреляции
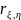 :
:
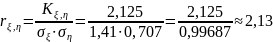
Ответ:
 ;
;
 ;
;
 ;
;
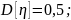
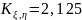 ;
;
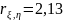 .
.

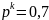 – вероятность
события А в одном опыте;
– вероятность
события А в одном опыте;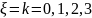 ;
;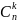 –
число
сочетаний;
–
число
сочетаний; –
вероятность
не наступления события А.
–
вероятность
не наступления события А.