практика / Практика Карелина

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное автономное образовательное учреждение высшего образования «САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

Кафедра 41

Институт информационных технологий и программирования

ОТЧЁТ ПО ПРАКТИКЕ ЗАЩИЩЁН С ОЦЕНКОЙ Руководитель
доц., канд. техн. наук, доц.				О. О. Жаринов
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЁТ ПО ПРАКТИКЕ

вид практики

Производственная практика

тип практики

Научно-исследовательская

на тему индивидуального задания

Изучение основ программирования

в среде Matlab

выполнен

Карелиной Марией Владимировной

по направлению подготовки

09.03.03

Прикладная информатика

код

наименование направления

09.03.03(01) Прикладная информатика в информационной сфере

наименование направления

направленности

код

наименование направленности

наименование направленности

Обучающийся группы №	Z0411		20.04.2023		М. В. Карелина
	номер		подпись, дата		инициалы, фамилия

Санкт–Петербург 2023

ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ

на прохождение производственной практики обучающегося направления подготовки/ специальности 09.03.03 Прикладная информатика

1. Фамилия, имя, отчество обучающегося: Карелина Мария Владимировна

2. Группа: Z0411

3. Тема индивидуального задания:

Изучение основ программирования в среде Matlab

4. Исходные данные:

1. методические указания по основам программирования в Matlab

2. задания для самостоятельного выполнения

5. Содержание отчетной документации:

5.1. индивидуальное задание;

5.2. отчёт, включающий в себя:

 титульный лист;

 результаты выполнения практических заданий по изучению основ программирования в среде Matlab;

 выводы по результатам практики;

 список использованных источников.

6. Срок представления отчета на кафедру: «22» апреля 2023 г.

Задание приняла к исполнению:

Обучающаяся 27.03.2023 М. В. Карелина

дата подпись инициалы, фамилия

Вариант 9.

Для выполнения данной практической работы в среде Matlab мною была выбрана онлайн версия на сайте https://uk.mathworks.com/products/matlab-online.html, требующая регистрации и предоставляющая 20 часов работы в месяц.

Интерфейс онлайн версии Matlab представлен на Рис. 1.

Рисунок 1. Интерфейc MatLab

Упражнение 1. Простейшие вычисления в Matlab

1. Вычислите значение выражения

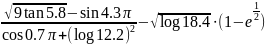
Для вычисления выражения необходимо ввести это выражение в командной строке и нажать Enter (Рис. 2).

(sqrt(9*tan(5.8)) – sin(4.3*pi))/(cos(0.7*pi)+(log(12.2))^2) – sqrt(log(18.4))*(1-exp(0.5))

Рисунок 2. Вычисление значения выражения

2. Найдите значения выражений, используя присвоение переменных

Чтобы найти значение выражения выше, можно, воспользовавшись присвоением переменных, значениям с дробями в выражении присвоить, a, b, c, x, и y. В результате, получим более простое выражение (Рис. 3):

a = cos(4.5*pi) / sin(8.5*pi);

b = tan(7.46) / cos(5.4*pi);

c = log(3.2) / (5*log(9.5));

x = cos(4.2*pi) / sin(7.6*pi);

y = sqrt(tan(7.58)/cos(5.4*pi));

(a^2-b+c)/(x+y)

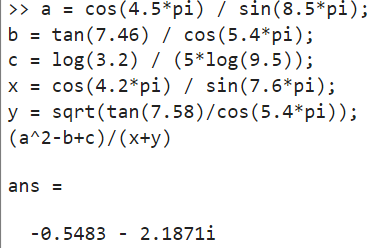
Рисунок 3. Вычисление значения выражения

Упражнение 2. Работа с массивами. Векторы-столбцы и векторы-строки.

1. Вычислить сумму векторов: ,

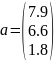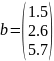
Для этого необходимо в командной строке ввести сначала вектор a. Используя квадратные скобки, и между значениями вектора поставить точку с запятой, а затем ввести вектор b таким же способом (Рис. 4):

a = [7.9;6.6;1.8];

b = [1.5;2.6;5.7];

c = a + b

Рисунок 4. Сложение векторов

2. Вывести второй элемент вектора-строки v  2.4 8.5 9.8 5.7 2.4 , заменить четвертый элемент вектора-строки на 2.7, записать в массив w первый, пятый и третий элементы.

Для вычислений векторов-строк необходимо записать их в командной строке также в квадратных скобках, но между значениями поставить запятые или пробелы.

Для того чтобы вывести лишь один элемент из вектора-столбца или вектора строки, необходимо написать его имя и далее в круглых скобках указать тот элемент, который необходимо вывести.

Если нам нужно заменить какой-то из элементов на другое значение, то необходимо после v(i) поставить знак присваивания и ввести новое значение.

Для помещения определенных элементов вектора в другой вектор в заданном порядке служит индексация при помощи вектора.

Операции с вектором-строкой и их результаты на Рис. 5.

v = [2.4,8.5,9.8,5.7,2.4];

v(2)

v(4) = 2.7

w = [v(1);v(5);v(3)]

Рисунок 5. Операции над вектором-строкой

3. В массиве вектора–строки w  5.8 2.4 3.3 4.5 9.8 3.7 2.9 заменить нулями элементы с третьего по седьмой, создать новый массив w1, используя элементы массива w со второго по пятый и составить массив w2, содержащий элементы w, кроме второго (используя сцепление строк).

Для обращения к блокам последовательно расположенных элементов вектора или вектора-строки служит индексация при помощи знака двоеточия.

Операции с вектором-строкой и их результаты на Рис. 6.

w = [5.8,2.4,3.3,4.5,9.8,3.7,2.9];

w(3:7) = 0

w1 = w(2:5)

w2 = [w(1) w(3:7)]

Рисунок 6. Операции над вектором-строкой

4. Перемножить элементы вектора-столбца 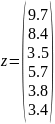, найти минимальный и максимальный элементы вектора z и индекс (порядковый номер) максимального элемента.

Перемножение элементов вектора-столбца или вектора-строки осуществляется при помощи функции prod.

Для нахождения минимума и максимума из элементов вектора служат встроенные функции min и max.

Вывод порядкового номера максимального элемента осуществляется при вызове функции max двумя выходными аргументами.

Операции над вектором-столбцом и их результаты на Рис. 7.

z = [9.7,8.4,3.5,5.7,3.8,3.4];

p = prod(z)

m = min(z)

M = max(z)

[M,ind] = max(z)

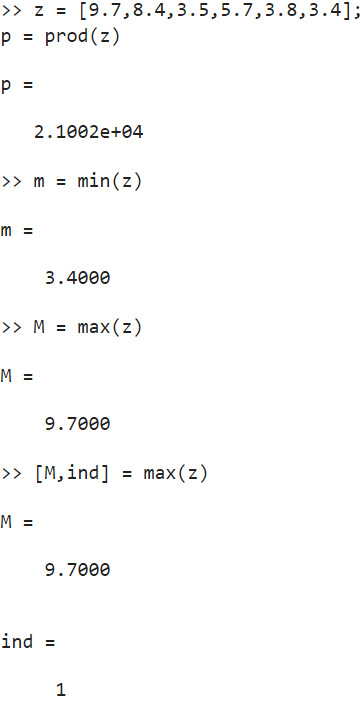
Рисунок 7. Операции над вектором-столбцом

5. Упорядочить вектор-строку r  5.7 4.2 1.4 1.7 7.4 0.5:

а) по возрастанию;

б) по убыванию;

в) в порядке возрастания их модулей;

г) по возрастанию с двумя выходными аргументами (это приведет к образованию массива индексов соответствия элементов упорядоченного и исходного массивов).

Функция упорядочения вектора по возрастанию его элементов sort следующая: R = sort(r)

Чтобы упорядочить вектор-строку по убыванию, необходимо функцию sort записать со знаком минус и также указать саму вектор-строку со знаком минус.

Упорядочение элементов в порядке возрастания их модулей производится с привлечением функции abs.

Упорядочение элементов по возрастанию с двумя выходными аргументами выглядит так: [rs,ind]=sort(r).

Операции над вектором-строкой на Рис. 8.

r = [-5.7 4.2 -1.4 1.7 7.4 0.5];

R = sort(r)

R1 = -sort(-r)

R2 = sort(abs(r))

[rs,ind] = sort(r)

Рисунок 8. Операции над вектором-строкой

6.

а) Перемножить вектор-строки v1 = (7 9 -1 2) и v2 = (–4 6 –3 1);

б) возвести во вторую степень вектор v1;

в) все элементы первого вектора v1 возвести в степень, равную соответствующим элементам второго вектора v2;

г) разделить вектор v1 на v2 и v2 на v1;

д) к вектору-строке v = (7 11 6 5) прибавить число 4.8, вычесть его из вектора, умножить вектор v на число 2 и разделить на это же число.

v1 = [7 9 -1 2];

v2 = [-4 6 -3 1];

u = v1.*v2

p = v1.^2

P = v1.^v2

d1 = v1./v2

d2 = v2./v1

v = [7 11 6 5];

s = v + 7.5

d = v - 7.5

M = v * 2

D = v / 2

Операции над векторами-строками и их результаты на Рис. 9-10.

Рисунок 9. Операции над двумя векторами-строками

Рисунок 10. Операции над вектором-строкой

Упражнение 3. Работа с функциями и графиками.

1. Выведите таблицу значений функции 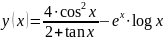в точках 0.1, 0.3, 0.4, 0.6, 1.3, 1.7, 2.5.

Вначале необходимо записать данные значения в вектор-строку x, а затем вычислить значения функции y(x) от каждой этой точки, поэтому необходимо в записи самой функции использовать поэлементные операции.

Таблица значений функции на Рис. 11.

x = [0.1 0.3 0.4 0.6 1.3 1.7 2.5];

y = (4 * cos(x).^2)/(2 + tan(x)) - exp(x).* log(x)

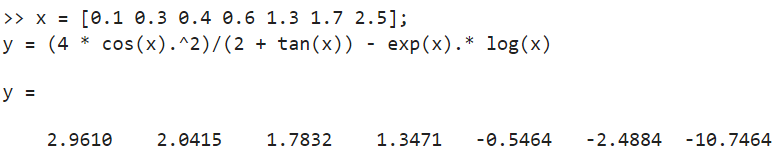
Рисунок 11. Таблица значений функции

2. Заполните вектор-столбец элементами, начинающимися с нуля и до единицы с шагом 0,2 (используя операцию транспонирование) и вектор-строку, начинающуюся с единицы до двух с шагом –0.3.

Результат на Рис. 12.

x = [0:0.2:1]'

y = [2:-0.5:1]

Рисунок 12. Заполнение вектор-столбца и вектор-строки элементами

3. Постройте график функции 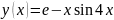на отрезке [0, 7].

Вывод отображения функции в виде графика состоит из следующих этапов:

• Задание вектора значений аргумента x.

• Вычисление вектора y значений функции y(x).

• Вызов команды plot для построения графика.

График функции и команды на Рис. 13.

x = [0:0.05:7];

y = exp(1) - x .* sin(4 * x);

plot(x, y)

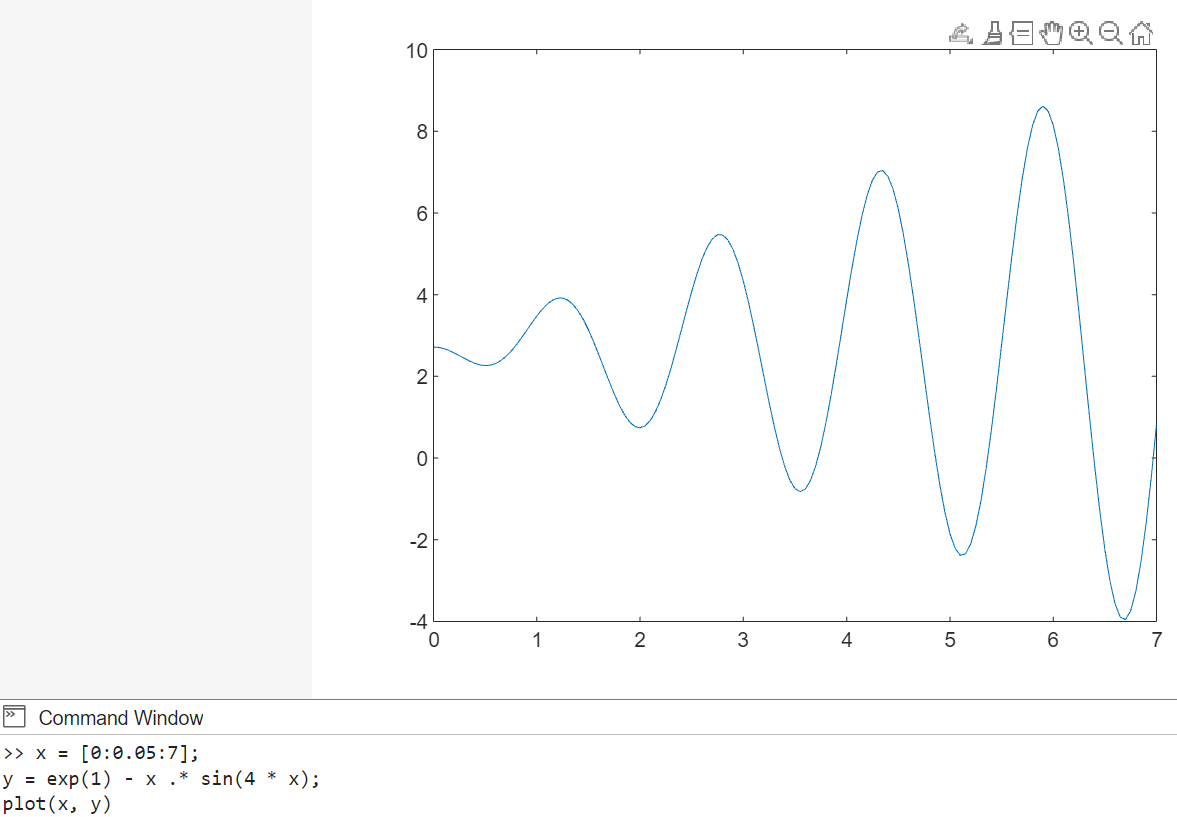
Рисунок 13. График функции

4. Постройте на отрезке [–5, –0,5] графики функций , .

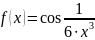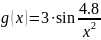График функций и команды на Рис. 14.

x = [-5:0.05:-0.5];

f = cos(1 ./ (6 .* x.^3));

g = 3 * sin(4.8 ./ x.^2);

plot(x,f,x,g)

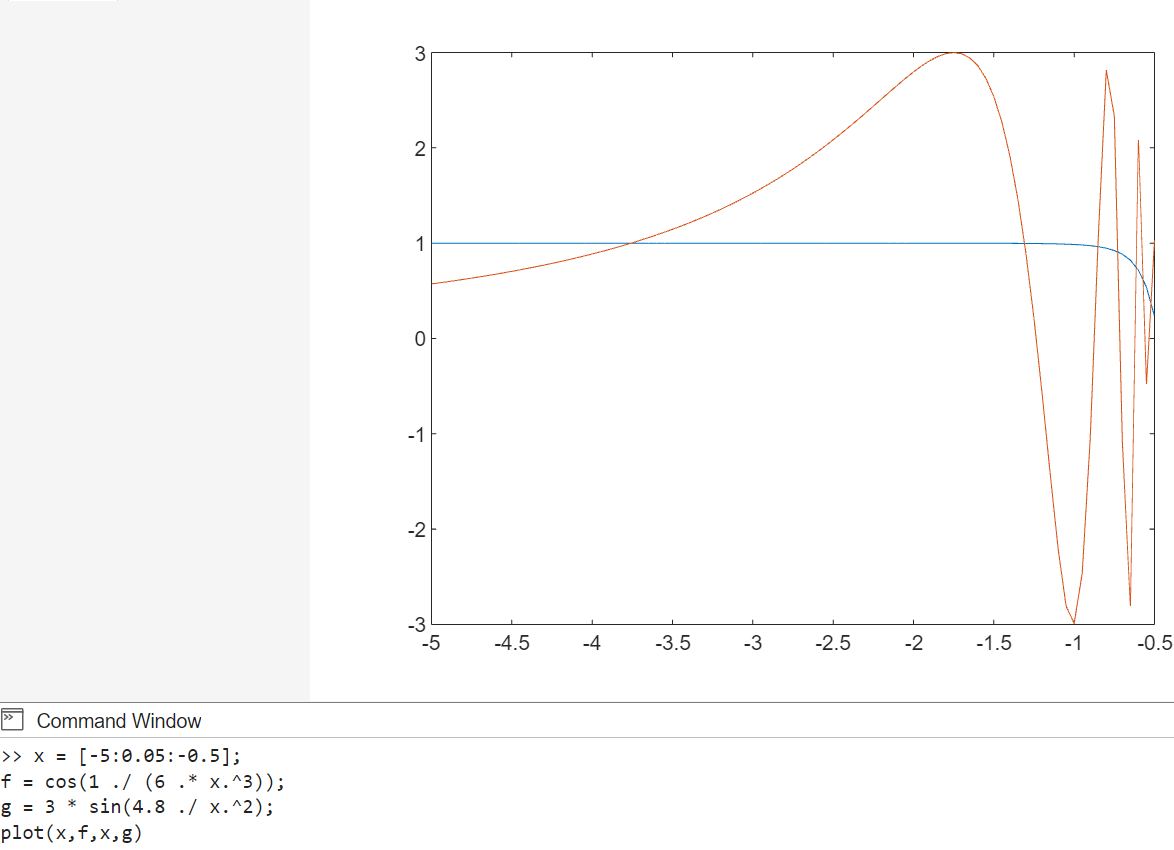
Рисунок 14. График функции

5. а) Найдите скалярное произведение векторов:

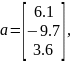
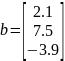
б) найдите длину (модуль) вектора a;

в) найдите векторное произведение векторов a и b.

a = [6.1;-9.7;3.6];

b = [2.1;7.5;-3.9];

S = dot(a,b)

A = length(a)

P = cross(a,b)

Операторы и результат на Рис. 15.

Рисунок 15. Операции с векторами

6. Найдите объем параллелепипеда, если

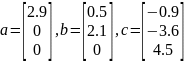
Операторы и результат на Рис. 16.

a = [2.9;0;0];

b = [0.5;2.1;0];

c = [-0.9;-3.6;4.5];

v = abs(sum(a .* cross(b,c)))

Рисунок 16. Объем параллелепипеда

Упражнение 4. Двумерные массивы и матрицы

1. а) Найдите сумму и разность матриц ,

;

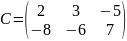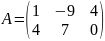б) умножьте матрицы С и ;

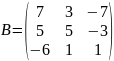в) полученную матрицу умножьте на 3.

Операции над матрицами и результат на Рис. 17.

C = [2 3 -5; -8 -6 7];

A = [1 -9 4; 4 7 0];

S = C + A

R = C - A

B = [7 3 -7; 5 5 -3; -6 1 1];

P = C * B

V = P * 3

Рисунок 17. Операции над матрицами

2. Найдите значение выражения

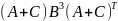
(A + C) * B^3 * (A + C)'

Операции над матрицами и результат на Рис. 18.

Рисунок 18. Выражение с матрицами

3. Вычислите выражение

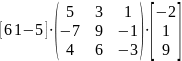
Операции над матрицами и результат на Рис. 19.

A = [6 2 -5];

B = [5 3 1; -7 9 -1; 4 6 -3];

C = [-2; 1; 9];

A * B * C

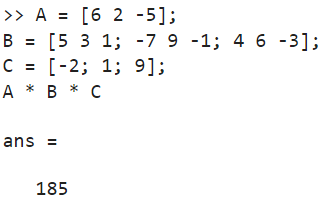
Рисунок 19. Операции над матрицами

4. Решите систему линейных уравнений

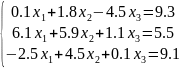
Решение системы уравнений на Рис. 20.

A = [0.1 1.8 -4.5; 6.1 5.9 1.1; -2.5 4.5 0.1];

b = [9.3;5.5;9.1];

x = inv(A) * b

Рисунок 20. Решение СЛАУ

5. Решите систему линейных уравнений № 4, матрица и вектор правой части которой хранятся в текстовых файлах matr.txt, rside.txt, и запишите результат в файл sol.txt.

Для начала создадим текстовые файлы matr.txt и rside.txt в которых хранятся матрица и вектор правой части. Данные должны быть записаны в файлы в следующем формате (Рис. 21).

Рисунок 21. Создание .txt файлов

Импортируем их в среду, перетащив в поле Files (Рис. 22).

Рисунок 22. Импорт файлов

Затем запишем данные из этих файлов в переменные, совершим операции над матрицами, а полученную матрицу экспортируем в файл sol.txt (Рис. 23).

A = readmatrix("matr.txt")

b = readmatrix("rside.txt")

x = inv(A) * b

writematrix(x, "sol.txt")

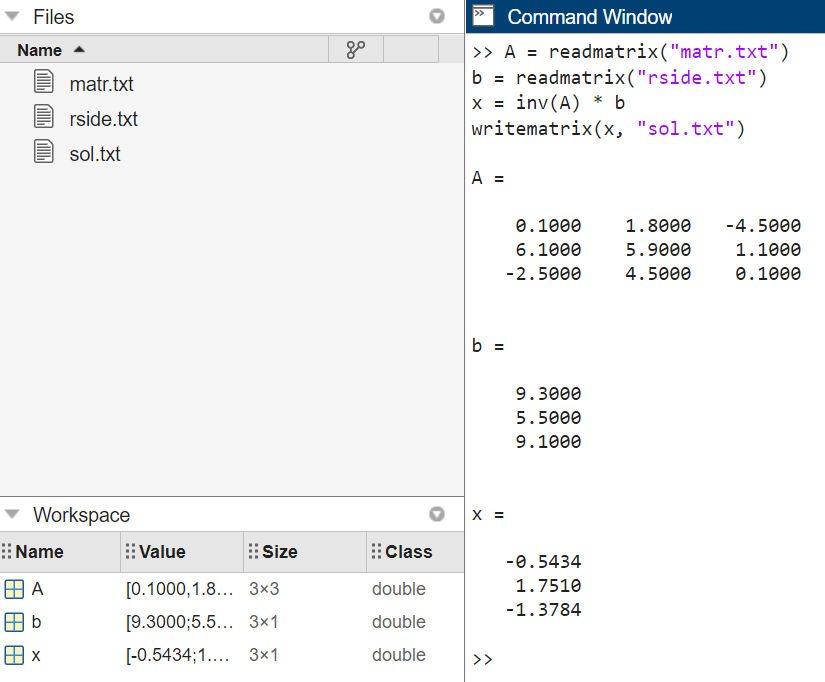
Рисунок 23. Операции с данными

Полученный файл на Рис. 24.

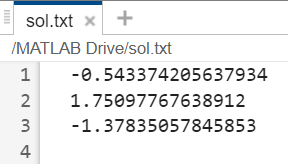
Рисунок 24. Файл sol.txt

Упражнение 5. Блочные матрицы.

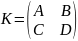
1. a) Введите четыре квадратные матрицы (A, B, C, D) размерностью два и создайте из них блочную матрицу

б) составьте блочную матрицу 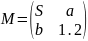, где

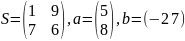
в) выделите блоки из полученной матрицы 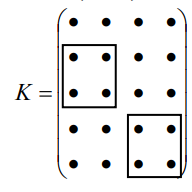и выделите 3-ю строку из матрицы М.

Работа с блочными матрицами на Рис. 25.

A = [1 9;2 8];

B = [3 7;4 6];

C = [5 5;6 4];

D = [7 3;8 2];

K = [A B;C D]

S = [1 9; 7 16];

a = [5;8];

b = [-2 7];

M = [S a; b 1.2]

K1 = K(1:2,1:2)

K2 = K(3:4,3:4)

m = M(3,:)

Рисунок 25. Работа с блочными матрицами

2. Удалите первую строку матрицы K и 3-ий столбец

K(1,:) = []

K(:,3) = []

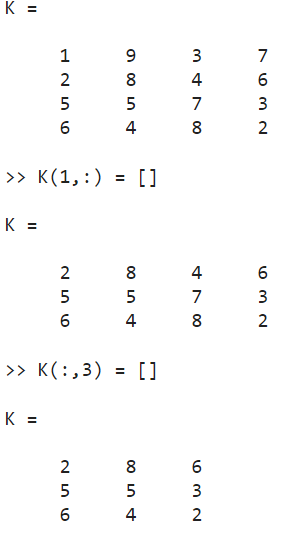
Рисунок 26. Удаление столбца и строки

3. а) Заполните прямоугольную и квадратную матрицу нулями, единицами и случайными числами при помощи индексации и встроенных функций;

б) заполните вектор-строку семью случайными числами;

в) создайте диагональную матрицу, у которой все внедиагональные элементы равны нулю.

Заполнение матриц на Рис. 27-29.

a)

A0(1:3,1:4) = 0

B0(1:3,1:3) = 0

A0  zeros3,4

B0  zeros3

A1(1:3,1:4) = 1

B1(1:3,1:3) = 1

A1 = ones(3,4)

B1 = ones(3)

Ar = rand(3,4)

Br = rand(3)

Рисунок 27. a)

б)

r = rand(1,7)

Рисунок 28. б)

в)

d  9;9;9;9;

D  diagd

Рисунок 29. в)

4. Заполните и запишите в файлы матрицы:

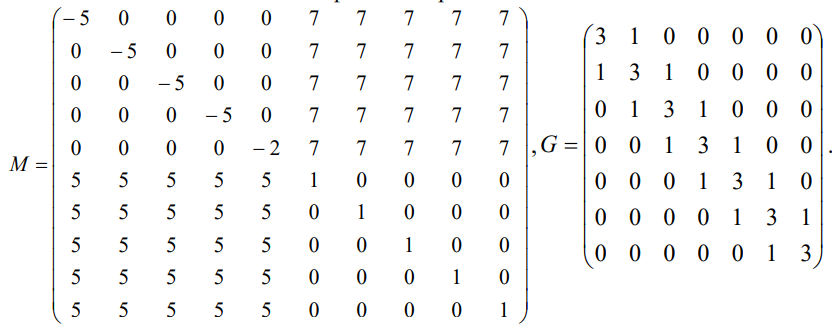
Заполнение матриц и их сохранение на Рис. 30.

M = [-5*eye(5) 7*ones(5); 5*ones(5) eye(5)];

M[5,5] = -2

save "M.txt" M -ascii

G = 3*eye(7)+diag(ones(1,6),1)+diag(ones(1,6),-1)

save "G.txt" G -ascii

Рисунок 30. Заполнение и сохранение матриц в файл

Упражнение 6. Визуализация матриц и поэлементные операции над ними.

1. В матрице М

а) вычислите сумму по столбцам и по строкам;

б) отсортируйте элементы этой матрицы в порядке возрастания их столбцов и строк;

в) вычислите максимальные и минимальные элементы в соответствующих столбцах матрицы М и строках:

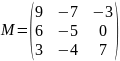
Операции над матрицей М на Рис. 31.

M = [9 -7 -3; 6 -5 0; 3 -4 7];

s = sum(M)

s2 = sum(M,2)

MC = sort(M)

MR = sort(M,2)

max1 = max(M)

min1 = min(M)

max2 = max(M,[],2)

min2 = min(M,[],2)

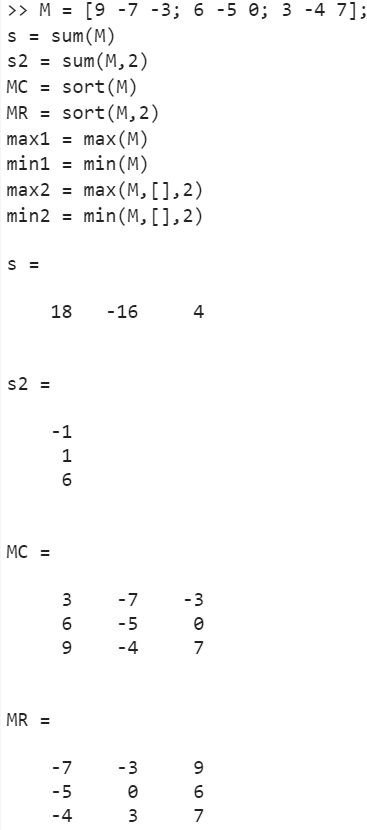
Рисунок 31. Операции над матрицами

2. Создайте квадратную матрицу A размера три, состоящую из случайных целых чисел от нуля до семи, вычтите из нее матрицу, состоящую из двоек, и введите необходимые выражения для вычисления норм полученной матрицы. Используйте полученную квадратную матрицу А. Вычислите приведенные ниже величины (нормы матрицы):

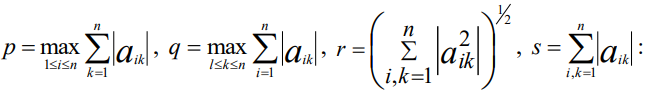
Создание матрицы и вычисление ее норм на Рис. 32.

A = round(7*rand(3))-2*ones(3)

p = max(sum(abs(A)))

q = norm(A, inf)

r = sqrt(sum(sum(abs(A).^2)))

s = sum(sum(abs(A)))

Рисунок 32. Вычисление норм матрицы

Упражнение 7. Графики, диаграммы и гистограммы.

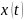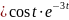1. Отобразите функц ю и на отрезке [–1, 1] в виде столбчатой диаграммы без промежутков.

Диаграмма на Рис. 33.

t = [-1:0.1:1];

x = cos(t).*exp(-3*t);

bar(t,x,1.0)

Рисунок 33. Столбчатая диаграмма

2. Напишите команды построения диаграммы с отдельным сектором, соответствующим минимальному значению среди элементов вектора, автоматически создав вспомогательный вектор. Используйте функции zeros для создания нулевого вектора той же длины, что x, и maxс двумя выходными аргументами для поиска номера минимального элемента в векторе x.

parts = zeros(size(data));

[mn,ind] = min(data);

parts(ind) = 1;

pie(data,parts)

Проверим на рандомных данных (Рис. 34)

data = [10;20;30;60;120];

Визуализация векторных данных может быть осуществлена при помощи pie3 и bar3, которые строят трехмерные круговые и столбчатые диаграммы, например команды (Рис. 35)

data = [20 30 70];

parts = [1 0 0];

pie3(data,parts)

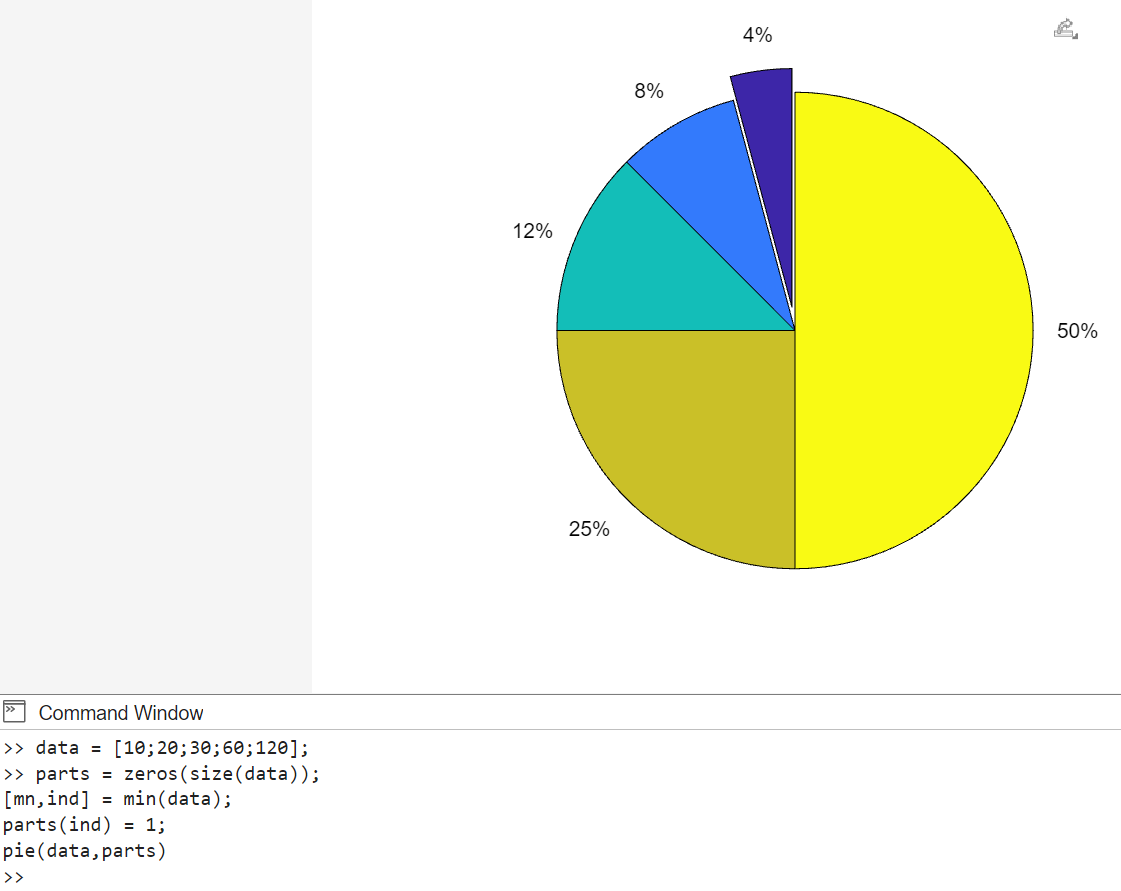
Рисунок 34. Круговая диаграмма с отдельным сектором

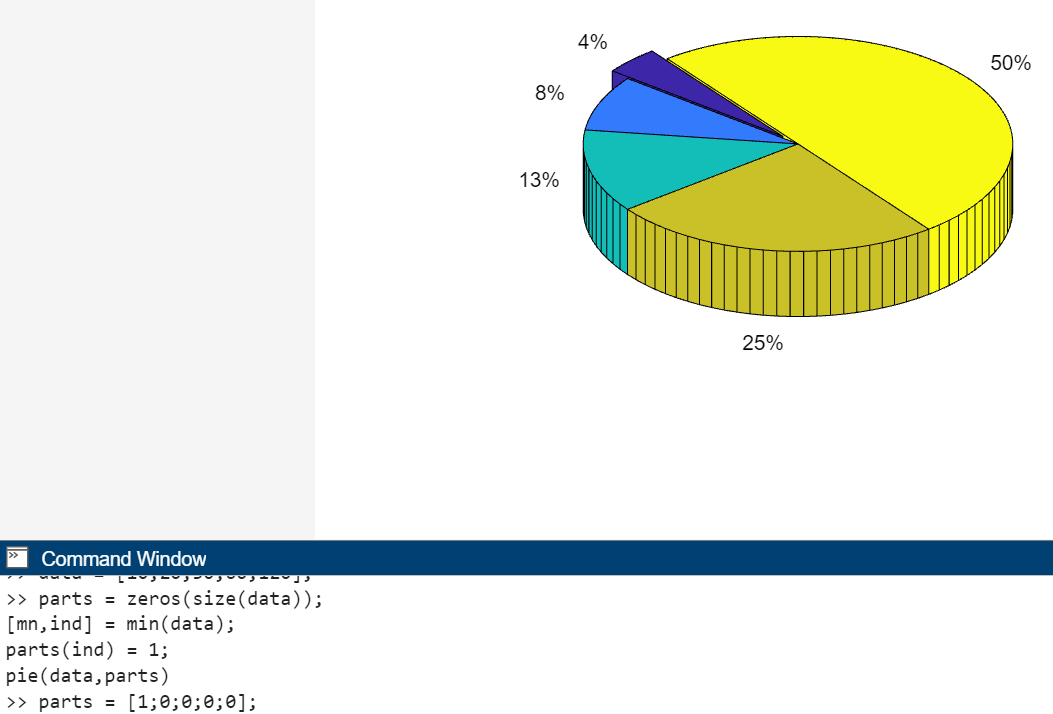
Рисунок 35. Трехмерная круговая диаграмма

3. Постройте диаграмму, где звездочки на горизонтальной оси будут отмечать центры интервалов.

Для увеличения числа интервалов следует в качестве второго аргумента указать число интервалов, например hist(data,50). Вместо автоматического разбиения на равные интервалы можно использовать собственное, задав вторым аргументом вектор, содержащий центры интервалов, что приводит к построению диаграммы, где звездочки на горизонтальной оси отмечают центры интервалов (Рис. 36).

data = [8 10 11 13 14 27 32];

centers = [10 25 30];

hist(data,centers)

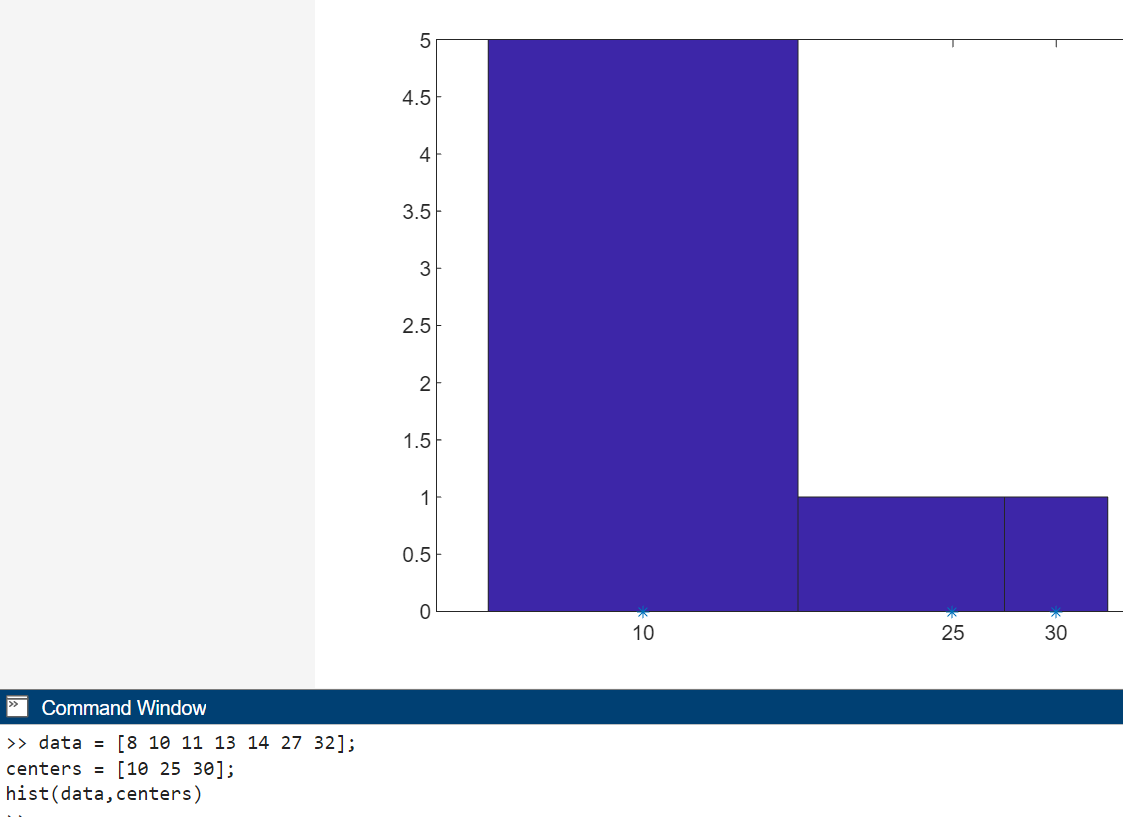
Рисунок 36. Центры интервалов

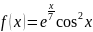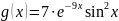4. Постройте графики и на отрезке [-2π, 2π]. Сгенерируйте вектор-строку значений аргумента x и вектор-строк f и g, содержащих значения функций.

Команда plot с двумя парами аргументов приводит к построению графика. Операторы и графики функций на Рис. 37.