моделирование

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное автономное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

Кафедра 41

ПРЕПОДАВАТЕЛЬ

Проф., д-р. техн. наук				А. П. Шепета
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

Контрольная работа

Парная регрессия и корреляция.

Вариант 7.

по курсу: Моделирование

СТУДЕНТКА ГР. №		Z0411		13.01.24		М. В. Карелина
	номер группы			подпись, дата		инициалы, фамилия

Номер студенческого билета: 2020/3477

Санкт-Петербург

2024

Вариант 7.

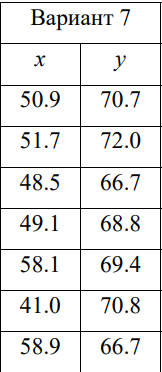
1. Для характеристики зависимости y от x рассчитать параметры линейной регрессии.

2. Оценить полученную модель регрессии через среднюю ошибку аппроксимации, коэффициент детерминации и F- критерий Фишера.

Заполним таблицу:

								Ai
1	50.9	70.7	3598,63	2590,81	4998,49	69,3585	1,341496	1,897449
2	51.7	72.0	3722,4	2672,89	5184	69,20249	2,797506	3,885425
3	48.5	66.7	3234,95	2352,25	4448,89	69,82653	-3,12653	4,687456
4	49.1	68.8	3378,08	2410,81	4733,44	69,70953	-0,90953	1,321985
5	58.1	69.4	4032,14	3375,61	4816,36	67,95441	1,445585	2,082976
6	41.0	70.8	2902,8	1681	5012,64	71,28913	-0,48913	0,690856
7	58.9	66.7	3928,63	3469,21	4448,89	67,7984	-1,0984	1,646784
Итого	358,2	485,1	24797,63	18552,58	33642,71	485,139	-0,039	16,21293
Средн.	51,1714	69,3	3542,519	2650,369	4806,101	69,30557
	5,64388779	1,900376
	31,85346939	3,611429

Посчитаем .

Среднее квадратическое отклонение рассчитаем по формуле:

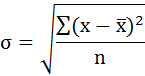
Внесем в таблицу среднее квадратическое отклонение для x и y.

Возведя в квадрат полученное значение получим дисперсию D или ².

Для расчёта параметров линейной регрессии

 

Параметры уравнения можно определить по формулам:

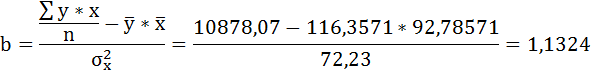
b = -0,195

a = 79,285

Таким образом, уравнение регрессии:

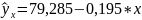
С увеличением фактора х на 1 ус.ед. результативный признак снижается в среднем на 0,195 ус. ед. Тесноту линейной связи оценит коэффициент корреляции:

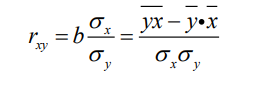
= -0,579

Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:

0.1 < rxy < 0.3: слабая;

0.3 < rxy < 0.5: умеренная;

0.5 < rxy < 0.7: заметная;

0.7 < rxy < 0.9: высокая;

0.9 < rxy < 1: весьма высокая;

Т.к. значение коэффициента корреляции меньше 0,3, в нашем примере связь между признаком у и фактором х слабая и обратная (с увеличением х показатель у уменьшается).

Оценку качества построенной модели регрессии дает коэффициент детерминации, равный квадрату коэффициента корреляции. Коэффициент детерминации (R²) характеризует долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака y.

= 0,335

Т.е. в 33,5% случаев изменения х приводят к изменению y. Другими словами - точность подбора уравнения регрессии -умеренная. Остальные 66,5% изменения у объясняются факторами, не учтенными в модели (а также ошибками спецификации).

33,5% вариации показателя y объясняется вариацией фактора x.

Качество модели также определяет средняя ошибка аппроксимации:

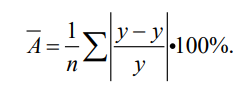
= 2,316133%

Качество построенной модели оценивается как хорошее, так как 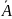не превышает 8-10%.

Средний коэффициент эластичности Э показывает, на сколько процентов в среднем по совокупности изменится результат y от своей средней величины при изменении фактора x на 1% от своего среднего значения:

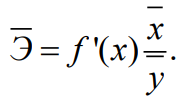
=-0,144

Увеличение фактора х (от своего среднего значения) на 1% снижает в среднем результативный признак на 0,144%. 4 Оценку значимости уравнения регрессии в целом проведем с помощью F -критерия Фишера. Фактическое значение F -критерия:

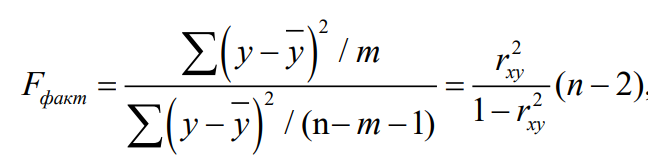
= 2,523662

Табличное значение критерия при пятипроцентном уровне значимости и степенях свободы =1, =7-5=2, составляет табл = 6.61. Так как, = 2,524 < = 6.61 то уравнение регрессии признается статистически не значимым.

Общие расчеты в программной среде Excel представлены на Рисунке 1.

Рисунок 1 - Расчет в Excel