сои

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное автономное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

Кафедра 41

ПРЕПОДАВАТЕЛЬ

Доцент, физ.-мат. наук				Е. А. Яковлева
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

Контрольная работа

по курсу:  

Статистическая обработка информации

СТУДЕНТКА ГР. №		Z0411		19.01.24		М. В. Карелина
	номер группы			подпись, дата		инициалы, фамилия

Номер студенческого билета: 2020/3477

Санкт-Петербург

2024

Имеются следующие выборочные данные (выборка 10%-ная, механическая) о выпуске продукции и сумме прибыли, млн. руб. В соответствии с вариантом n=2, m=7. Результат представлен в таблице 1.

Таблица1

№ предприя-тия	Выпуск продукции	Прибыль	№ предприятия	Выпуск продукции	Прибыль
1	62	15,7	16	52,0	14,6
2	78,0	18,0	17	62,0	14,8
3	41,0	12,1	18	69,0	16,1
4	54,0	13,8	19	85,0	16,7
5	62	15,5	20	72	15,8
6	34	19	21	71,0	16,4
7	45,0	12,8	22	44	29
8	57,0	14,2	23	72,0	16,5
9	67,0	15,9	24	88,0	18,5
10	82	17,6	25	72	16,4
11	92,0	18,2	26	74,0	16,0
12	48,0	14	27	96,0	19,1
13	59,0	16,5	28	75,0	16,3
14	68,0	16,2	29	101,0	19,6
15	82	16,7	30	72	17,2

По исходным данным:

1. Постройте статистический ряд распределения предприятий по сумме прибыли, образовав пять групп с равными интервалами. Постройте графики ряда распределения.

2. Определите границы, в которых с вероятностью 0,997 заключена сумма прибыли одного предприятия в генеральной совокупности.

3. Используя χ2 -критерий Пирсона, при уровне значимости α=0,05 проверить гипотезу о том, что случайная величина X – сумма прибыли – распределена по нормальному закону.

4. Установите наличие и характер корреляционной связи между стоимостью произведённой продукции (X) и суммой прибыли на одно предприятие (Y). Постройте диаграмму рассеяния и линию регрессии.

5. Определите коэффициенты выборочного уравнения регрессии

6. Рассчитайте линейный коэффициент корреляции. Используя t-критерий Стьюдента, проверьте значимость коэффициента корреляции. Сделайте вывод о тесноте связи между факторами X и Y, используя шкалу Чеддока.

1. Постройте статистический ряд распределения предприятий по сумме прибыли, образовав пять групп с равными интервалами. Постройте графики ряда распределения.

В программе Excel заполняется таблица исходных данных и выполняется сортировка третьего столбца (прибыль) в порядке возрастания. В результате получается новый интервальный ранжированный ряд (Рис. 1). Имеются следующие выборочные данные (выборка 10%-ная, механическая) о выпуске продукции и сумме прибыли, млн. руб.:

Рисунок 1 - Сортировка данных по столбцу Прибыль

Дискретный вариационный ряд разбивается на интервалы, число которых подсчитывается по формуле Стержесса:

, где N – количество измерений, то есть 30

k = 5,85, получаем 7 групп.

Длина частичного интервала определяется по формуле

Размах = 

Медиану нашли по значению по середине таблицы. При этом на середине лежало 2 числа: 16,2 и 16,3. В этом случае их сложим их и разделим на 2.

Мода – в результатах встречается 3 раза повторяющиеся значения по 2 раза (3 дублета).

Результат выполнения расчетов (Рис. 2).

Рисунок 1 – Результат расчётов

Значение прибыли 29 отнесем к выбросу, тогда Тогда x_min = 12,10, x_max = 19,60, среднее значение = 16,64

Определим границы интервалов (Рис. 3).

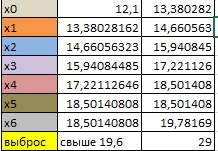
Рисунок 3 – Таблица границ интервалов

Результат группировки представлен на рисунке 4.

Рисунок 4 – Результат группировки

Подсчитывается количество предприятий, принадлежащих каждому из интервалов. Вычисляются накопленная частота и середина интервала. Результат представлен на рисунке 5.

Рисунок 5 – Статистический ряд распределения предприятий

По данной таблице построим следующие графики (рис.6-8)

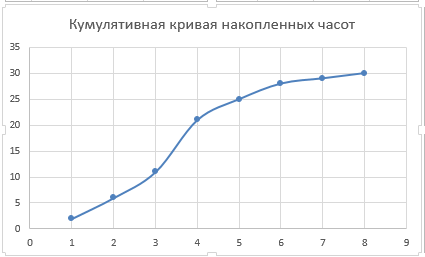
Рисунок 6 – Кривая ненормированной плотности распределения

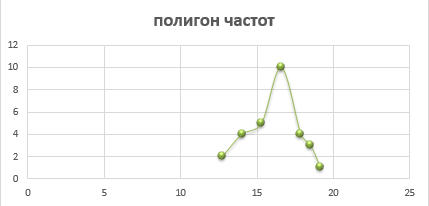
Рисунок 7 – Полигон частот

Рисунок 8 – Гистограмма

2. Определите границы, в которых с вероятностью 0,997 заключена сумма прибыли одного предприятия в генеральной совокупности. Границы для среднего найдем из соотношения:

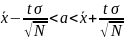
Для вероятности 0,997 коэффициент доверия равен 3.

3. Используя χ2-критерий Пирсона, при уровне значимости α=0,05 проверил гипотезу о том, что случайная величина X – сумма прибыли – распределена по нормальному закону.

Сначала рассчитаем среднее значение сгруппированного ряда, дисперсию и среднее квадратичное отклонение.

Среднее значение сгруппированного ряда

 

Дисперсия

   

Среднее квадратичное отклонение

 

Результат расчётов представлен ниже (Табл. 2):

Таблица 2 - Среднее значение, дисперсия и среднеквадратическое отклонение

Среднее значение	Дисперсия	Сигма
16,01354	3,87177	1,96768

Опираясь на данные сведения, вычислим следующие характеристики:

•    , где    и σ = 2,638;

• функция Гаусса: ;

•  , где N = 30 и h = 1,3;

•    .

Получим таблицу, представленную на рисунке 9.

Рисунок 9 – Таблица для проверки распределения по нормальному закону

Сравним полученные результаты с теоретическими, используя критерий Пирсона:

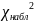 . = 4,35

По таблице критических точек распределения χ² по уровню значимости α = 0,05 и числу степеней свободы k = 7 - 2 - 1 = 2, находим χ²_кр = 14,1.

Так как:

χ²_набл = 4,35,

χ²_кр = 14,1,

χ²_набл <χ²_кр

Получается, что, гипотеза о нормальном распределении не отклоняется.

4. Установите наличие и характер корреляционной связи между стоимостью произведённой продукции (X) и суммой прибыли на одно предприятие (Y). Постройте диаграмму рассеяния и линию регрессии.

Используя изначальные данные для 1-го задания – отсортируем значения по выпуске продукции и обозначим их за x, прибыль обозначим за y.

С помощью стандартной надстройки Excel «Анализ данных» построим точечную диаграмму по x и y, построим линейную линию тренда, включим показ уравнения на диаграмме и поместим на диаграмму коэффициент детерминации (R²). Результат представлен на Рис. 10.

Рисунок 10 - Поле корреляции

Получилось выборочное уравнение регрессии:

y= 0,0342x + 14,319.

R²= 0,0371.

Коэффициент детерминации показывает, какая доля дисперсии результативного признака объясняется влиянием независимых переменных.

Коэффициент детерминации получился довольно слабым. Для того чтобы улучшить результаты удалим сильно отдалённые результаты от линии тренда – так называемые «выбросы», которые портят график. Результат на рисунке 11.

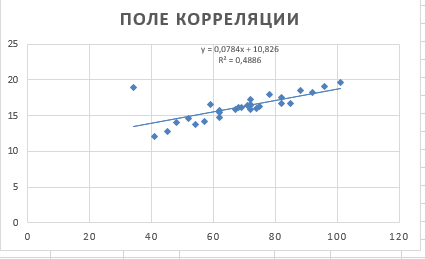
Рисунок 11 – Поле корреляции после удаления выбросов

Теперь выборочное уравнение регрессии:

y = 0,0784x + 10,826.

Коэффициент детерминации R²=0,4886.

Коэффициент детерминации объясняет 48,9% переменных, объясняемые рассматриваемым уравнением.

Коэффициент детерминации объясняет 48,9% переменных, объясняемые рассматриваемым уравнением, то есть 48,9% вариации показателя y объясняется вариацией фактора x.

Остальные 51,1% изменения у объясняются факторами, не учтенными в модели (а также ошибками спецификации).

5. Определите коэффициенты выборочного уравнения регрессии

a = 10,8401

b = 0,0782

Уравнение регрессии имеет следующий вид

y = 0,0782x+10,8401

Параметры уравнения также можно определить по формулам:

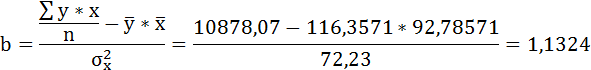
6. Рассчитайте линейный коэффициент корреляции. Используя t-критерий Стьюдента, проверьте значимость коэффициента корреляции. Сделайте вывод о тесноте связи между факторами X и Y, используя шкалу Чеддока.

Тесноту линейной связи оценит коэффициент корреляции:

Или же

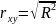
0,485802

Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:

0.1 < r_xy < 0.3: слабая;

0.3 < r_xy < 0.5: умеренная;

0.5 < r_xy < 0.7: заметная;

0.7 < r_xy < 0.9: высокая;

0.9 < r_xy < 1: весьма высокая;

Таким образом, линейная связь между выпуском продукции и величиной прибыли умеренная.

Качество модели также определяет средняя ошибка аппроксимации:

= 4,7%

Качество построенной модели оценивается как хорошее, так как 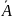не превышает 8-10%.

Средний коэффициент эластичности Э показывает, на сколько процентов в среднем по совокупности изменится результат y от своей средней величины при изменении фактора x на 1% от своего среднего значения:

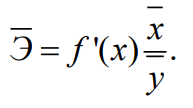
= 0,331%

Увеличение фактора х (от своего среднего значения) на 1% снижает в среднем результативный признак на 0,331%.

Оценку значимости уравнения регрессии в целом проведем с помощью F -критерия Фишера. Фактическое значение F -критерия:

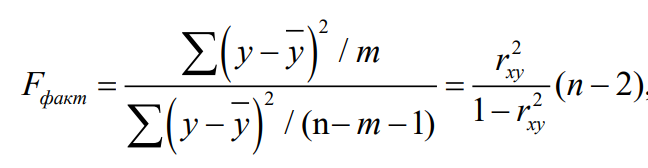
= 26,454

Табличное значение критерия при пятипроцентном уровне значимости и степенях свободы =1, =30-2=28, составляет табл = 2,53. Так как, = 26,454> = 2,53 то уравнение регрессии признается статистически значимым, надежным.

Благодаря вычислительным возможностям функции Анализ данных, в программе Excel были найдены предсказанные значения   и остатки (y- ). На основе этих сведений были построены следующие графики (Рис. 12-13):

Рисунок 12 - Распределение заданных значений y и предсказанных значений

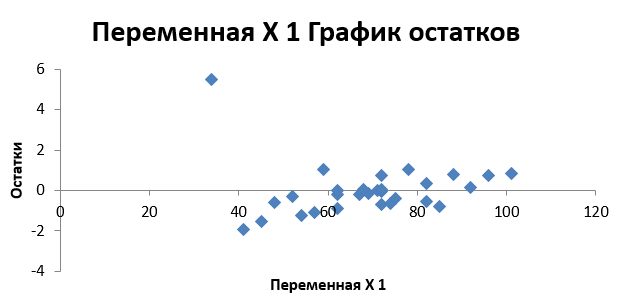
Рисунок 13 - Распределение остаточных значений (y- )

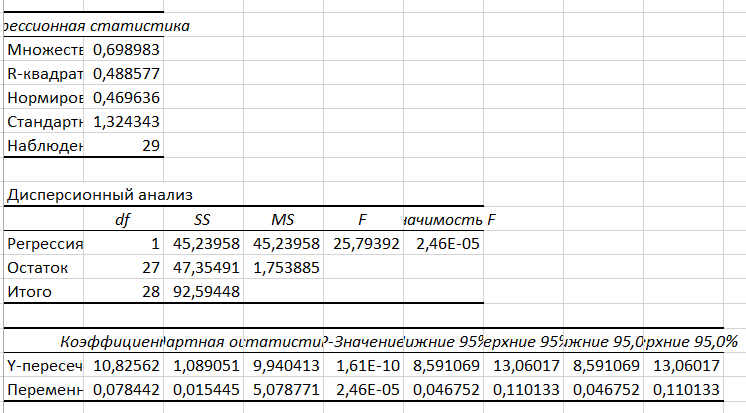
Рисунок 13 - Вывод итогов регрессии

Коэффициент a является достоверным, если он лежит в промежутке (8,591069, 13,06017).

Коэффициент b является достоверным, если он лежит в промежутке (0,046752, 0,110133).

Оценку статистической значимости параметров регрессии проведем с помощью t-статистики Стьюдента.

Табличное значение t-критерия составит t_табл = 2,045.

Определим случайные ошибки m_a, m_b, m_rxy (Табл. 3):

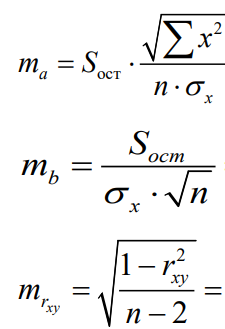
Таблица 3 - Случайные ошибки

ma	61,51601809
mb	0,01152054
mrxy	0,13551457

Тогда, , ,

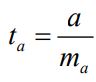Фактические значения t-статистики представлены в Табл. 4.

Таблица 4 - Фактические значения t-статистики

ta	0,1762164
tb	6,7895452
trxy	5,1433234
	26,4537758

Фактическое значение t-статистики не превосходит табличное значение: t_a< t_табл поэтому параметр a статистически не значим.

Фактические значения t-статистики превосходят табличное значение: t_b >t_табл , t_rxy >t_табл поэтому параметр b и коэффициент корреляции статистически значимы.

Найдём расчетную величину средней ошибки аппроксимации E, значение очень малое, что свидетельствует о хорошо проработанной модели уравнения. Также посмотрим вывод остатка (Рис. 14).

Рисунок 14 – Вывод остатка

Вывод

В заключение следует отметить, что задача по анализу данных о прибыли выборки из 30 предприятий с помощью программы Excel и статистических методов была выполнена. Данные были отсортированы, определены частоты и интервалы, рассчитаны различные статистические показатели, такие как диапазон, среднее, медиана и мода.

Гипотеза о нормальном распределении данных была проверена с помощью χ2-критерия Пирсона, и она была признана удовлетворительной при уровне значимости α = 0,05. χ²_набл < χ²_кр

Также были рассчитаны среднее значение, дисперсия и стандартное отклонение сгруппированных данных.

Корреляция между стоимостью продукции и прибылью также была определена как положительная и сильная, т.к. график растёт и коэффициент корреляции r=0,933 что указывает на весьма сильную связь между этими двумя переменными.

Уравнение регрессии: y = 0,0782x+10,8401.

В конечном итоге, задача была успешно решена, поскольку был проведен тщательный анализ данных о прибыли по выборке предприятий.