мо

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное автономное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

ИНСТИТУТ НЕПРЕРЫВНОГО И ДИСТАНЦИОННОГО ОБРАЗОВАНИЯ

Кафедра 41

ПРЕПОДАВАТЕЛЬ

Профессор, д-р техн. наук				Т. М. Татарникова
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

Лабораторная работа №1

Кластеризация данных

по курсу: Машинное обучение

СТУДЕНТКА ГР. №		Z0411		21.05.24		М. В. Карелина
	номер группы			подпись, дата		инициалы, фамилия

Номер студенческого билета: 2020/3477

Санкт-Петербург

2024

Цель работы:

изучить алгоритмы и методы кластерного анализа на практике.

Порядок выполнения

1. Получить у преподавателя набор данных для проведения кластерного анализа, при необходимости провести нормализацию и кодирование данных.

2. Провести предварительную обработку данных.

3. Выполнить кластеризацию объектов

иерархическим агломеративным методом

• выбрать подходящую метрику расстояния;

• построить дендрограмму;

• рассчитать оптимальное число кластеров.

методом k-средних.

• задать число кластеров;

• рассчитать евклидово расстояние между кластерами;

• определить объекты, относящиеся к каждому кластеру;

• рассчитать оптимальное число кластеров

4. Опишите полученные кластеры в терминах предметной области, дайте каждому кластеру условное наименование с учетом значимости признаков, повлиявших на выделение кластеров.

5. Сделать выводы по работе

Вариант 3. Датасет cancer.

В качестве среды разработки был выбран блокнот Colab — это бесплатная интерактивная облачная среда для работы с кодом на языке Python от Google в браузере: https://colab.research.google.com/.

Часть 1.

Для начала загрузим необходимые библиотеки.

Листинг 1.

import numpy as np

import pandas as pd

import matplotlib.pyplot as plt

import seaborn as sns

from mpl_toolkits import mplot3d

from sklearn.preprocessing import StandardScaler

from sklearn.cluster import KMeans

from sklearn.metrics import silhouette_score

from sklearn.metrics import davies_bouldin_score

from sklearn.cluster import AgglomerativeClustering

from scipy.cluster.hierarchy import dendrogram, linkage

from sklearn.metrics import silhouette_score, adjusted_rand_score, adjusted_mutual_info_score, fowlkes_mallows_score, homogeneity_score, completeness_score, v_measure_score

Функция make_data() принимала два аргумента: n (количество точек в каждом кластере) и seed (зерно для генерации случайных чисел). Она создавала данные, представляющие три кластера с нормальным распределением и добавила некоторый шум. Затем данные перемешивались, и результат представлялся в виде DataFrame с двумя столбцами 'x' и 'y'.

Используем функцию для создания набора данных.

Листинг 2.

def make_data(n, seed):

    np.random.seed(seed)

    shift_matrix = np.array([[3, 3], [6, 9], [9, 3]])

    data = np.random.randn(3, 2, n) + shift_matrix.reshape((3, 2, 1))

    data = np.swapaxes(data, 1, 2)

    data = data.reshape((-1, 2))

    data *= np.array([[20, 0.5]])

    df = pd.DataFrame({'x': data[:, 0], 'y': data[:, 1]}, columns=['x', 'y'])

    df = df.sample(frac=1.0)

    return df

Объект класса StandartScaler() был создан для стандартизации данных. Были сформированы два набора данных - обучающий и валидационный. Эти наборы были получены из вышеуказанной функции.

Для избежания неправильной стандартизации при использовании fit_transform на тестовом наборе было решено, что статистика (например, среднее и стандартное отклонение) из тестового набора не должна использоваться при обучении. Вместо этого, был использован метод fit_transform только на обучающем наборе. Затем к тестовому набору был применен метод transform, чтобы использовать те же параметры стандартизации, которые были выучены из обучающего набора (Рис. 1-2).

Листинг 3.

train_set = make_data(50, 11)

train_set

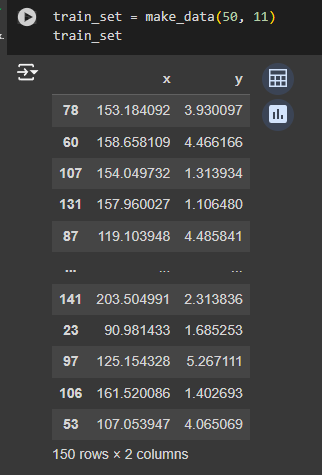
Рисунок 1 - Обучающий набор данных

Листинг 4.

sc = StandardScaler()

features = ['x', 'y']

train_set = make_data(50, 11)

test_set = make_data(50, 34)

train_set[features] = sc.fit_transform(train_set[features])

test_set[features] = sc.transform(test_set[features])

train_set

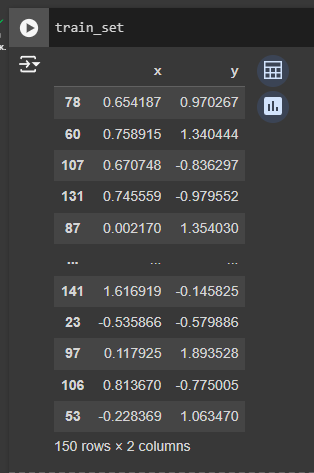
Рисунок 2 - Стандартизированный обучающий набор данных

Предоставленный код выполняет кластеризацию методом k-средних и визуализацию результатов на обучающем наборе данных. Сначала создается объект KMeans с указанием требуемого количества кластеров (в данном случае, 3) и фиксированным начальным состоянием для обеспечения воспроизводимости результатов.

Затем модель KMeans обучается на числовых признаках 'x' и 'y' обучающего набора данных с использованием метода fit_predict, который возвращает метки кластеров для каждого объекта. Полученные метки кластеров используются для создания массива, где столбцы 'x' и 'y' объединяются с соответствующими метками кластеров.

Для визуализации результатов используется scatter plot, где каждый объект обозначается цветом в зависимости от принадлежности кластеру. Также на графике отмечаются центры кластеров, обозначенные синими маркерами "o". Заголовок графика и легенда добавляются для более наглядного представления результатов (Рис. 3).

Листинг 5.

kmeans = KMeans(n_clusters = 3, random_state = 0, n_init=10)

train_labels = kmeans.fit_predict(train_set[features])

X_labeled = np.column_stack((train_set['x'], train_labels))

sns.scatterplot(x='x', y='y', hue=train_labels, data=train_set, palette='viridis', s=150, edgecolor='k', legend='full')

centers = kmeans.cluster_centers_

plt.scatter(centers[:, 0], centers[:, 1], c='blue', marker='o', s=300, label='Centers')

plt.title("Визуализация кластеров и центров")

plt.legend()

plt.show()

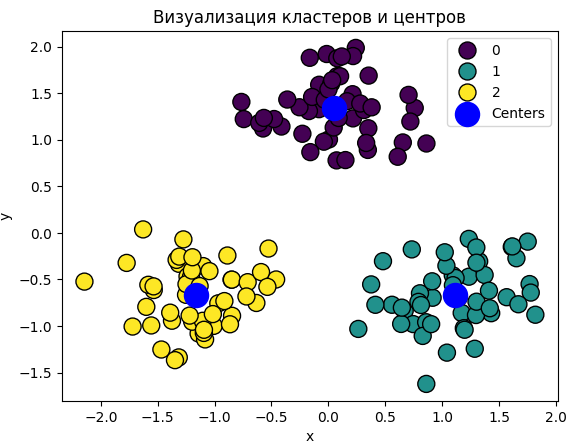
Рисунок 3 - Визуализация результатов

Полученная диаграмма показала, как были распределены кластеры. Каждый кластер обозначался своим цветом.

Модель, которая была получена вследствие обучения набором данных, имела высокую точность распределения на кластеры. Полученные наборы распределялись на три явно сконцентрированные в разных частях диаграммы группы. Центры кластеров также были визуально правильно отмечены.

Было выполнено предсказание меток кластеров для данных тестового набора с использованием предварительно обученной модели KMeans. После применения метода predict к числовым признакам 'x' и 'y' тестового набора, предсказанные метки кластеров были сохранены в переменной test_labels_predicted. Затем результаты были визуализированы на scatter plot, где каждый объект тестового набора был обозначен цветом в соответствии с предсказанным кластером.

На графике были также отмечены точки, представляющие центры кластеров, которые были предварительно вычислены на обучающем наборе данных. Для более ясного понимания содержания графика была добавлена легенда, обозначающая центры кластеров, а также указан заголовок графика (Рис. 4).

Листинг 6.

test_labels_predicted = kmeans.predict(test_set[features])

sns.scatterplot(x='x', y='y', hue=test_labels_predicted, data=test_set, palette='viridis', s=150, edgecolor='k', legend='full')

plt.scatter(centers[:, 0], centers[:, 1], c='blue', marker='o', s=300, label='Centers')

plt.legend()

plt.title("Предсказания кластеров и центры кластеров")

plt.show()

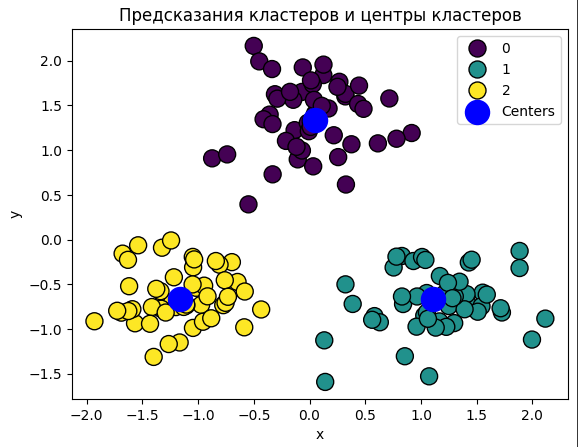
Рисунок 4 - Предсказания кластеров и центров

Предсказанные значения были точно распределены на ранее полученные кластеры. Полученная модель довольно точно могла определять принадлежность к определенному кластеру. Центры кластеров также были отмечены в местах, очень близких к предыдущим.

Коэффициент силуэта (Silhouette Score) - это метрика, используемая для оценки качества кластеризации данных. Он предоставляет меру того, насколько объект хорошо соответствует своему собственному кластеру по сравнению с другими кластерами. Значение коэффициента силуэта находится в диапазоне от -1 до 1.

Основные характеристики коэффициента силуэта:

• Значение близкое к 1 указывает на хорошую кластеризацию, где объекты внутри кластеров компактны и хорошо отделены от других кластеров.

• Значение близкое к 0 указывает на перекрывание кластеров или на точки, находящиеся на границе между кластерами.

• Отрицательные значения обычно указывают на неправильную кластеризацию.

Вычисление коэффициента силуэта обычно выполняется для каждого объекта по отношению к другим объектам в том же кластере и объектам в ближайшем соседнем кластере (Рис. 5).

Листинг 7.

silhouette_coefficient = silhouette_score(test_set[features], test_labels_predicted)

print("Коэффициент силуэта для данных test:", silhouette_coefficient)

Рисунок 5 - Коэффициент силуэта

Значение 0.70 указывает на хорошую кластеризацию, что доказывалось построением диаграммы - объекты внутри кластеров хорошо отделены, но не слишком компактны.

Функция cluster_creation() принимает два параметра: n, представляющий количество кластеров, и seed, который используется для инициализации генератора случайных чисел для воспроизводимости результатов. Данный программный код полностью повторял вышеприведенные блоки. Данная функция была создана для упрощения работы с различными количествами кластеров.

Листинг 8.

def cluster_creation(n, seed):

  kmeans = KMeans(n_clusters = n, random_state = seed, n_init=10)

  train_labels = kmeans.fit_predict(train_set[features])

  X_labeled = np.column_stack((train_set['x'], train_labels))

  sns.scatterplot(x='x', y='y', hue=train_labels, data=train_set, palette='viridis', s=150, edgecolor='k', legend='full')

  centers = kmeans.cluster_centers_

  plt.scatter(centers[:, 0], centers[:, 1], c='blue', marker='o', s=300, label='Centers')

  plt.title("Визуализация кластеров и центров")

  plt.legend()

  plt.show()

  test_labels_predicted = kmeans.predict(test_set[features])

  sns.scatterplot(x='x', y='y', hue=test_labels_predicted, data=test_set, palette='viridis', s=150, edgecolor='k', legend='full')

  plt.scatter(centers[:, 0], centers[:, 1], c='blue', marker='o', s=300, label='Centers')

  plt.legend()

  plt.title("Предсказания кластеров и центры кластеров")

  plt.show()

  silhouette_coefficient = silhouette_score(test_set[features], test_labels_predicted)

  print("Коэффициент силуэта для данных test:", silhouette_coefficient)

Тот же набор данных был разделен на два кластера с визуализацией с помощью вышеуказанной функции (Рис. 6-7).

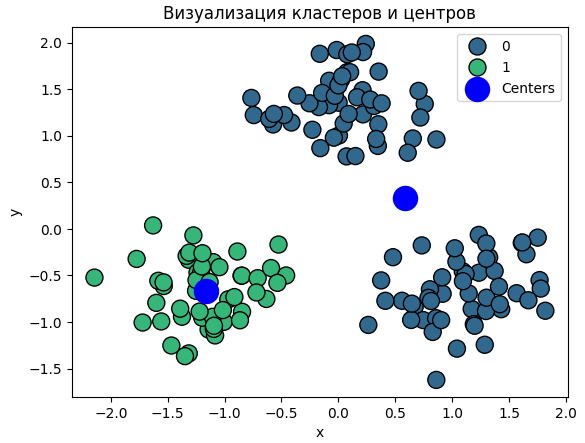
Рисунок 6 - Визуализация кластеров и центров

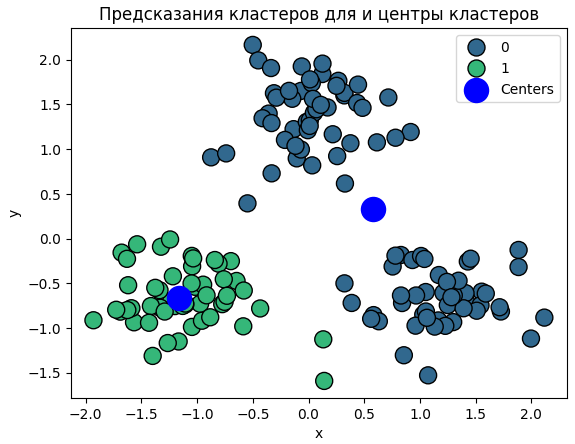
Рисунок 7 - Предсказания кластеров и центров

Данные были логично разделены на два кластера. Однако после визуализации данных было замечено неуместность применения двух кластеров. Кластер зеленого цвета был похож на кластер из предыдущей части, но второй кластер (синего цвета) имел центр там, где не было ни одной точки. Следовательно, второй кластер можно было разделить на два, как это было сделано раньше.

Далее было выделено четыре кластера (Рис. 8-9).

Рисунок 8 - Визуализация кластеров и центров

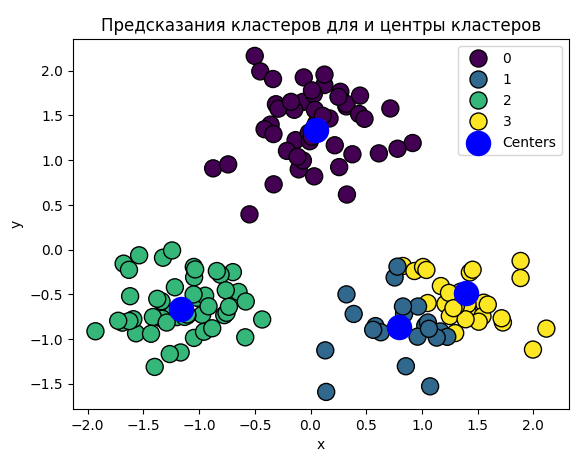
Рисунок 9 - Предсказания кластеров и центров

Деление на четыре кластера было рассмотрено как излишнее, особенно визуально, где синий и желтый кластеры могли быть объединены. Это деление казалось необязательным.

Для подтверждения гипотезы о том, что деление на три кластера было наиболее рациональным и достаточным, использовался метод локтя.

Метод локтя использовался для определения оптимального количества кластеров в модели. График зависимости суммы квадратов расстояний от каждой точки до центроида своего кластера строился в зависимости от количества кластеров (Рис. 10).

Листинг 9.

data_for_elbow = train_set[features]

inertia = []

k_values = list(range(1, 11))

for k in k_values:

    kmeans = KMeans(n_clusters=k, random_state=0, n_init=10)

    kmeans.fit(data_for_elbow)

    inertia.append(np.sqrt(kmeans.inertia_))

plt.plot(k_values, inertia, marker='o')

plt.title('Метод локтя')

plt.xlabel('Количество кластеров')

plt.ylabel('Сумма квадратов расстояний')

plt.show()

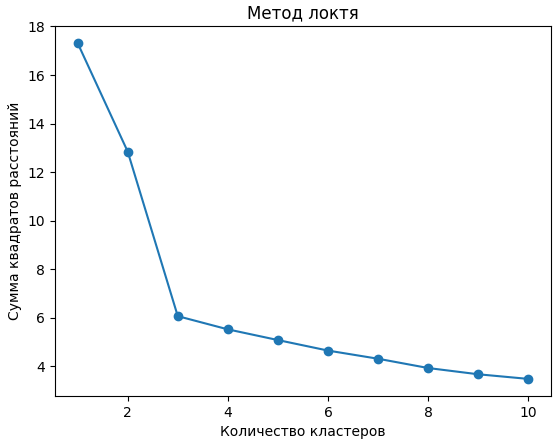
Рисунок 10 - Метод локтя

На графике можно было заметить точку, где увеличение числа кластеров перестает существенно уменьшать сумму квадратов расстояний, и этот момент считается оптимальным числом кластеров (похож на локоть). На данном примере "перелом" происходил в значении три, следовательно, гипотеза о трех кластерах оказалось верной.

Часть 2.

Вариант 3, данные содержат информацию показателях в крови пациентов:

Id – содержит идентификатор пациента, число не отрицательное.

Clump_thickness – содержит толщину скопления, число.

Size_uniformity – содержит однородность скопления клеток, число.

Shape_uniformity – содержит однородность формы клеток, число.

Marginal_adhesion – указывает на краевую адгезию, число.

Epithelial_size – содержит размер отдельных эпителиальных клеток, число.

Bare_nucleoli – указывает на голые ядра, число.

Bland_chromatin – указывает на белый хроматин, число.

Normal_nucleoli – содержит нормальные ядрышки, число.

Mitoses – содержит метозы, число.

Class – класс, содержит значения '2' – доброкачественные, '4' - злокачественные.

Первым делом загружаются необходимые библиотеки для лабораторной работы.

Листинг 10.

import pandas as pd

import csv

import matplotlib.pyplot as plt

import numpy as np

from sklearn.preprocessing import StandardScaler

from sklearn.cluster import KMeans

from scipy.cluster.hierarchy import dendrogram, linkage

from sklearn.metrics import silhouette_score

from scipy.spatial import distance

from sklearn.cluster import AgglomerativeClustering

from yellowbrick.cluster import KElbowVisualizer

import seaborn as sns

Специально для Google Colab загрузим необходимый файл csv (Рис. 11).

Рисунок 11 - Загрузка файла

На экран выводятся первые 10 строк из файла (Рис. 12).

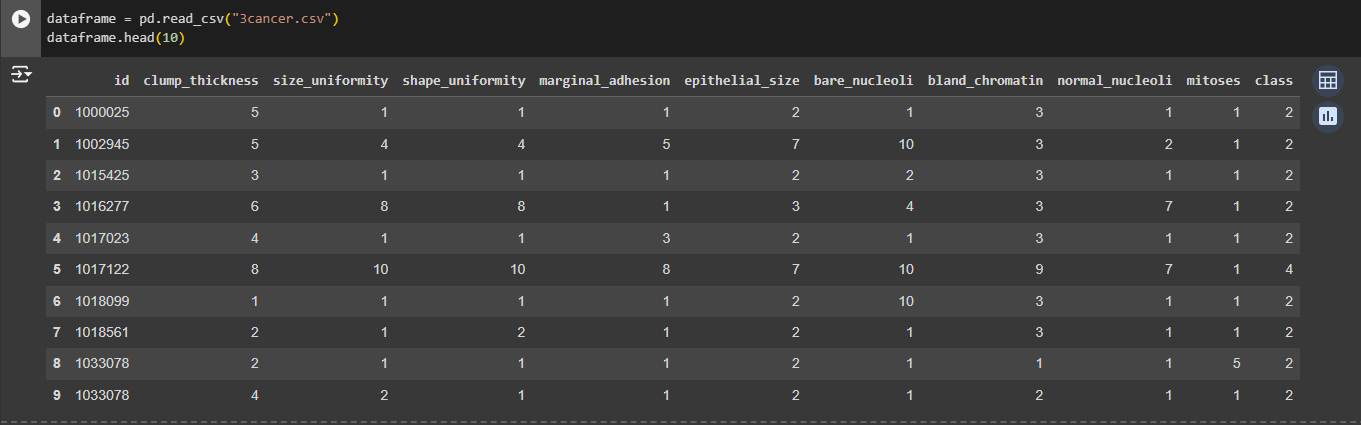
Рисунок 12 - Вывод строк

Далее необходимо оценить данные. Видно, что столбец "bare_nucleoli" имеет неверный тип данных (Рис. 13).

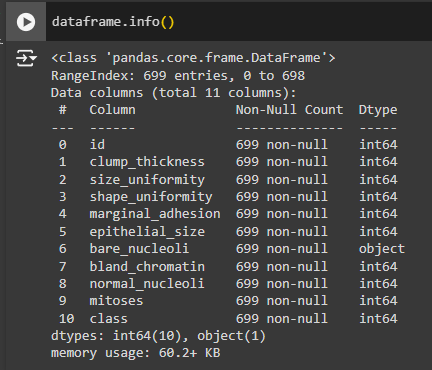
Рисунок 13 - Оценка данных

По оценке данных мы можем заметить, что данных с пустыми значениями нет. Получается, что пропусков в данных нет. С помощью метода df.isna().sum() видно, что в сумме 0 пропусков, от которых нужно избавляться не нужно (Рис. 14).

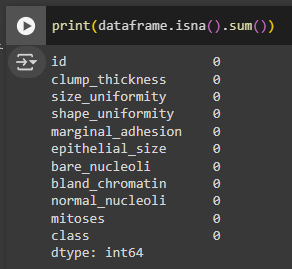
Рисунок 14 - Поиск пропусков

Явные дубликаты рациональнее удалять уже после устранения неявных, а именно замены, объектов, имеющих немного отличающиеся названия, но при этом являющихся одним и тем же объектом по сути (Рис. 15).

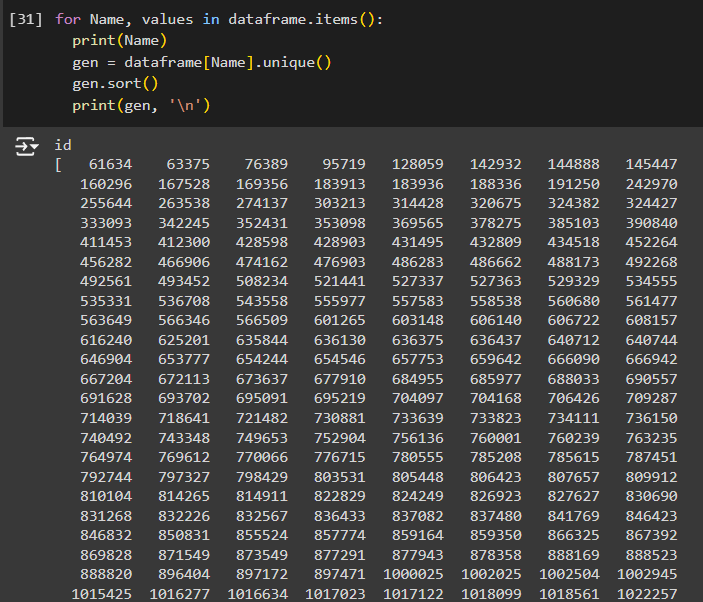
Рисунок 15 - Поиск дубликатов

Было обнаружено некорректное значение, а именно в колонке «bare_nucleoli» - «?».

Неправильное написание значения было исправлено методом replace(). В первом аргументе ему передают нежелательное значение из таблицы. Во втором - новое значение, которое должно заменить дубликат (Рис. 16).

Листинг 12.

dataframe['bare_nucleoli'] = dataframe['bare_nucleoli'].replace('?', '2')

for Name in ['bare_nucleoli']:

  print(Name)

  gen = dataframe[Name].unique()

  gen.sort()

  print(gen, '\n')

Рисунок 16 - Замена некорректного поля

Производится проверка на наличие явных дубликатов, и таковых обнаружено 8 штук (Рис. 17).

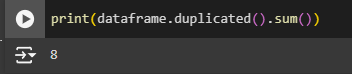
Рисунок 17 - Поиск явных дубликатов

Чтобы избавиться от таких дубликатов используется метод drop_duplicates().

После удаления строчек обновляем индексацию: чтобы в ней не осталось пропусков. Для этого применяется метод reset_index(). Он создаст новый датафрейм, где:

индексы исходного датафрейма станут новой колонкой с названием index;

все строки получат обычные индексы, уже без пропусков (Рис. 18).

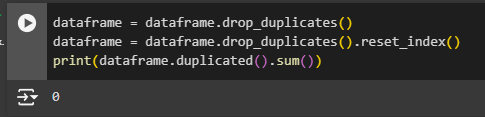
Рисунок 18 - Удаление явных дубликатов

С помощью метода df.dtypes производится проверка типов данных столбцов (Рис. 19).

Рисунок 19 - Проверка типов данных столбцов

Необходимо поменять тип данных столбца " bare_nucleoli " на целочисленный, а после ещё раз проверить правильность (Рис. 20).

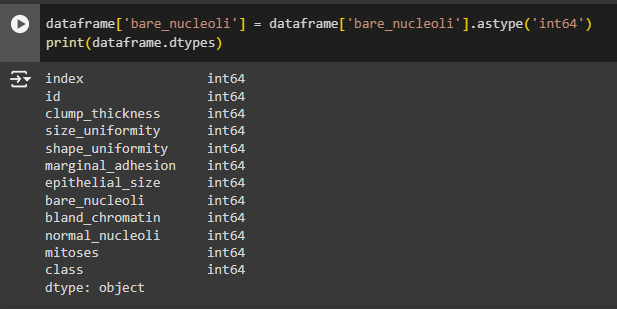
Рисунок 20 - Изменение типа данных столбца

Для кластеризации необходимо убрать целевой столбец Class и столбцы index и id (Рис. 21).

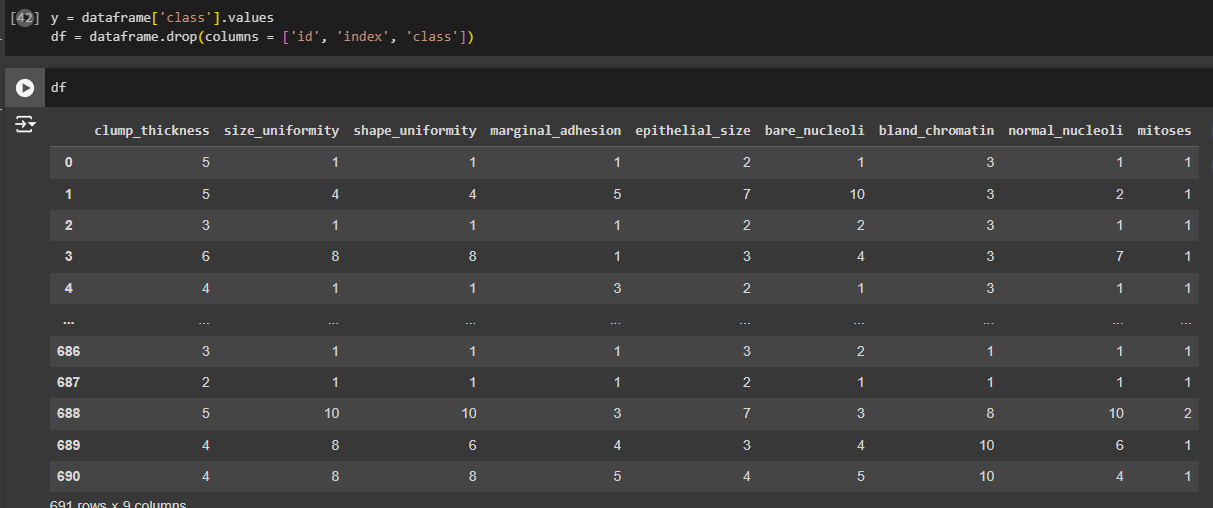
Рисунок 21 - Удаление столбцов из датафрейма

Создаётся объект класса scaler, далее он обучается по текущему набору данных, а после данные стандартизируются (Рис. 22).

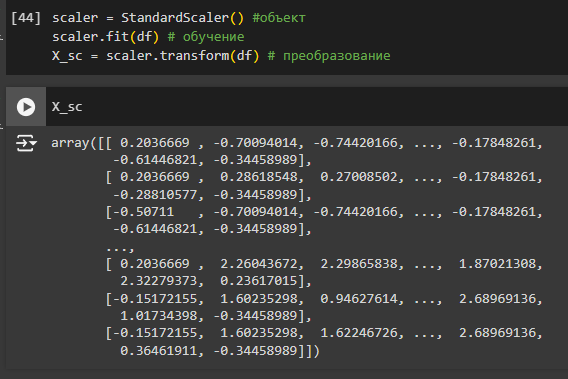
Рисунок 22 – Обучение

По этим данным строится дендрограмма (Рис. 23).

Листинг 13.

linked = linkage(X_sc, method = 'ward')

plt.figure(figsize=(15, 10))

dendrogram(linked, orientation='top', truncate_mode = "lastp")

plt.title('Иерархическая кластеризация показателей в крови пациентов')

plt.show()

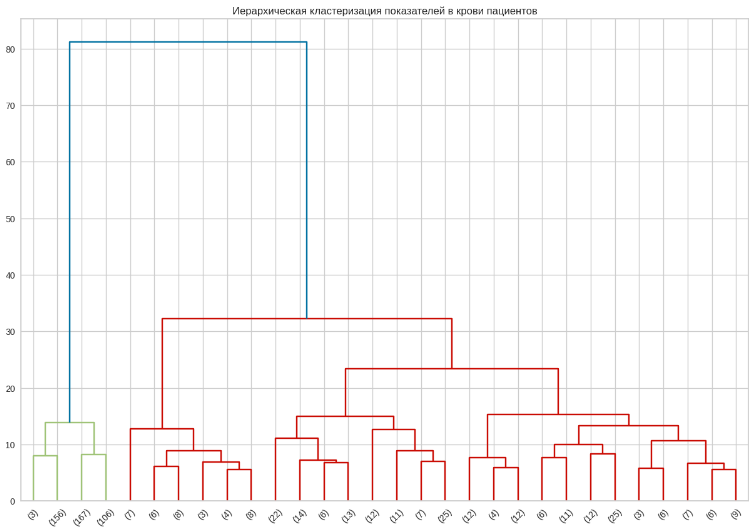
Рисунок 23 - Дендрограмма

Оптимальное число кластеров, судя по дендрограмме - 2. Некоторые значения встречаются в разных кластерах (12). Из этого следует, что текущие данные невозможно распределить по однозначно определённым кластерам, а, значит, могут быть получены неверные результаты.

Для выбора оптимального количества кластеров воспользуемся методом локтя (Рис. 24).

Листинг 14.

model = AgglomerativeClustering()

visualizer = KElbowVisualizer(model, k=(1,11), timings=False)

visualizer.fit(df)

visualizer.show()

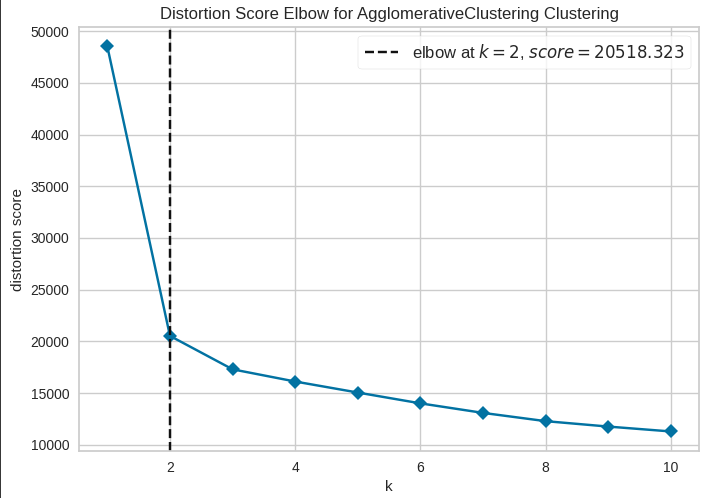
Рисунок 24 - Метод локтя

Метод локтя показал, что оптимальным числом кластеров является 2.

Проверяется, для какого количества кластеров кластеризация будет наиболее качественной.

Задаётся количество кластеров, равное 2, а далее изучается набор данных (Рис. 25).

Листинг 15.

km = KMeans(n_clusters=2,random_state=0)  #задаем количество кластеров

km.fit(X_sc)

label = km.fit_predict(X_sc)

silhouette_score(X_sc, label)

Рисунок 25 - Метрика силуэта для 2 кластеров

Повторим для количества кластеров 3 и 4 (Рис. 26-27).

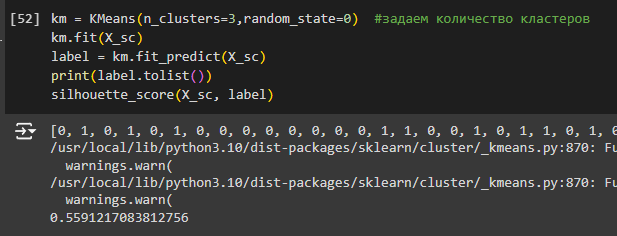
Рисунок 26 - Метрика силуэта для 3 кластеров

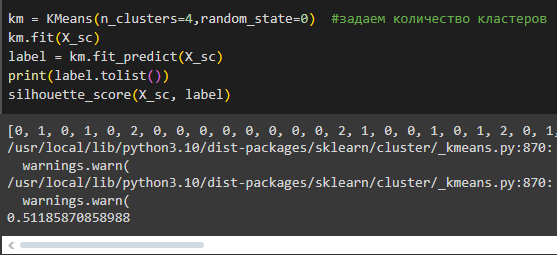
Рисунок 27 - Метрика силуэта для 4 кластеров

По метрикам видно, что кластеризация ни в одном из случаев не может быть проведена качественно, однако деление на 2 кластера показало лучший результат. Именно такое количество кластеров будет задаваться для метода k-средних.

Выводятся центроиды кластеров (Рис. 28).

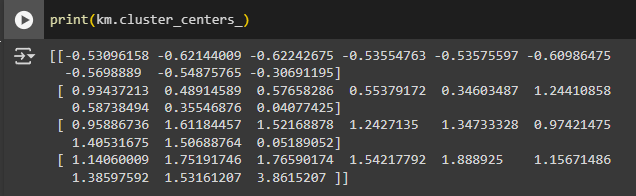
Рисунок 15 - Центроиды кластеров

Вычисляется Евклидово расстояние между кластерами, и оно записывается в матрицу, где элемент aij матрицы - Евклидово расстояние между кластерами i и j соответственно (Рис. 29).

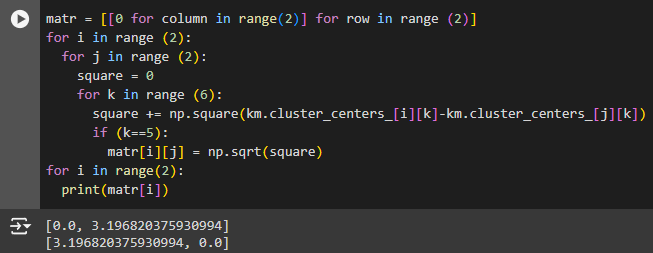
Рисунок 29 - Матрица Евклидовых расстояний

В набор данных добавляется ещё один столбец - cluster, который показывает, к какому из двух кластеров принадлежит данная строка. Также выводятся первые 10 строк набора данных, чтобы убедиться, что этот столбец добавлен (Рис. 30).

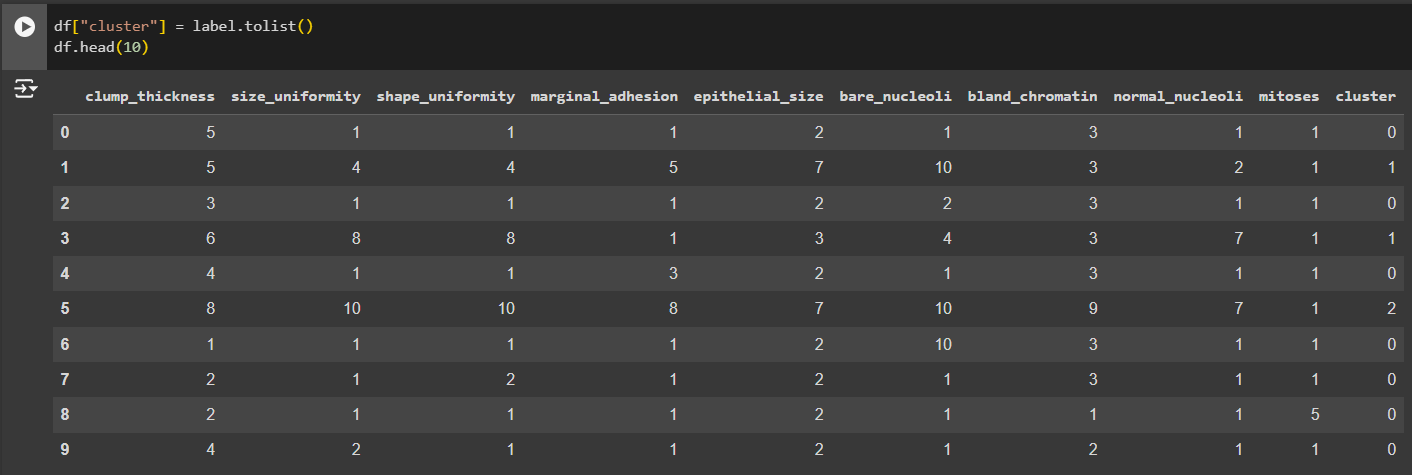
Рисунок 16 - Добавление поля cluster

С помощью метода describe() просматриваются средние значения по каждому из столбцов, а также их средние отклонения (Рис. 31).

Рисунок 17 - Анализ полей

Строится график деления пациентов по столбцу "class" (Рис. 32).

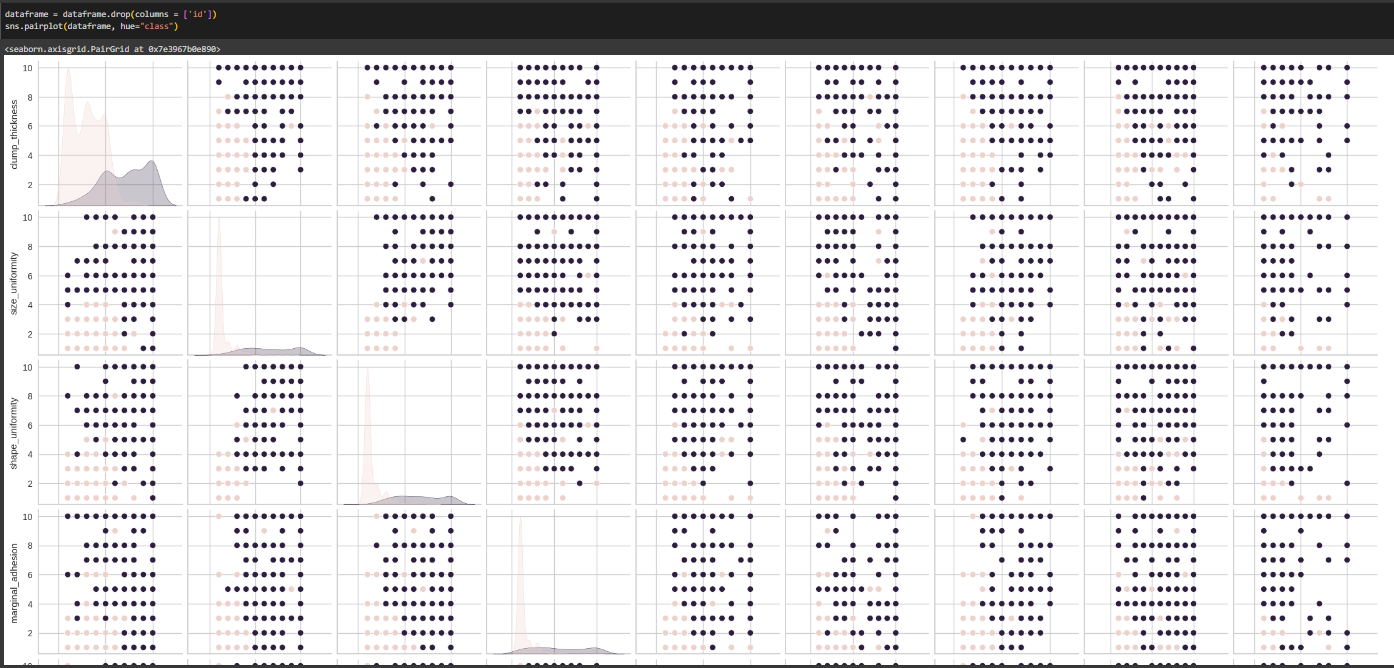
Рисунок 18 - График деления пациентов по столбцу class

Исходя из графика, нельзя точно определить, какие именно признаки оказывают наибольшее влияние на целевой признак. Однако можно отследить, какие параметры коррелируют с ним, исходя из количества розовых точек на графиках.

Вывод

В ходе выполнения лабораторной работы были изучены алгоритмы и методы кластерного анализа на практике.

Данные представляли собой набор сведений о показателях в крови пациентов свидетельствующие о предрасположенности к заболеванию.

Была осуществлена предварительная обработка данных csv-файла, а именно: были осуществлены проверки на наличие пропусков и дубликатов, а также их удаление. Был изменен неправильный тип данных определенного столбца.

После этого данные были стандартизированы и разделены на кластеры двумя методами: иерархическим агломеративным методом и методом k-средних. Были выявлены признаки, которые оказали наибольшее влияние на выделение кластеров. Исходя из дендрограммы разделения на кластеры, оптимальным количеством кластеров является 2, что также показала метрика силуэта. При таком количестве кластеров метрика составляет около 57%. Метод локтя при этом показал оптимальное деление на 2 кластера, что подтверждается метрикой силуэта.

В результате работы можно прийти к выводу, что кластеризация может быть полезным инструментом для анализа данных и выделения групп объектов с похожими характеристиками. Однако необходимо тщательно подбирать параметры алгоритмов кластеризации и проводить предварительную обработку данных для достижения наилучших результатов.

Посмотреть на реализацию лабораторной работы в Colab можно по следующей ссылке:

https://colab.research.google.com/drive/1S3j0_S94lq38KjxCqUkxNUSo5-Gzfd1H#scrollTo=LkJdZB5Rr5wJ