
ио
.docxМИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное автономное образовательное учреждение высшего образования
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»
Кафедра 41
ПРЕПОДАВАТЕЛЬ
Ст. преподаватель |
|
|
|
Н. Н. Григорьева |
должность, уч. степень, звание |
|
подпись, дата |
|
инициалы, фамилия |
Контрольная работа
по курсу: Исследование операций
СТУДЕНТКА ГР. № |
Z0411 |
|
31.05.24 |
|
М. В. Карелина |
|
|
номер группы |
|
подпись, дата |
|
инициалы, фамилия |
|
Номер студенческого билета: 2020/3477
Санкт-Петербург
2024
Задание 1. Линейное программирование. Графическая интерпретация и симплекс-метод.
Вариант 8.

Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (Рис. 1).
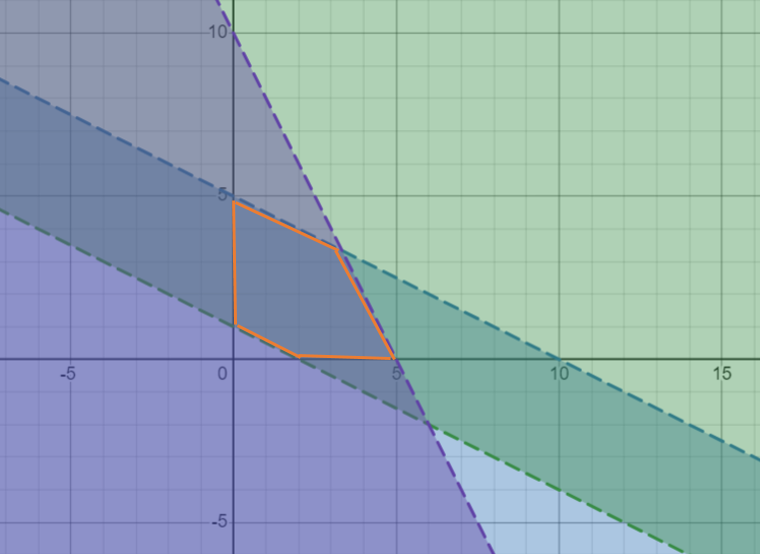
Рисунок 1 - Границы области допустимых решений.
Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи (область в красных линиях).
Рассмотрим целевую функцию задачи F = 4x1+3x2 -> max. Построим прямую, отвечающую значению функции F = 4x1+3x2 = 0 (Рис. 2).
Будем
двигать эту прямую параллельным образом.
Поскольку нас интересует максимальное
решение, поэтому прямая будет двигаться
вверх до
касания фиолетовой линии 4x1+3x2 =>23.333333. (Рис. 3).
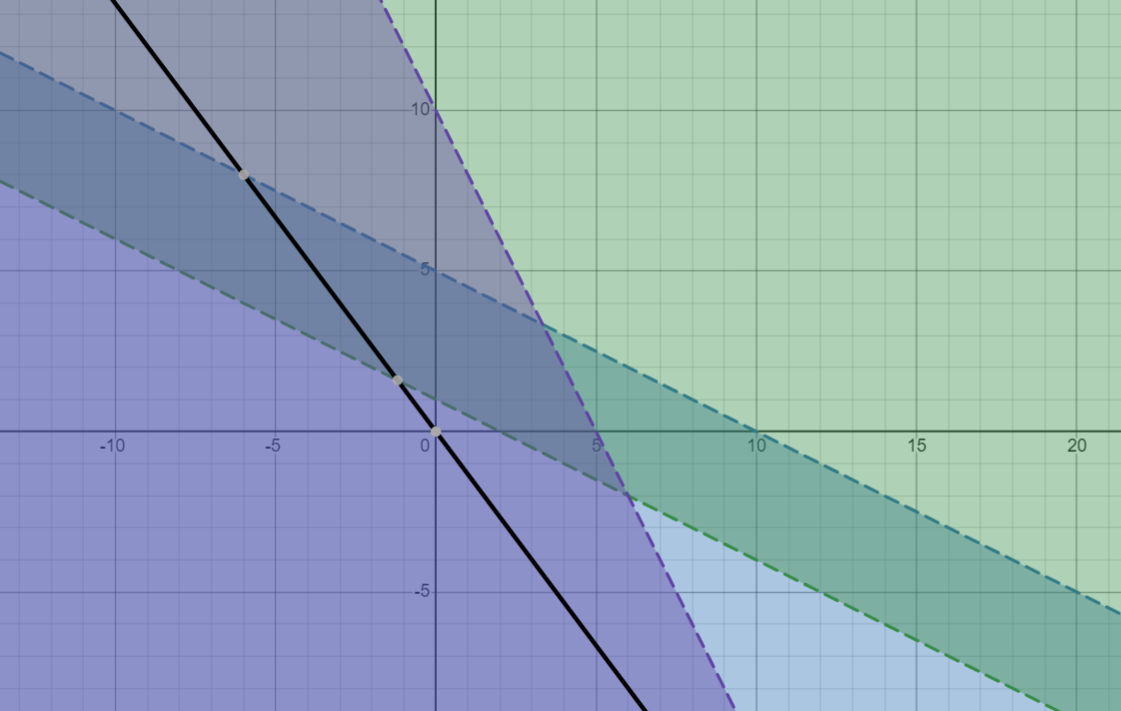
Рисунок 2 - Целевая функция

Рисунок 3 - Определение оптимального решения задачи
Соответственно, максимальное значение целевой функции 4x1+3x2 =>23.333333.
Проверим это в программе MS Excel (Рис. 4).

Рисунок 4 - Проверка в программе Excel
Решение задачи Симплекс-методом
 В
1-м неравенстве смысла (≤) вводим базисную
переменную y1. В 2-м неравенстве смысла
(≥) вводим базисную переменную y2 со
знаком минус. В 3-м неравенстве смысла
(≤) вводим базисную переменную y3.
В
1-м неравенстве смысла (≤) вводим базисную
переменную y1. В 2-м неравенстве смысла
(≥) вводим базисную переменную y2 со
знаком минус. В 3-м неравенстве смысла
(≤) вводим базисную переменную y3.
 +2
+2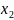 +
+ =10
=10
+2
-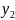 =2
=2
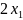 +
+
+
+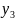 =10
=10
=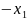 −2
+10
−2
+10
=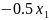 +0.5
+1
+0.5
+1
=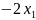 −
+10
−
+10
=8−
= +0.5 +1
=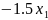 −
−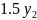 +9
+9
L=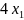 +1.5
+1.5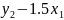 +3=3+1.5
+3=3+1.5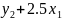
=8−
=
−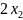 +2
+2
=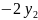 +3
+6
+3
+6
L=8+4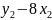 +3
=8+4
+3
=8+4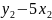
=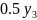 −1.5
+5
−1.5
+5
=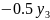 −
−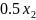 +5
+5
=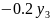 +
+3
+
+3
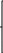
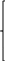 L=
L=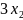 −2
−2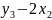 +20=−2
+20=−2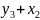 +20
+20
=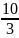 +
+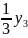 −
−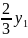
=
−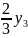 −
−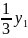
=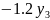 −0.5
+8
−0.5
+8
L=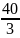 −
−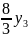 −
−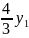 +
+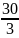 +
-2
=
+
-2
=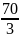 −
−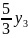 −
−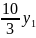
Lmax= =23.333
Проверка Симплекс-методом и Excel дала один результат.
Задание 2.
Вариант 8.
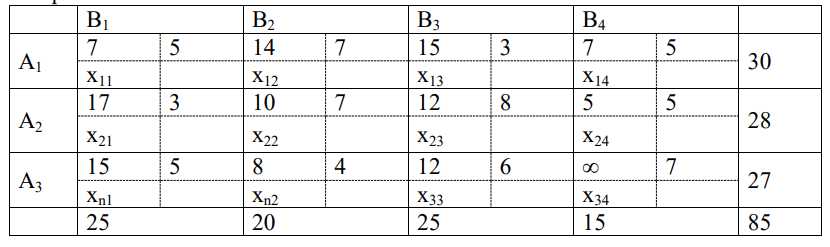
В данной задаче нам нужно определить оптимальный план перевозок ТЗ с ограничениями в сетевой форме.
Используя метод северо-западного угла, построим первый опорный план транспортной задачи.
Работа алгоритма начинается с клетки (1,1). Сравниваем a1 и b1, выбираем из них минимальное значение. Записываем это значение в поле x11; таким образом, полностью удовлетворена заявка первого потребителя, а запас первого склада необходимо скорректировать. Далее заполняем ячейки советующим образом. (Рис. 5)
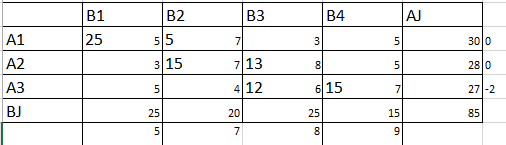
Рисунок 5 – оптимальный план перевозок ТЗ (Метод северо-западного угла)
Данный алгоритм очень простой и быстрый, но, поскольку мы игнорируем информацию о стоимости перевозок, вряд ли полученный план перевозок будет близок к оптимальному. В рассматриваемом примере стоимость плана составит:
Z1=25*5+5*7+15*7+13*8+12*6+15*7=125+35+105+104+72+105=546
Такая стоимость не удовлетворяет заказчика поэтому мы осуществляем перенос значений с помощью потенциалов. (Рис. 6)
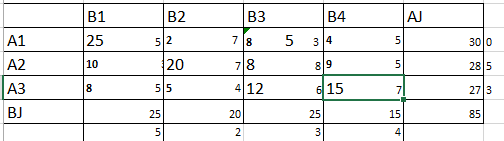
Рисунок 6 – оптимальный план перевозок ТЗ (Метод северо-западного угла)
Z2=25*5+5*3+20*7+8*8+12*6+15+7=125+15+140+64+72+105=521
Такая стоимость не удовлетворяет заказчика поэтому мы осуществляем перенос значений с помощью потенциалов. (Рис. 7)
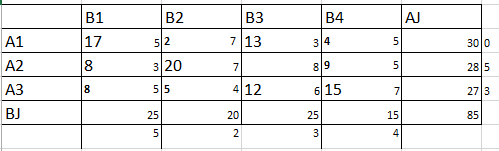
Рисунок 7 – оптимальный план перевозок ТЗ (Метод северо-западного угла)
Z3=17*5+13*3+8*5+20*7+12*6+15*7=85+39+40+140+72+105=481
Такая стоимость не удовлетворяет заказчика поэтому мы осуществляем перенос значений с помощью потенциалов. (Рис. 8)
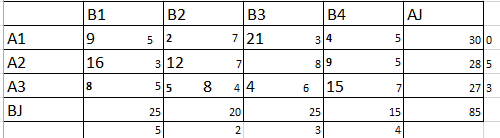
Рисунок 8 – оптимальный план перевозок ТЗ (Метод северо-западного угла)
Z4=9*5+21*3+16*3+12*7+8*4+4*6+15*7=45+63+48+84+32+24+105=401
Такая стоимость не удовлетворяет заказчика поэтому мы осуществляем перенос значений с помощью потенциалов. (Рис. 9)
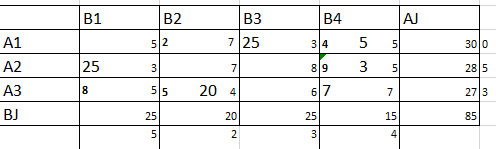
Рисунок 9 – оптимальный план перевозок ТЗ (Метод северо-западного угла)
Z5=25*3+5*5+25*3+3*5+20*4+7*7=75+25+75+15+80+49=319
В итоге мы пришли к удовлетворяющему значению.
Далее используется метод минимальной стоимости. Как следует из его названия, на каждом шаге алгоритма для заполнения выбирается клетка с минимальной стоимостью перевозки.
Рассмотрим работу алгоритма на том же примере. (Рис. 10)
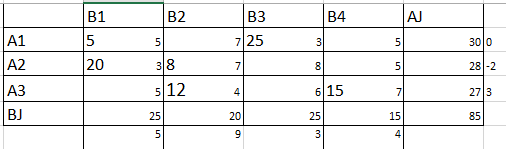
Рисунок 10 – оптимальный план перевозок ТЗ (Метод минимальной стоимости)
Z6=5*5+20*3+8*7+12*4+25*3+15*7=25+60+56+48+75+105=369
Такая стоимость не удовлетворяет заказчика поэтому мы осуществляем перенос значений с помощью потенциалов. (Рис. 11)
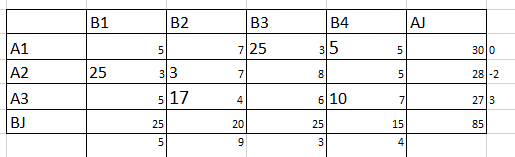
Рисунок 11 – оптимальный план перевозок ТЗ (Метод минимальной стоимости)
Z7=25*3+5*5+25*3+3*7+17*4+10*7=75+25+75+21+70+68=334
Такая стоимость не удовлетворяет заказчика поэтому мы осуществляем перенос значений с помощью потенциалов. (Рис. 12)
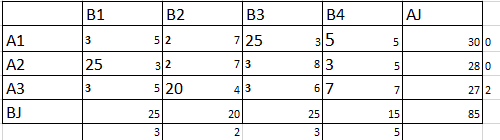
Рисунок 12 – оптимальный план перевозок ТЗ (Метод минимальной стоимости)
Z8=25*3+5*5+25*3+3*5+20*4+7*7=75+25+75+15+80+49=319
В итоге мы пришли к удовлетворяющему значению гораздо быстрее используя этот метод.
Оптимизируем опорный план ТЗ с ограничениями, методом северо-западного угла с использованием потенциалов. (Рис. 13)
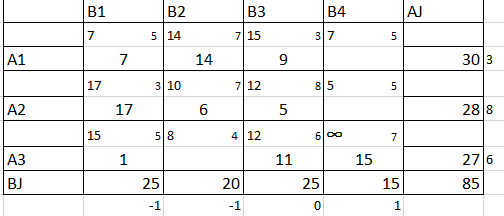
Рисунок 13 – оптимальный план перевозок ТЗ (Метод северо-западного угла)
Z9=7*5+14*7+9*3+17*3+6*7+5*8+1*5+11*6+15*7=35+98+27+51+42+40+5+66+105=469
Такая стоимость не удовлетворяет заказчика поэтому мы осуществляем перенос значений с помощью потенциалов. (Рис. 14)
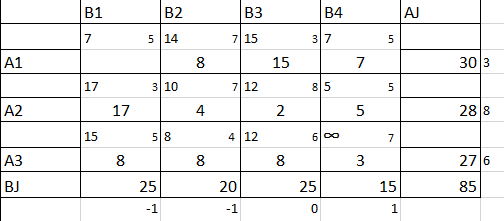
Рисунок 14 – оптимальный план перевозок ТЗ (Метод северо-западного угла)
Z10=8*7+15*3+7*5+17*3+4*7+2*8+5*5+8*5+8*4+8*6+3*7=56+45+35+51+28+16+25+40+32+48+21=397
Такая стоимость не удовлетворяет заказчика поэтому мы осуществляем перенос значений с помощью потенциалов. (Рис. 15)
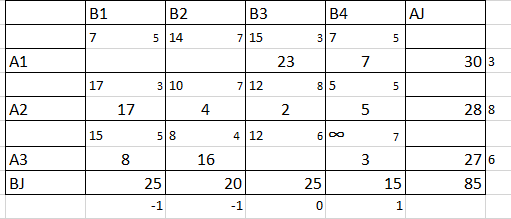
Рисунок 15 – оптимальный план перевозок ТЗ (Метод северо-западного угла)
Z11=23*3+7*5+17*3+4*7+2*6+5*5+8*5+16*4+3*7=69+35+51+28+12+25+40+64+21=342
В итоге мы пришли к удовлетворяющему значению. Оптимальный план (без ограничений + метод северо-западного угла) = 319, оптимальный план (без ограничений + метод мин.стоимости) = 319, оптимальный план (с ограничениями + метод северо-западного угла) = 342
Задание 3.
Решить задачу эвакуации при заданном ограничении на грузоподъемность G. Каждый из предметов – в единственном числе.
Вариант 8.

Процесс предварительной оптимизации будем фиксировать в таблице. (Рис. 16)
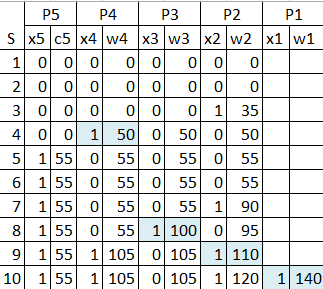
Рисунок 16 – процесс оптимизации
Ответ: x1 = 0, x2 = 1, x3 = 0, x4 = 1.
Ограничение по весу выполняется, суммарная стоимость предметов составляет 140 единиц.
Задача распределения ресурсов.
Будем рассматривать задачу распределения ресурсов на примере распределения ограниченной суммы ресурсов между несколькими предприятиями. При этом для каждого предприятия задана зависимость прибыли от суммы вложенных средств. За отдельный этап берется решение о выделении определенных ресурсов одному из предприятий. (Рис. 17)
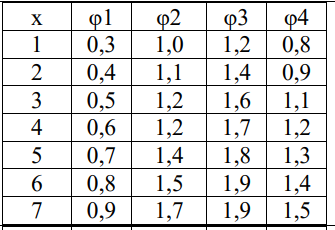
Рисунок 17 – Зависимость прибыли от суммы вложенных средств
При заполнении столбца, относящегося к последнему этапу, то есть к выделению средств четвертому предприятию, мы не берем в расчет последствий этого действия, то есть всю имеющуюся сумму выделяем третьему предприятию. Но для предварительной оптимизации остальных предприятий нам приходится проверять все варианты распределения средств и их последствия. Для этого так же, как и в предыдущем случае, делаются вспомогательные расчеты, примеры которых приведены на рисунках 18-20.
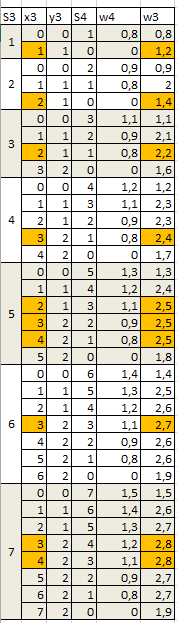
Рисунок 18 – Вспомогательные расчеты
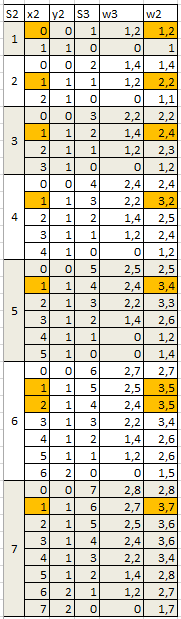
Рисунок 19 – Вспомогательные расчеты
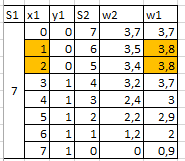
Рисунок 20 – Вспомогательные расчеты
Итоговый вид таблицы оптимизации. (Рис. 21)
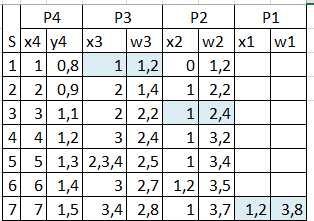
Рисунок 18 – Таблица оптимизации
Таким образом, мы видим, что есть четыре способа решения задачи распределения ресурсов:
1. x1=1, x2=2, x3=3, x4=1
2. x1=2, x2=1, x3=3, x4=1
3. x1=3, x2=1, x3=2, x4=1
4. x1=3, x2=2, x3=1, x4=1
Суммарный доход составит 3,8 единиц.
Задание 4.
Вариант 8.

Проверяем, имеет ли платежная матрица седловую точку. Если да, то выписываем решение игры в чистых стратегиях. Считаем, что игрок В выбирает свою стратегию так, чтобы получить максимальный свой выигрыш, а игрок А выбирает свою стратегию так, чтобы минимизировать выигрыш игрока В.
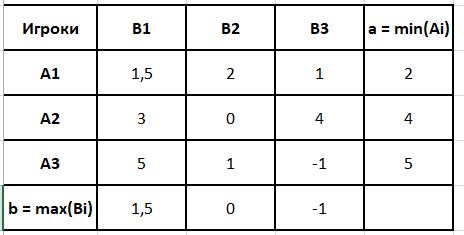
Находим гарантированный выигрыш, определяемый нижней ценой игры a = max(аi) = 5, которая указывает на максимальную чистую стратегию A3. Верхняя цена игры b = min(bj) = 1,5. Что свидетельствует об отсутствии седловой точки, так как a ≠ b. Решение игры в смешанных стратегиях. Объясняется это тем, что игроки не могут объявить противнику свои чистые стратегии: им следует скрывать свои действия. Игру можно решить, если позволить игрокам выбирать свои стратегии случайным образом (смешивать чистые стратегии).
Ответ: нижняя цена = 1,5, верхняя цена = 5, игра не имеет решение в чистых стратегиях.
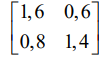
нижняя цена игры B = 0.6
верхняя цена игры A = 1.6
Находим решение игры в смешанных стратегиях. Запишем систему уравнений. Для игрока I 1.6p1+0.8p2 = y 0.6p1+1.4p2 = y p1+p2 = 1
Для игрока II 1.6q1+0.6q2 = y 0.8q1+1.4q2 = y q1+q2 = 1
Формулы:
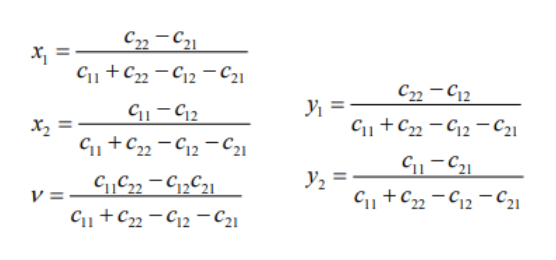
Решая эти системы, находим:
y = 1.1 p1 = 0.375 (вероятность применения 1-ой стратегии). p2 = 0.625 (вероятность применения 2-ой стратегии).
Оптимальная смешанная стратегия игрока I: P = (0.375; 0.625) q1 = 0.5 (вероятность применения 1-ой стратегии). q2 = 0.5 (вероятность применения 2-ой стратегии).
Оптимальная смешанная стратегия игрока II: Q = (0.5; 0.5) Цена игры: y = 1.1
Ответ: y=1.1 P(0.375, 0.625) Q(0.5, 0.5)
Теперь найдем решение той же игры по Нэшу, рассчитав математическое ожидание выигрыша А:
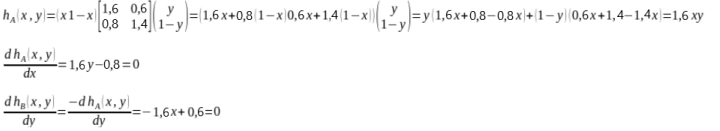
Отсюда получаем y = 0.5, x = 0.375. Соответственно, можем определить цену игры в точке равновесия по Нэшу:
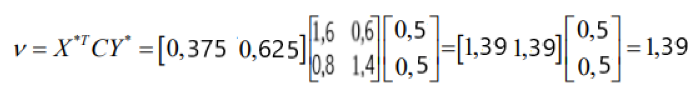
Как видно, результаты решения обоими способами совпали.
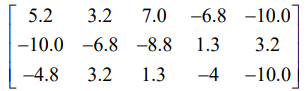
Такая матрица не удовлетворяет значениям поэтому добавим к каждому числу 11.
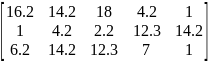
Провести сокращение размерности матрицы игры до формата m×2 или 2×n и найти ее решение в смешанных стратегиях графическим методом. Представить задачу в виде задачи линейного программирования и решить ее с помощью MS Excel.
Проверяем платежную матрицу на доминирующие строки и доминирующие столбцы.
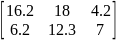
В платежной матрице отсутствуют доминирующие строки. Мы свели игру 5 x 3 к игре 2 x 3.
Так как игроки выбирают свои чистые стратегии случайным образом, то выигрыш игрока А будет случайная величина. В этом случае игрок А должен выбрать свои смешанные стратегии так, чтобы получить максимальный средний выигрыш.
Аналогично, игрок В должен выбрать свои смешанные стратегии так, чтобы минимизировать математическое ожидание игрока А.
Находим решение игры в смешанных стратегиях графическим методом.
Решим задачу геометрическим методом, который включает в себя следующие этапы: 1. В декартовой системе координат по оси абсцисс откладывается отрезок, длина которого равна 1. Левый конец отрезка (точка х = 0) соответствует стратегии A1, правый - стратегии A2 (x = 1). Промежуточные точки х соответствуют вероятностям некоторых смешанных стратегий S1 = (p1,p2). 2. На левой оси ординат откладываются выигрыши стратегии A1. На линии, параллельной оси ординат, из точки 1 откладываются выигрыши стратегии A2. Решение игры (2 x n) проводим с позиции игрока A, придерживающегося максиминной стратегии. Доминирующихся и дублирующих стратегий ни у одного из игроков нет. Выделяем нижнюю границу выигрыша B2NB3. Максиминной оптимальной стратегии игрока A соответствует точка N, лежащая на пересечении прямых B2B2 и B3B3, для которых можно записать следующую систему уравнений: y = 16,2 + (6,2 – 16,2)p2 y = 4,2 + (7 – 4,2)p2 Откуда p1 = 0.0625, p2 = 0.938. Цена игры, y = 6.825 Теперь можно найти минимаксную стратегию игрока B, записав соответствующую систему уравнений, исключив стратегию B2, которая дает явно больший выигрыш игроку B, и, следовательно, q1 = 0,218. q2 = 0,781 .
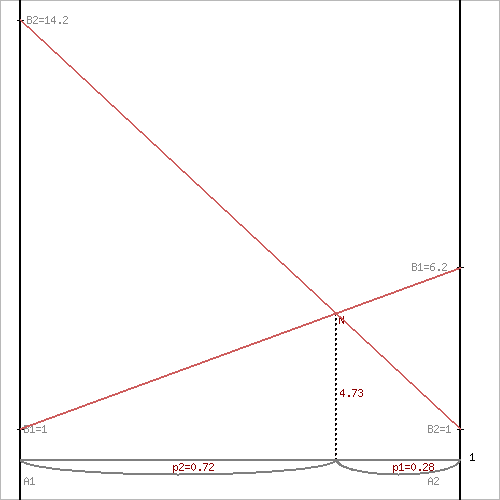
Рисунок 19 - Решение игры графическим методом
Ответ: Цена игры: y = 6,825, векторы стратегии игроков: Q(0,218, 0, 0,781), P(0,0625, 0,938)
Проверка в Excel:
С помощью дополнения «Поиск решения» удалось подтвердить корректность результатов. (Рис. 20-21)
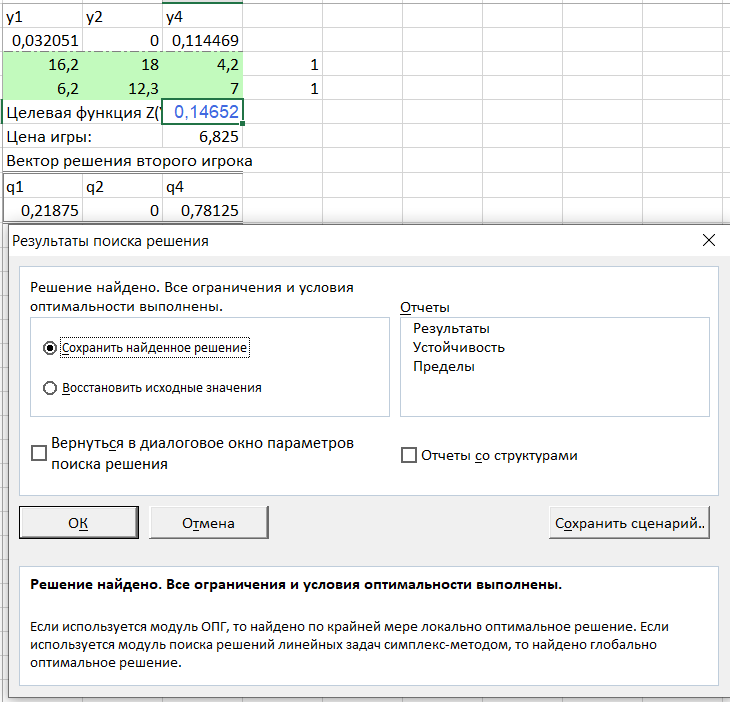
Рисунок 20 - Проверка результатов в программе Excel
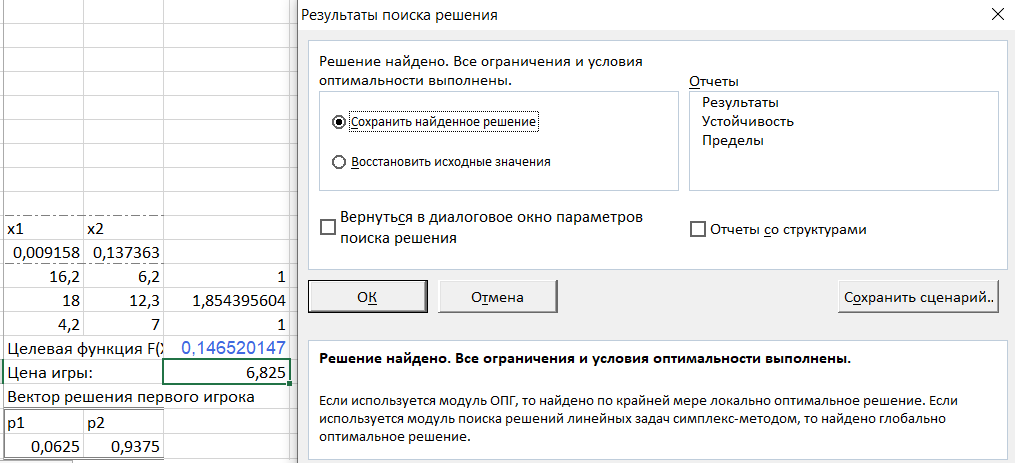
Рисунок 21 - Проверка результатов в программе Excel
