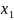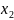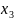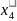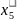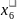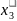1

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное автономное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

Кафедра 41

ПРЕПОДАВАТЕЛЬ

Ст. преподаватель				Б. К. Акопян
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

Лабораторная работа 1

Нахождение оптимального решения задачи линейного программирования симплекс-методом

по курсу: Прикладные методы оптимизации

СТУДЕНТКА ГР. №		Z0411		31.05.24		М. В. Карелина
	номер группы			подпись, дата		инициалы, фамилия

Номер студенческого билета: 2020/3477

Санкт-Петербург

2024

Вариант 8.

Пусть дана следующая задача:

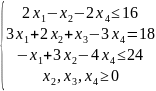
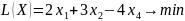
Необходимо найти такие значения переменных, при которых целевая функция L(X) будет минимизирована.

Решение: поставленная задача не приведена к канонической форме, поскольку система ограничений состоит из неравенств, а также не имеет начального опорного решения с базисом из единичных векторов. Методом введения искусственного базиса задача приводится к канонической форме:

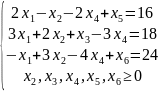
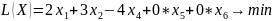
Данные сводятся в симплекс-таблицу (табл. 1), в столбце С^Б которой находятся коэффициенты базисных переменных. Симплекстаблица также известна как таблица Гаусса. Базисными переменными являются введенные искусственно переменные x₄ – x₆, отсюда начальное опорное решение:

x⁰ = (0;0;0;0;16;24)

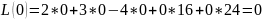
Таблица 1 - Симплекс-таблица

Базис	СБ	2		3		0		-4		0		0		bi		θi		Комм.
	0	3		2		1		-3		0		0		18
	0	2		-1		0		-2		1		0		16
	0	-1		3		0		-4		0		1		24
Δi			-2		-3		0		4		0		0		0		L = 0

Сосотавив симплекс-таблицу и проанализировав условия (Рис. 1)стало понятно что задача не имеет решения.

Рисунок 1. Условия проверки на оптимальность

Вывод

В ходе данной работы мы привели указанную систему методом введения искусственного базиса задача приводится к канонической форме:

В ходе создания и преобразования симплекс-таблицы было выявлено, что конечных неотрицательных отношений нет. Решения не существует. Целевая функция может быть сколь угодно маленькой.