3

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное автономное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

Кафедра 41

ПРЕПОДАВАТЕЛЬ

Ст. преподаватель				Б. К. Акопян
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

Лабораторная работа 3

Позиционные игры

по курсу: Прикладные методы оптимизации

СТУДЕНТКА ГР. №		Z0411		31.05.24		М. В. Карелина
	номер группы			подпись, дата		инициалы, фамилия

Номер студенческого билета: 2020/3477

Санкт-Петербург

2024

Цель работы:

изучить процесс нормализации позиционной игры.

Задание:

произвести нормализацию позиционной игры согласно варианту.

Вариант 8.

Опишем каждый ход игры.

Первый ход делает игрок А: выбирает значение для x из множества {1, 2, 3}.

Второй ход делает игрок В: выбирает значение для y из множества {1, 2}, если на прошлом ходе был выбран x = 1, 2 или 3.

Третий ход делает игрок А: он помнит и свой первый шаг и шаг игрока В, поэтому выбор значения для числа z (из множества {1, 2} при x ∈ {1, 3}) будет основан на этой информации. Игрок В имеет следующие стратегии:

В1 – ([1, 1, 1]), В2 – ([2, 1, 2]), В3 – ([1, 1, 2]), В4 – ([2, 1, 1]).

Игрок А имеет следующие стратегии:

А1 – (1, [1, 1]), А2 – (1, [1, 2]), А3 – (1, [2, 1]). А4 – (1, [2, 2]),

А5 – (2, [1, 1]), А6 – (2, [1, 2]), А7 – (2, [2, 1]), А8 – (2, [2, 2]),

А9 – (3, [1, 1]), А10 – (3, [1, 2]), А11 – (3, [2, 1]), А12 – (3, [2, 2]).

Выигрыш игрока А можно определить при помощи функции W(x, y, z).

На основе полученных значений составим таблицу выигрышей игрока А и матрицу игры:

		B1	B2	B3	B4
		[1, 1, 1]	[2, 1, 2]	[1, 1, 2]	[2, 1, 1]
A1	(1, [1, 1])	W(1, 1, 1)	W(1, 2, 1)	W(1, 1, 1)	W(1, 2, 1)
A2	(1, [1, 2])	W(1, 1, 1)	W(1, 2, 2)	W(1, 1, 1)	W(1, 2, 2)
A3	(1, [2, 1])	W(1, 1, 2)	W(1, 2, 1)	W(1, 1, 2)	W(1, 2, 1)
A4	(1, [2, 2])	W(1, 1, 2)	W(1, 2, 2)	W(1, 1, 2)	W(1, 2, 2)
A5	(2, [1, 1])	W(2, 1, 1)	W(2, 2, 1)	W(2, 2, 1)	W(2, 1, 1)
A6	(2, [1, 2])	W(2, 1, 1)	W(2, 2, 2)	W(2, 2, 2)	W(2, 1, 1)
A7	(2, [2, 1])	W(2, 1, 2)	W(2, 2, 1)	W(2, 2, 1)	W(2, 1, 2)
A8	(2, [2, 2])	W(2, 1, 2)	W(2, 2, 2)	W(2, 2, 2)	W(2, 1, 2)
A9	(3, [1, 1])	W(3, 1, 1)	W(3, 2, 1)	W(3, 2, 1)	W(3, 1, 1)
A10	(3, [1, 2])	W(3, 1, 1)	W(3, 2, 2)	W(3, 2, 2)	W(3, 1, 1)
A11	(3, [2, 1])	W(3, 1, 2)	W(3, 2, 1)	W(3, 2, 1)	W(3, 1, 2)
A12	(3, [2, 2])	W(3, 1, 2)	W(3, 2, 2)	W(3, 2, 2)	W(3, 1, 2)

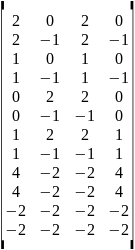
Применяем отношения доминирования. Для игрока В исключаются столбцы, все элементы которых больше соответствующих им на данной строке элементов другого столбца. Для игрока А исключаются строки, все элементы которых меньше соответствующим им в данном столбце элементов другой строки. После применения отношений доминирования в матрице игры остается седьмая строка.

Полученная оптимальная стратегия игрока А – A₇ (2, [2, 1]), игрока В – В₁, В₂, В₃, В₄.

Цена игры v = 1,2.