2

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное автономное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

Кафедра 41

ПРЕПОДАВАТЕЛЬ

Ст. преподаватель				Б. К. Акопян
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

Лабораторная работа 2

Принятие решений в условиях неопределенности. Игры с природой

по курсу: Прикладные методы оптимизации

СТУДЕНТКА ГР. №		Z0411		31.05.24		М. В. Карелина
	номер группы			подпись, дата		инициалы, фамилия

Номер студенческого билета: 2020/3477

Санкт-Петербург

2024

Цель: освоить и закрепить практические навыки по принятию и обоснованию решений в условиях недостатка информации, когда один из игроков не имеет конкретной цели и случайным образом выбирает очередные «ходы».

Задание: определить наилучшую стратегию для игрока по заданной в соответствии с вариантом платежной матрице.

Вариант 8.

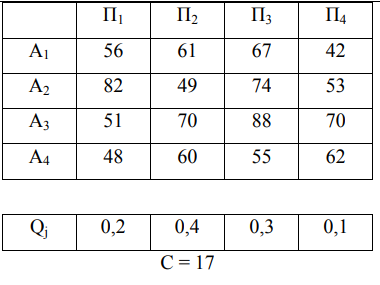
Требуется выбрать такую стратегию игрока, которая является более предпочтительной (выгодной) по сравнению с другими. Прежде чем приступить к решению, необходимо удалить заведомо невыгодные или дублирующие стратегии игрока А. Что же касается стратегий «природы», то здесь заведомо невыгодные стратегии удалять нельзя, так как «природа» свои стратегии не выбирает.

Задана матрица A. Все критерии будут рассмотрены на основе нее:

Рассмотрим заданную матрицу на наличие невыгодных или дублирующих стратегий игрока. Из матрицы видно, что таких стратегий нет.

С целью описания степени удачности применения конкретной стратегии в конкретной ситуации с учетом того, насколько вообще эта ситуация благоприятна для нас вводится понятие «риска». Риск описывается следующей формулой: r_ij = b_j – a_ij , где b_j = max a_ij.

Таким образом матрица риска по заданной матрице A примет следующий вид:

1. Максиминный критерий Вальда

Этот критерий отражает принцип гарантированного результата, т. е. игрок выбирает такую стратегию, которая максимизировала бы его выигрыш в самой неблагоприятной ситуации.

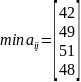
По критерию Вальда лучшая стратегия номер 3, т.к. решение игрока будет наиболее выигрышным, даже при наихудших условиях.

2. Критерий минимаксного риска Сэвиджа

Критерий минимаксного риска Сэвиджа предполагает, что оптимальной является та стратегия, при которой величина риска в наихудшем случае минимальна.

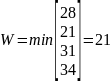
По данному критерию получается, что лучшая стратегия 2, при ней будут наименьшие риски.

3. Критерий пессимизма-оптимизма Гурвица

Критерий рекомендует при выборе решения не руководствоваться ни крайним пессимизмом, ни крайним оптимизмом.

, где γ – степень пессимизма, определяется в диапазоне [0, 1].

При γ = 1 – пессимистический критерий Вальда. При γ = 0 – критерий максимума. Выбор конкретного значения параметра определяется, скорее всего, субъективными факторами: чем опаснее ситуация, тем больше надо «подстраховываться» и тем ближе к единице выбирается значение γ.

Примем γ = 0,5.

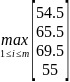= =69.5

Примем γ = 0,3.

= =76.9

Примем γ = 0,7.

= =62.1

По данному критерию стоит выбрать 3 стратегию.

4. Критерий Лапласа

При неизвестных вероятностях состояний «природы» можно принять, что все они равновероятны и применить критерий Лапласа.

=

Согласно данному критерию, стоит выбрать 3 стратегию.

5. «Идеальный» эксперимент

«Идеальным» называется эксперимент, который приводит к точному знанию состояния «природы», которое имеет место в данной ситуации. В данном эксперименте известно следующее:

 Матрица выигрышей А;

 вероятности Q1, ..., Qn различных состояний «природы» П1, ..., Пn, сумма Q не должна превышать 1;

 затраты С на проведение эксперимента ξ.

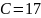
Построим матрицу рисков.

Из расчетов видно, что эксперимент нецелесообразно проводить. Стоит выбрать 3 стратегию, так как достигается минимум среднего риска.

Вывод

В данной работе мы освоили и закрепили практические навыки по принятию и обоснованию решений в условиях недостатка информации, когда один из игроков не имеет конкретной цели и случайным образом выбирает очередные «ходы», а именно определили наилучшую стратегию для игрока по заданной в соответствии с вариантом платежной матрице.

На основе данной матрицы были рассчитаны:

• максиминный критерий Вальда - по критерию Вальда лучшая стратегия номер 3;

• критерий минимаксного риска Сэвиджа, который показал, что лучшая стратегия 2;

• критерий пессимизма-оптимизма Гурвица, который при разных степенях пессимизма показал наилучшей 3 стратегию;

• критерий Лапласа, по которому лучшая стратегия 3

• расчеты для идеального эксперимента показали, что его нецелесообразно проводить, но стоит выбрать 3 стратегию, так как достигается минимум среднего риска.

Беря в расчет данные критерии, можно сказать, что 3 стратегия является наиболее выигрышной.