4

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное автономное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

Кафедра 41

ПРЕПОДАВАТЕЛЬ

Проф., д.-р физ.-мат. наук				Ю. В. Рождественский
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

Лабораторная работа №4

Моделирование одноканальной системы массового обслуживания с конечной очередью

по курсу: Имитационное моделирование

СТУДЕНТКА ГР. №		Z0411		05.02.25		М. В. Карелина
	номер группы			подпись, дата		инициалы, фамилия

Номер студенческого билета: 2020/3477

Санкт-Петербург

2025

Цель работы:

1. Провести моделирование входного потока событий - простейший поток, поток Эрланга k-порядка на выбор;

2. Получить выходной поток и исследовать его характеристики;

3. Исследовать пропускную способность системы в зависимости от интенсивности входного потока.

Ход работы:

Системы массового обслуживания (СМО) широко применяются для моделирования различных процессов в телекоммуникациях, логистике, экономике и других областях. В данной работе рассматривается одноканальная СМО с конечной очередью. Очередь ограничена по размеру, что означает возможность потерь заявок при переполнении.

Входной поток может описываться:

• Простейшим потоком (пуассоновский поток), при котором время между поступлениями заявок распределено экспоненциально.

• Потоком Эрланга порядка k, который является частным случаем гамма-распределения и более детально моделирует процессы с фазами ожидания.

Обслуживание заявок осуществляется в порядке FIFO (первый пришёл – первый обслужен), а время обслуживания подчиняется экспоненциальному распределению.

Для моделирования системы используется библиотека SimPy. Основные параметры модели:

• Интенсивность входного потока (λ) – среднее число заявок, поступающих в систему за единицу времени.

• Интенсивность обслуживания (μ) – среднее число заявок, обрабатываемых сервером за единицу времени.

• Размер очереди – максимальное количество заявок, которые могут находиться в очереди.

• Время моделирования – общее время, в течение которого система функционирует.

Процесс моделирования включает:

1. Генерацию входного потока заявок.

2. Обработку заявок сервером.

3. Фиксацию обработанных и потерянных заявок.

4. Вычисление характеристик выходного потока (среднее время ожидания, пропускная способность и т. д.).

Для исследования системы моделирование проводилось для различных значений интенсивности входного потока (λ = 2, 4, 6, 8, 10, 12, 16 заявок/единицу времени) при фиксированной интенсивности обслуживания (μ = 4 заявок/единицу времени). Размер очереди был установлен в 2 мест, а время моделирования – 500 единиц времени. В качестве входного потока использовался поток Эрланга порядка 3.

В ходе моделирования были получены графики плотности вероятности Эрланговского потока, распределения времени обслуживания заявок и событийного графика, отображающего моменты прихода, начала обслуживания и выхода заявок из системы.

Моделирование проводилось с использованием программного кода на языке Python, который представлен в Листинге 1.

import numpy as np import simpy import matplotlib.pyplot as plt class QueueSystem: def __init__(self, env, service_rate, queue_size, arrival_rate, erlang_k=3): self.env = env self.server = simpy.Resource(env, capacity=1) # Одна служба self.queue_size = queue_size # Максимальная длина очереди self.service_rate = service_rate # Интенсивность обслуживания self.arrival_rate = arrival_rate # Интенсивность входного потока self.erlang_k = erlang_k # Порядок Эрланга # Статистика self.processed = 0 self.lost = 0 self.wait_times = [] self.service_times = [] self.timestamps = [] def arrival_process(self): while True: # Генерация времени между прибытием с использованием распределения Эрланга interarrival_time = np.random.gamma(self.erlang_k, 1 / (self.arrival_rate / self.erlang_k)) yield self.env.timeout(interarrival_time) # Задержка перед прибытием self.env.process(self.handle_request()) def handle_request(self): arrival_time = self.env.now self.timestamps.append((arrival_time, 'arrival')) if len(self.server.queue) < self.queue_size: with self.server.request() as request: yield request # Ожидаем, пока служба будет доступна service_time = np.random.exponential(1 / self.service_rate) # Время обслуживания self.service_times.append(service_time) start_service_time = self.env.now self.timestamps.append((start_service_time, 'service')) yield self.env.timeout(service_time) # Задержка на обслуживание self.wait_times.append(self.env.now - arrival_time) # Записываем время ожидания self.processed += 1 self.timestamps.append((self.env.now, 'departure')) else: self.lost += 1 # Увеличиваем счетчик потерянных клиентов # Параметры моделирования arrival_rates = [1, 2, 4, 8, 16] # Различные интенсивности входного потока service_rate = 4 # Интенсивность обслуживания queue_size = 2 # Максимальная длина очереди simulation_time = 500 # Время моделирования # Запуск симуляции for arrival_rate in arrival_rates: env = simpy.Environment() system = QueueSystem(env, service_rate, queue_size, arrival_rate, erlang_k=3) env.process(system.arrival_process()) env.run(until=simulation_time) # Нижняя статистика throughput = system.processed / simulation_time # Пропускная способность avg_requests_per_time = (system.processed + system.lost) / simulation_time # Среднее количество заявок в системе # Отчет о результатах print(f"\nИнтенсивность входного потока: {arrival_rate}") print(f"Обработано заявок: {system.processed}") print(f"Потеряно заявок: {system.lost}") print(f"Среднее время ожидания: {np.mean(system.wait_times) if system.wait_times else 0:.2f}") print(f"Мощность выходного потока: {throughput:.2f} заявок/ед. времени") print(f"Среднее количество заявок в системе: {avg_requests_per_time:.2f} заявок/ед. времени") # Графики плотности вероятности Эрланговского потока x = np.linspace(0, 5, 1000) plt.figure(figsize=(10, 5)) for arrival_rate in arrival_rates: erlang_pdf = (arrival_rate**2 * x * np.exp(-arrival_rate * x)) / 1 # k=2 plt.plot(x, erlang_pdf, label=f'Эрланг (λ={arrival_rate}, k=2)', linewidth=2) # Находим пики и отображаем их peak = np.max(erlang_pdf) peak_x = x[np.argmax(erlang_pdf)] plt.scatter(peak_x, peak, color='red', marker='o') # Отображение пиков # Добавляем аннотацию для координат пиков plt.annotate(f'({peak_x:.2f}, {peak:.2f})', xy=(peak_x, peak), xytext=(peak_x + 0.5, peak - 0.05), # Положение текста arrowprops=dict(facecolor='black', arrowstyle='->')) # Стиль стрелки plt.xlabel('Время между заявками', fontsize=12) plt.ylabel('Плотность вероятности', fontsize=12) plt.legend() plt.title("График плотности вероятности Эрланговского потока", fontsize=14) plt.grid(color='gray', linestyle='--', linewidth=0.5) # Добавляем сетку plt.gca().set_facecolor('#f2f2f2') # Добавляем светлый фон к графику plt.show() # График распределения времени обслуживания service_times = np.random.exponential(1 / service_rate, 1000) plt.figure(figsize=(10, 5)) plt.hist(service_times, bins=30, density=True, alpha=0.6, color='coral', edgecolor='black', label='Экспоненциальное распределение') plt.xlabel('Время обслуживания', fontsize=12) plt.ylabel('Плотность вероятности', fontsize=12) plt.legend() plt.title("График закона распределения вероятностей для времени обслуживания заявок", fontsize=14) plt.grid(color='gray', linestyle='--', linewidth=0.5) # Добавляем сетку plt.gca().set_facecolor('#f2f2f2') # Добавляем светлый фон к графику plt.show() # Событийные графики для разных arrival_rates for arrival_rate in arrival_rates: env = simpy.Environment() system = QueueSystem(env, service_rate, queue_size, arrival_rate, erlang_k=2) env.process(system.arrival_process()) env.run(until=simulation_time) timestamps = sorted(system.timestamps) timestamps = [t for t in timestamps if t[0] <= 25] # Ограничение по времени до 25 if timestamps: time, events = zip(*timestamps) levels = {'arrival': 3, 'service': 2, 'departure': 1} y_positions = [levels[event] for event in events] plt.figure(figsize=(12, 5)) plt.scatter(time, y_positions, marker='o', color='r', label='События') for i in range(len(time) - 1): plt.plot([time[i], time[i]], [y_positions[i], y_positions[i + 1]], 'k-', alpha=0.5) plt.xlabel('Время') plt.yticks([1, 2, 3], ['Выход', 'Обслуживание', 'Вход']) plt.legend() plt.title(f"Событийный график (вход, обслуживание, выход) для λ={arrival_rate}") plt.show()

Результаты выполнения программного кода представлены на Рисунках 1-5.

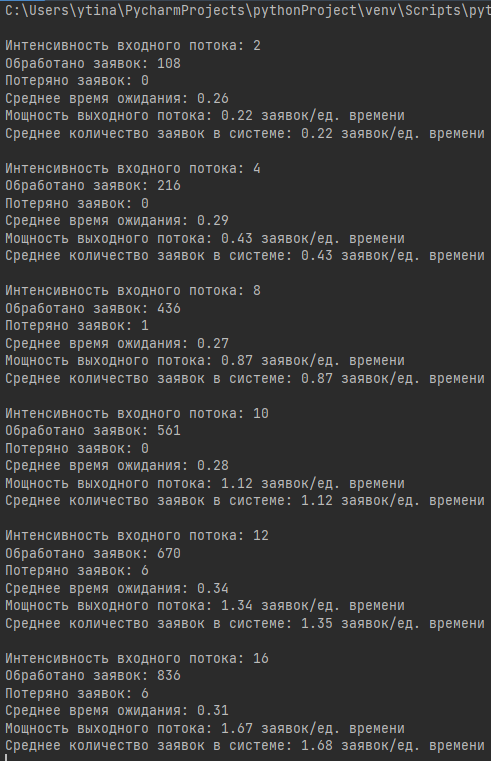
Рисунок 1 - Расчет параметров СМО

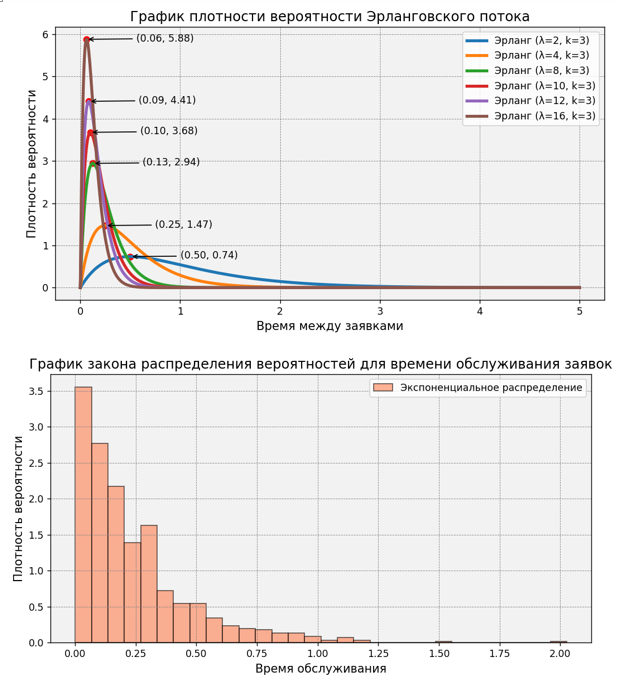
Рисунок 2 - Графики плотности вероятности Эрланговского потока и закона распределения вероятностей для времени обслуживания заявок

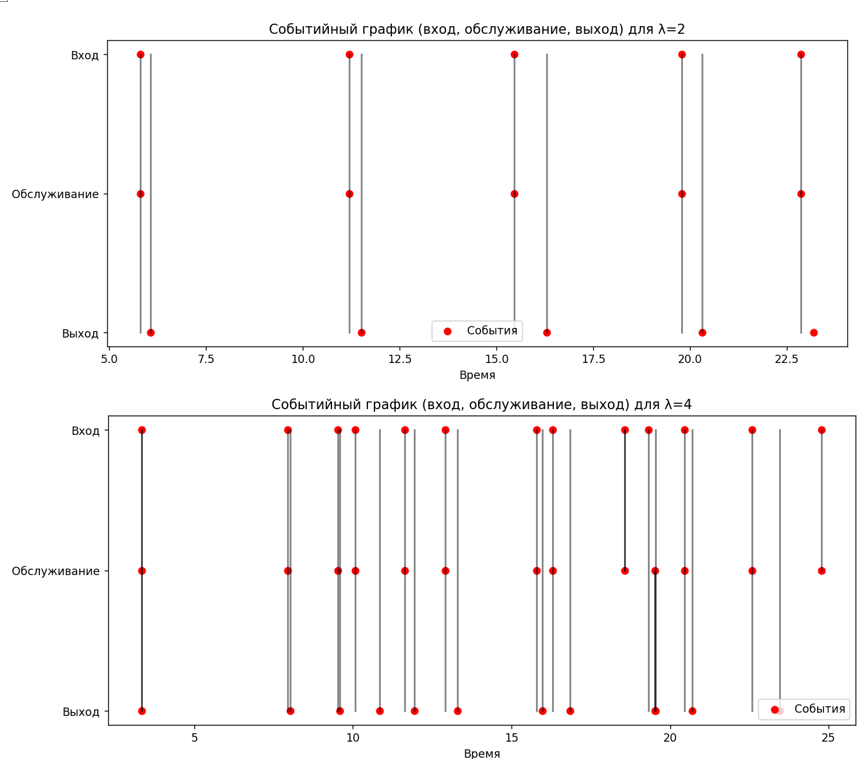
Рисунок 3 - Событийные графики для входных потоков 2 и 4

Рисунок 4 - Событийные графики для входных потоков 8 и 10

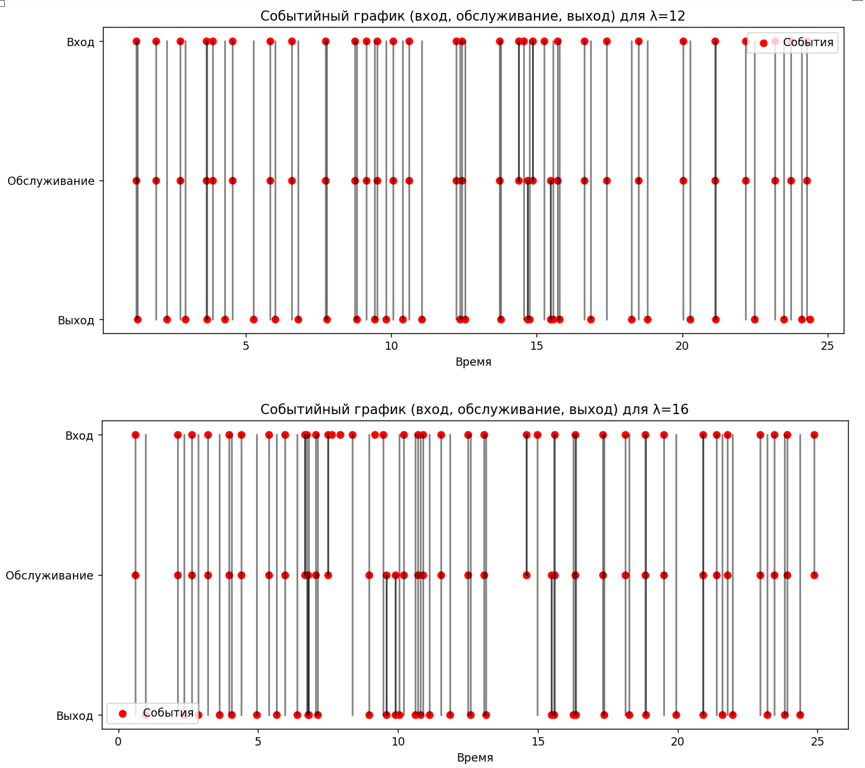
Рисунок 5 - Событийные графики для входных потоков 12 и 16

В процессе моделирования были выявлены зависимости между характеристиками выходного потока и интенсивностью входящего потока. К основным выводам можно отнести следующее:

1. Зависимость между интенсивностью и пропускной способностью: Увеличение интенсивности входного потока λ приводит к росту пропускной способности системы до определенного предела. Однако, после достижения этого порога происходит значительное увеличение потерь заявок, что связано с ограничениями очереди.

2. Возрастание среднего времени ожидания: Время ожидания заявок увеличивается пропорционально росту входного потока. Это объясняется тем, что сервер сталкивается с более высокой загрузкой и быстрее заполняется очередь, что замедляет обработку заявок.

3. Плотность вероятности потоков Эрланга: Анализ графиков плотности вероятности показывает, что с увеличением λ вероятность коротких интервалов между поступающими заявками возрастает, что указывает на более частое наличие коротких ожиданий.

4. Экспоненциальное распределение времени обслуживания: График, представляющий распределение времени обслуживания, подтверждает экспоненциальный характер процесса, что соответствует используемой модели обслуживания и ее параметрам.

5. Способы визуализации обработки заявок: Событийный график ясно иллюстрирует последовательность обработки заявок, что дополнительно подтверждает правильность проведенного моделирования.

Вывод

В ходе выполнения лабораторной работы была смоделирована одноканальная система массового обслуживания с конечной очередью, где входной поток заявок описывался потоком Эрланга порядка k=3. Были проанализированы характеристики системы, включая пропускную способность, среднее время ожидания и плотность вероятности времени между заявками. Полученные результаты подтверждают теоретические ожидания: при увеличении интенсивности входного потока нагрузка на систему возрастает, что приводит к увеличению времени ожидания и возможным потерям заявок. Модель, реализованная с использованием SimPy, продемонстрировала свою применимость для анализа систем массового обслуживания и может быть использована для оптимизации их параметров.