2

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное автономное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

Кафедра 41

ПРЕПОДАВАТЕЛЬ

Проф., д.-р физ.-мат. наук				Ю. В. Рождественский
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

Лабораторная работа №2

Генератор равномерно распределенных случайных чисел

по курсу: Имитационное моделирование

СТУДЕНТКА ГР. №		Z0411		03.02.2025		М. В. Карелина
	номер группы			подпись, дата		инициалы, фамилия

Номер студенческого билета: 2020/3477

Санкт-Петербург

2025

Цель работы: реализовать собственный генератор случайных чисел, равномерно распределенных на отрезке от 0 до 1. Исследовать генератор на равномерность

Ход работы:

Генераторы псевдослучайных чисел (ГПСЧ) играют важную роль в имитационном моделировании различных событий, поскольку они позволяют создавать последовательности чисел для моделирования случайных процессов и явлений. ГПСЧ используются для генерации случайных значений параметров системы, что позволяет учесть неопределённость и случайность в реальных системах и получить более точные результаты. При создании генератора был использованы методы Нормализации и Сглаживания значений. Каждые 1000 сгенерированных значений 10% из них уменьшаются на 10%, чтобы создать эффект аккуратного распределения.

Программный код моего генератора псевдослучайных чисел представлен в листинге 1.

Листинг 1.

import numpy as np import matplotlib.pyplot as plt import seaborn as sns class UniformRandomNumberGenerator: def __init__(self, seed=None): if seed is not None: np.random.seed(seed) def generate_uniform_random(self, size=1): """Генерация случайных чисел с равномерным распределением на отрезке [0, 1]""" samples = [] for i in range(size): number = np.random.uniform(0, 1) # Нормализация значений samples.append(np.clip(number, 0, 1)) # Каждые 1000 значений, сглаживание 10% из них if (i + 1) % 1000 == 0: adjust_count = int(0.1 * 1000) # 10% из 1000 for j in range(adjust_count): samples[-(adjust_count - j)] *= 0.9 # Сглаживание, уменьшение на 10% samples[-(adjust_count - j)] = np.clip(samples[-(adjust_count - j)], 0, 1) return samples def plot_density(samples): """Создание графика плотности распределения""" plt.figure(figsize=(10, 5)) sns.kdeplot(samples, fill=True, color='blue', bw_adjust=0.5) plt.title("Плотность распределения случайных чисел") plt.xlabel("Значение") plt.ylabel("Плотность") plt.xlim(0, 1) plt.grid() plt.show() def plot_2d_distribution(x_samples, y_samples): """Создание цветного двумерного распределения""" plt.figure(figsize=(6, 6)) plt.hexbin(x_samples, y_samples, gridsize=50, cmap='viridis', mincnt=1) # Используем цветовую градацию plt.colorbar(label='Количество точек') plt.title("Двумерное распределение случайных чисел") plt.xlabel("X-координата") plt.ylabel("Y-координата") plt.xlim(0, 1) plt.ylim(0, 1) plt.grid() plt.show() def main(): num_samples = 100000 rng = UniformRandomNumberGenerator(seed=42) # Задаем seed для воспроизводимости # Генерация 100000 случайных чисел с равномерным распределением samples = rng.generate_uniform_random(num_samples) # Визуализация плотности plot_density(samples) # Генерация двумерных случайных чисел x_samples = rng.generate_uniform_random(num_samples) y_samples = rng.generate_uniform_random(num_samples) # Визуализация цветного двумерного распределения plot_2d_distribution(x_samples, y_samples) if __name__ == "__main__": main()

График плотности распределения случайных величин представлен на Рисунке 1.

Рисунок 1 - График плотности распределения

Визуализация попаданий точек на двумерном поле представлена на Рисунке 2.

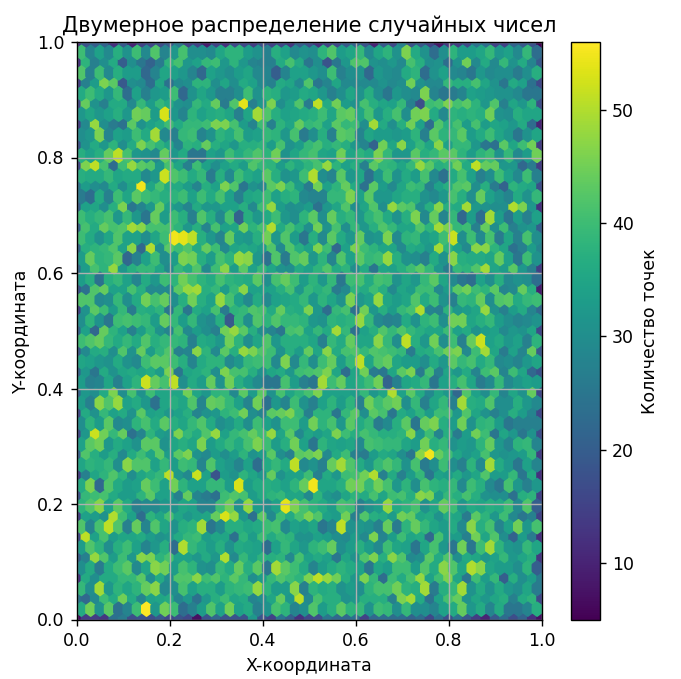
Рисунок 2 - График двумерного распределения случайных чисел

Изучая результаты работы генератора случайных чисел и график плотности распределения величин, можно считать его реализацию вполне удовлетворительной. В следующей лабораторной работе мой генератор будет также использован для нахождения числа π методом Монте-Карло.

Вывод

В результате работы над созданием генератора случайных чисел были достигнуты следующие цели и выводы:

Генератор предназначен для создания равномерно распределённых случайных чисел на отрезке [0, 1]. Этот диапазон позволяет обеспечить синтетические выборки, которые можно использовать в различных областях, таких как статистическое моделирование, симуляции и машинное обучение.

В процессе разработки были внедрены два основных правила:

- Нормализация значений: Все сгенерированные значения нормализуются, чтобы гарантировать, что они всегда остаются в пределах от 0 до 1.

- Сглаживание значений: Каждые 1000 сгенерированных чисел 10% их значений подвергаются уменьшению, что помогает создавать более сбалансированное распределение, избегая резких пиков.

Генератор включает в себя две функции визуализации:

- График плотности: Используется для отображения распределения сгенерированных случайных чисел, где растяжение значений указывает на преобладание определённых значений.

- Цветное двумерное распределение: Отображает концентрацию значений в виде тепловой карты, что наглядно демонстрирует, как величины распределяются по двум измерениям. Использование цветовой градации позволяет лучше понять области с высокой или низкой плотностью значений.

Создание генератора случайных чисел стало полезным упражнением, которое продемонстрировало важность разнообразных техник нормализации и распределения. Выводы, полученные в ходе работы, могут быть эффективно применены в различных научных и практических областях, требующих случайного моделирования или анализа данных. С помощью визуализаций стало легче понять распределение и структуру этих значений, что может быть полезно для дальнейшего анализа и принятия решений.