
2
.docxМИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное автономное образовательное учреждение высшего образования
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»
Кафедра 41
ПРЕПОДАВАТЕЛЬ
доц., к.т.н., доц. |
|
|
|
О. О. Жаринов |
должность, уч. степень, звание |
|
подпись, дата |
|
инициалы, фамилия |
Лабораторная работа №2
Основы обработки аудиосигналов средствами Python. Метод фильтрации в спектральном пространстве
по курсу: Мультимедиа технологии
СТУДЕНТКА ГР. № |
Z0411 |
|
01.04.25 |
|
М. В. Карелина |
|
|
номер группы |
|
подпись, дата |
|
инициалы, фамилия |
|
Номер студенческого билета: 2020/3477
Санкт-Петербург
2025
Цель работы: изучить основы обработки аудиосигналов на примере метода фильтрации сигналов в спектральном пространстве.
Вариант 7 приведён в таблице 1.
Таблица 1 – Индивидуальный вариант задания
Вариант |
Тип фильтра |
Граничные частоты полосы пропуская фильтра |
|
|
|
||
7 |
Фильтр нижних частот |
− |
600 |
Для выполнения задания создадим сигнал с частотой дискретизации (Fs) в 44100 Гц и длительностью в 5 секунд. Данный код генерирует звуковую волну от 100 гц до 1500 гц в котором частота постепенно увеличивается от заданного начального до конечного значения с диапазоном в 150 Гц. Сохранение производится под наименованием LR2 и в формате wav. Программный код представлен в листинге 1.
Листинг 1. Создание аудиосигнала
import numpy as np from scipy.io.wavfile import write # Параметры аудиосигнала Fs = 44100 # частота дискретизации duration = 5 # длительность в секундах t = np.linspace(0, duration, int(Fs * duration), endpoint=False) # Параметры частоты start_freq = 100 # начальная частота end_freq = 1500 # конечная частота freq_range = 150 # ширина диапазона частот # Генерация сигнала current_frequencies = np.linspace(start_freq, end_freq, len(t)) # Линейное распределение частот freq_centers = current_frequencies[:, np.newaxis] + np.arange(-freq_range // 2, freq_range // 2 + 1, 10) # Центры частот signal_sweep = np.sum(np.sin(2 * np.pi * freq_centers * t[:, np.newaxis]), axis=1) # Генерация сигнала # Нормализация сигнала signal_sweep = np.int16((signal_sweep / np.max(np.abs(signal_sweep))) * 32767) # Запись в файл filename_sweep = 'LR2.wav' write(filename_sweep, Fs, signal_sweep) |
Фильтр нижних частот (ФНЧ) — это фильтр, который позволяет пропускать сигналы с частотами ниже заданной границы (пороговой частоты) и attenuate (ослаблять) сигналы с частотами выше этой границы.
Для иллюстрации работы с фильтром нижних частот был использован ранее созданный сигнал LR2. Программный код представлен в листинге 2. После выполнения программы происходит визуализация сигнала с фильтром и без на рисунках 1-5.
Листинг 2. Обработка и визуализация сигнала
import numpy as np import matplotlib.pyplot as plt from scipy.fft import fft, ifft from scipy.io import wavfile # Чтение файла lr2.wav sampling_rate, signal = wavfile.read('LR2.wav') signal = signal.astype(float) # Преобразование Фурье spectrum = fft(signal) frequencies = np.fft.fftfreq(len(signal), 1/sampling_rate) # Фильтр нижних частот upper_bound = 600 filter_mask = np.ones_like(frequencies, dtype=bool) filter_mask[np.abs(frequencies) > upper_bound] = False filtered_spectrum = spectrum * filter_mask # Обратное преобразование Фурье filtered_signal = ifft(filtered_spectrum).real # Визуализация сигнала без фильтра plt.figure(figsize=(10, 5)) plt.plot(signal / np.max(np.abs(signal)), color='green', label='Исходный сигнал') plt.title('Исходный сигнал') plt.xlabel('Время') plt.ylabel('Амплитуда') plt.legend() plt.grid(True) plt.show() plt.figure(figsize=(10, 5)) plt.plot(frequencies, np.abs(spectrum) / np.max(np.abs(spectrum)), color='green', label='Спектр исходного сигнала') plt.title('Спектр исходного сигнала') plt.xlabel('Частота') plt.ylabel('Амплитуда') plt.legend() plt.grid(True) plt.show() # Визуализация отфильтрованного сигнала plt.figure(figsize=(10, 5)) plt.plot(filtered_signal, color='green', label='Отфильтрованный сигнал') plt.title('Отфильтрованный сигнал') plt.xlabel('Время') plt.ylabel('Амплитуда') plt.legend() plt.grid(True) plt.show() plt.figure(figsize=(10, 5)) plt.plot(frequencies, np.abs(filtered_spectrum) / np.max(np.abs(filtered_spectrum)), color='green', label='Спектр отфильтрованного сигнала') plt.title('Спектр отфильтрованного сигнала') plt.xlabel('Частота') plt.ylabel('Амплитуда') plt.legend() plt.grid(True) plt.show() # Спектограмма до и после фильтрации plt.figure(figsize=(12, 6)) plt.subplot(2, 1, 1) plt.specgram(signal, NFFT=1024, Fs=sampling_rate, noverlap=512, cmap='hot') plt.title('Спектограмма исходного сигнала') plt.xlabel('Время') plt.ylabel('Частота') plt.subplot(2, 1, 2) plt.specgram(filtered_signal, NFFT=1024, Fs=sampling_rate, noverlap=512, cmap='hot') plt.title('Спектограмма отфильтрованного сигнала') plt.xlabel('Время') plt.ylabel('Частота') plt.tight_layout() plt.show() # Запись отфильтрованного сигнала в файл wavfile.write('LR2.1.wav', sampling_rate, (filtered_signal * 32767).astype(np.int16)) |

Рисунок 1 – Визуализация исходного сигнала
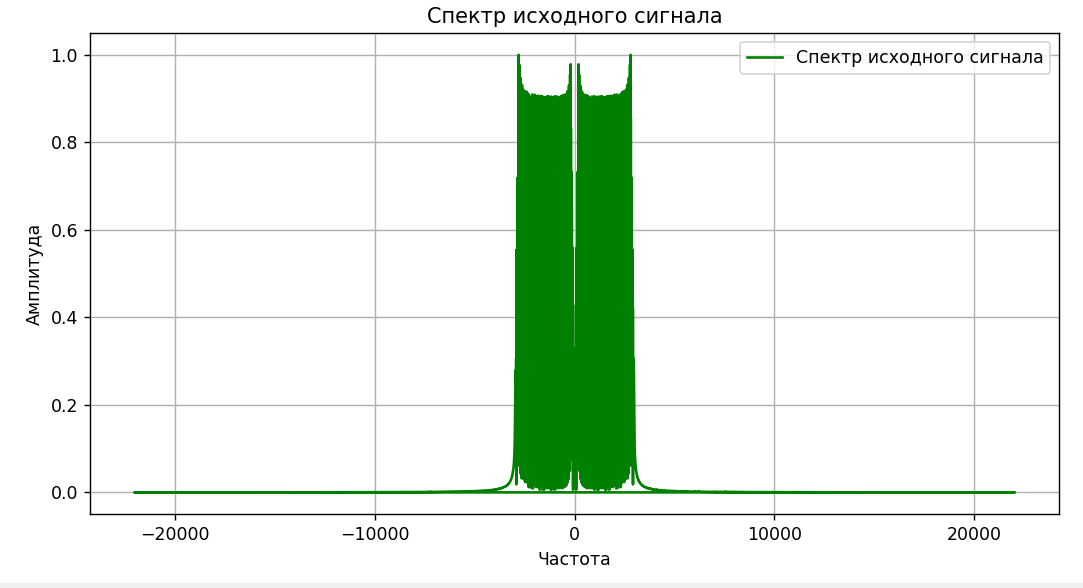
Рисунок
2 – Визуализация исходного сигнала
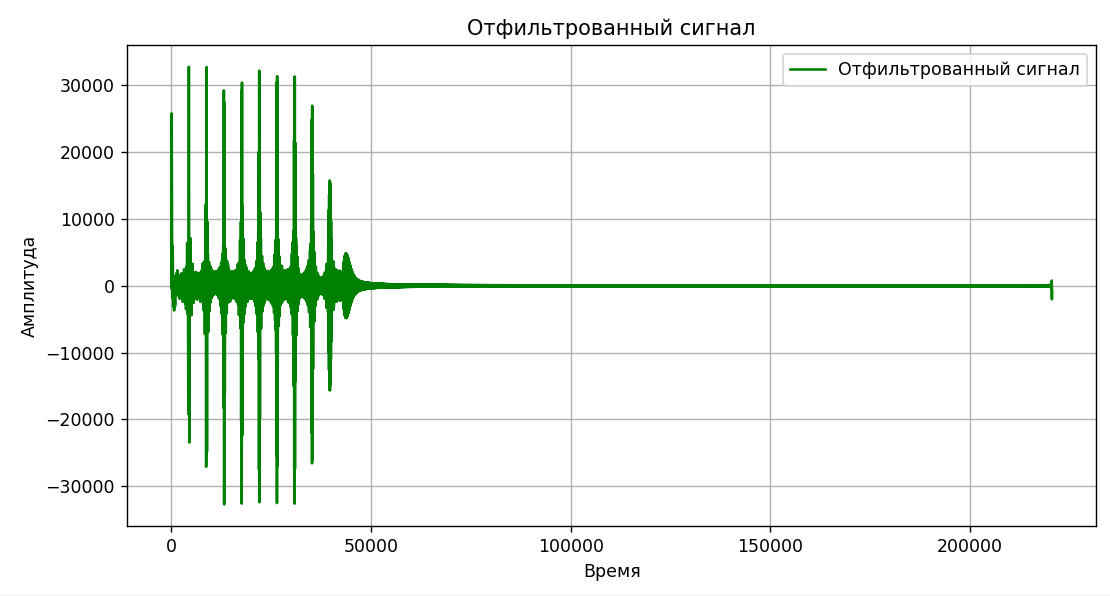
Рисунок 3 – Визуализация отфильтрованного сигнала
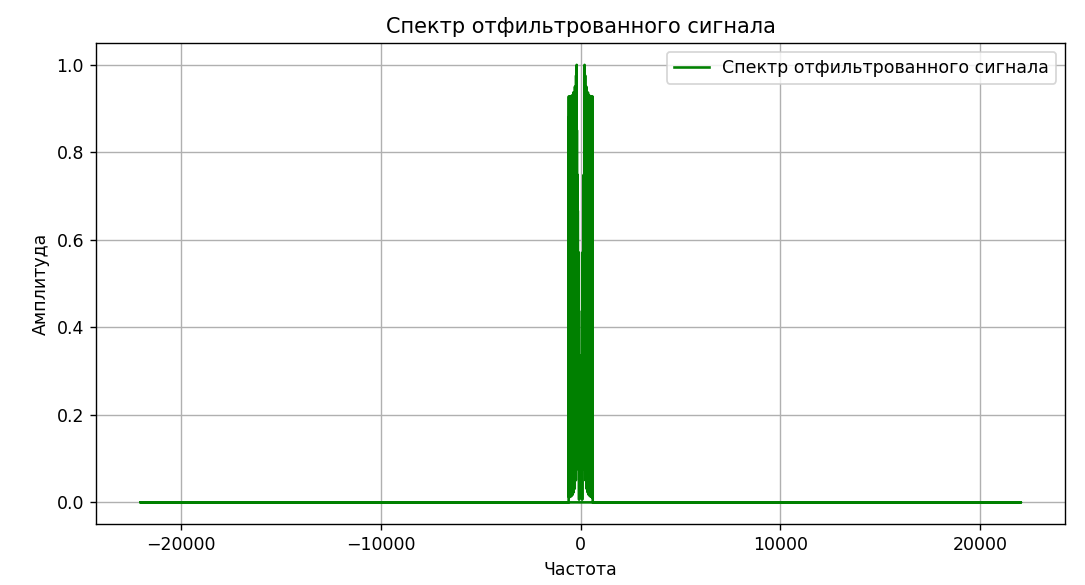
Рисунок
4 – Визуализация отфильтрованного
сигнала
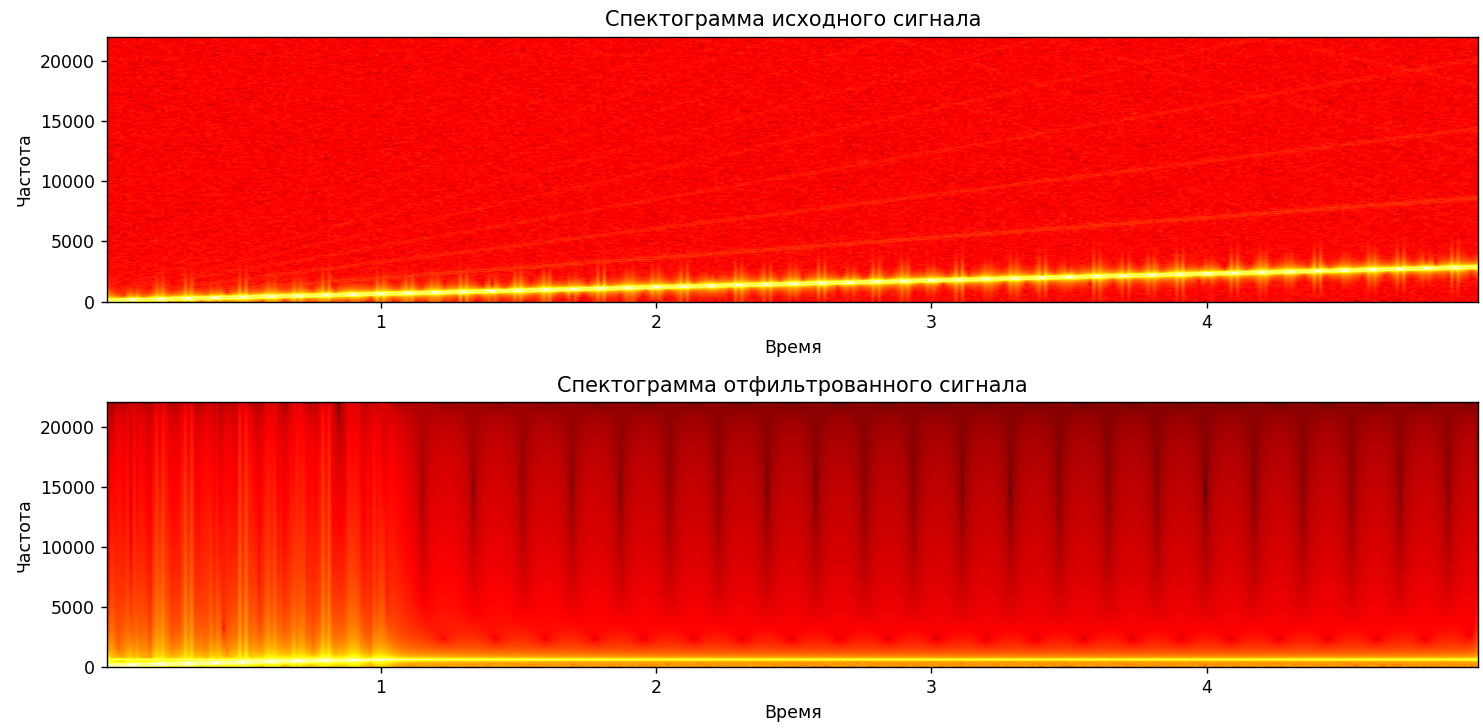
Рисунок 5 – Визуализация сигнала, спектрограмма, до и после применения фильтра
При прослушивании отфильтрованного сигнала были замечены изменения в худшую сторону, звук стал напоминать шипение и технический скрежет.
Далее переходим к обработке ранее загруженного файла с пением птиц с названием LR2MUSIC. Код программы представлен в Листинге 3.
Листинг 3. Обработка реальной композиции.
import numpy as np import matplotlib.pyplot as plt from scipy.fft import fft, ifft from scipy.io import wavfile # Чтение файла sampling_rate, signal = wavfile.read('LR2MUSIC.wav') signal = signal.astype(float) # Преобразование Фурье spectrum = fft(signal) frequencies = np.fft.fftfreq(len(signal), 1/sampling_rate) # Фильтр нижних частот upper_bound = 600 filter_mask = np.ones_like(frequencies, dtype=bool) filter_mask[np.abs(frequencies) > upper_bound] = False filtered_spectrum = spectrum * filter_mask # Обратное преобразование Фурье filtered_signal = ifft(filtered_spectrum).real # Визуализация сигнала без фильтра plt.figure(figsize=(10, 5)) plt.plot(signal / np.max(np.abs(signal)), color='green', label='Исходный сигнал') plt.title('Исходный сигнал') plt.xlabel('Время') plt.ylabel('Амплитуда') plt.legend() plt.grid(True) plt.show() plt.figure(figsize=(10, 5)) plt.plot(frequencies, np.abs(spectrum) / np.max(np.abs(spectrum)), color='green', label='Спектр исходного сигнала') plt.title('Спектр исходного сигнала') plt.xlabel('Частота') plt.ylabel('Амплитуда') plt.legend() plt.grid(True) plt.show() # Визуализация отфильтрованного сигнала plt.figure(figsize=(10, 5)) plt.plot(filtered_signal, color='green', label='Отфильтрованный сигнал') plt.title('Отфильтрованный сигнал') plt.xlabel('Время') plt.ylabel('Амплитуда') plt.legend() plt.grid(True) plt.show() plt.figure(figsize=(10, 5)) plt.plot(frequencies, np.abs(filtered_spectrum) / np.max(np.abs(filtered_spectrum)), color='green', label='Спектр отфильтрованного сигнала') plt.title('Спектр отфильтрованного сигнала') plt.xlabel('Частота') plt.ylabel('Амплитуда') plt.legend() plt.grid(True) plt.show() # Спектограмма до и после фильтрации plt.figure(figsize=(12, 6)) plt.subplot(2, 1, 1) plt.specgram(signal, NFFT=1024, Fs=sampling_rate, noverlap=512, cmap='hot') plt.title('Спектограмма исходного сигнала') plt.xlabel('Время') plt.ylabel('Частота') plt.subplot(2, 1, 2) plt.specgram(filtered_signal, NFFT=1024, Fs=sampling_rate, noverlap=512, cmap='hot') plt.title('Спектограмма отфильтрованного сигнала') plt.xlabel('Время') plt.ylabel('Частота') plt.tight_layout() plt.show() # Запись отфильтрованного сигнала в файл wavfile.write('LR2MUSIC.1.wav', sampling_rate, (filtered_signal * 32767).astype(np.int16))
|
После обработки звучание стало напоминать шипение. На графиках (рис. 6-9) представлена визуализация исходного и отфильтрованного сигнала, также на рисунке 10 представлена спектрограмма.
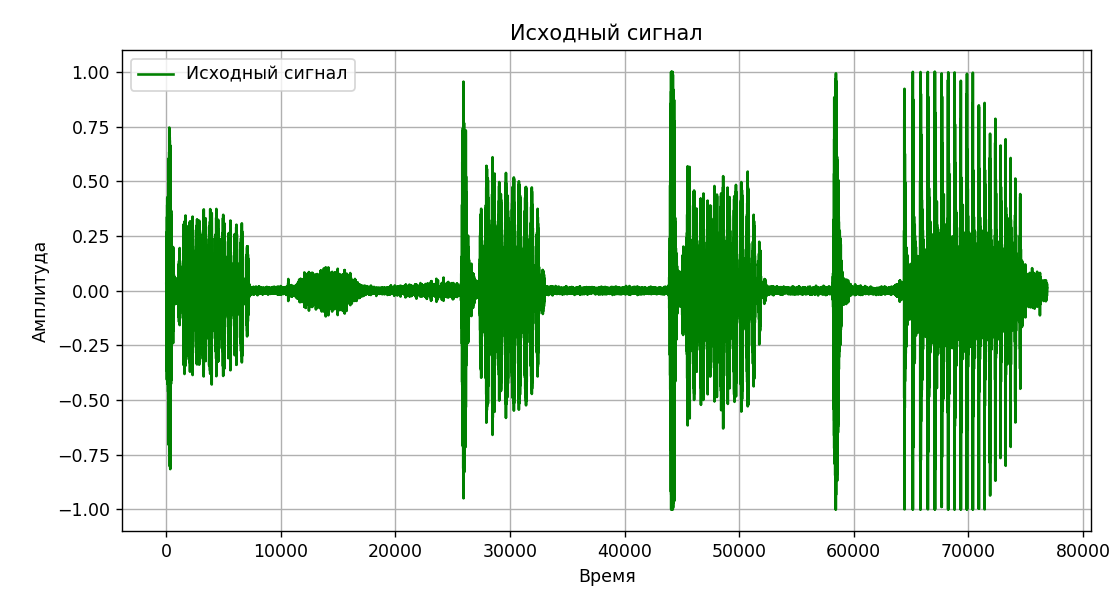
Рисунок 6 – Визуализация исходного сигнала
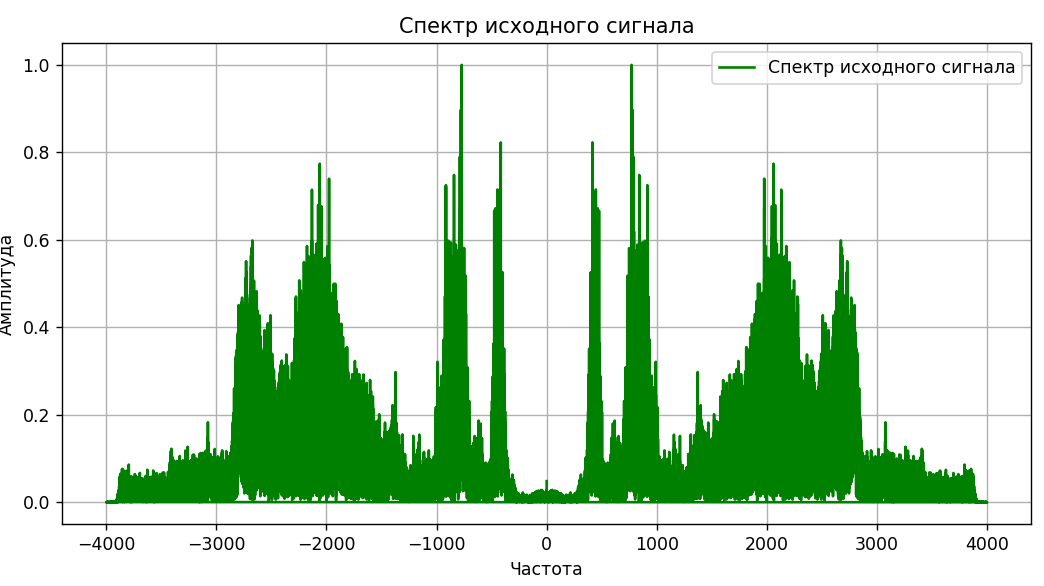
Рисунок
7 – Визуализация исходного сигнала
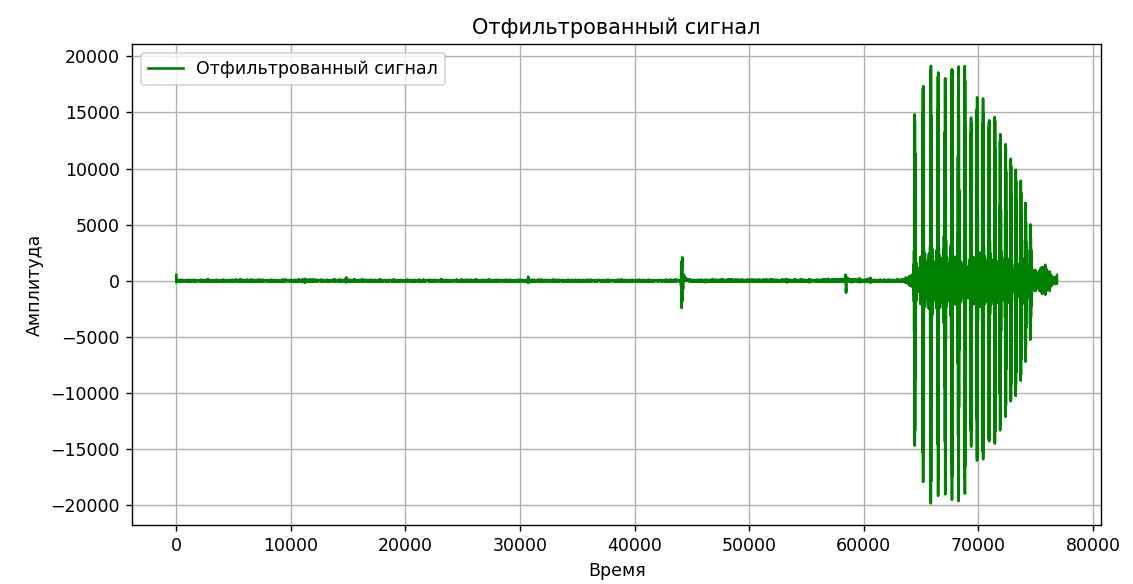
Рисунок 8 – Визуализация отфильтрованного сигнала
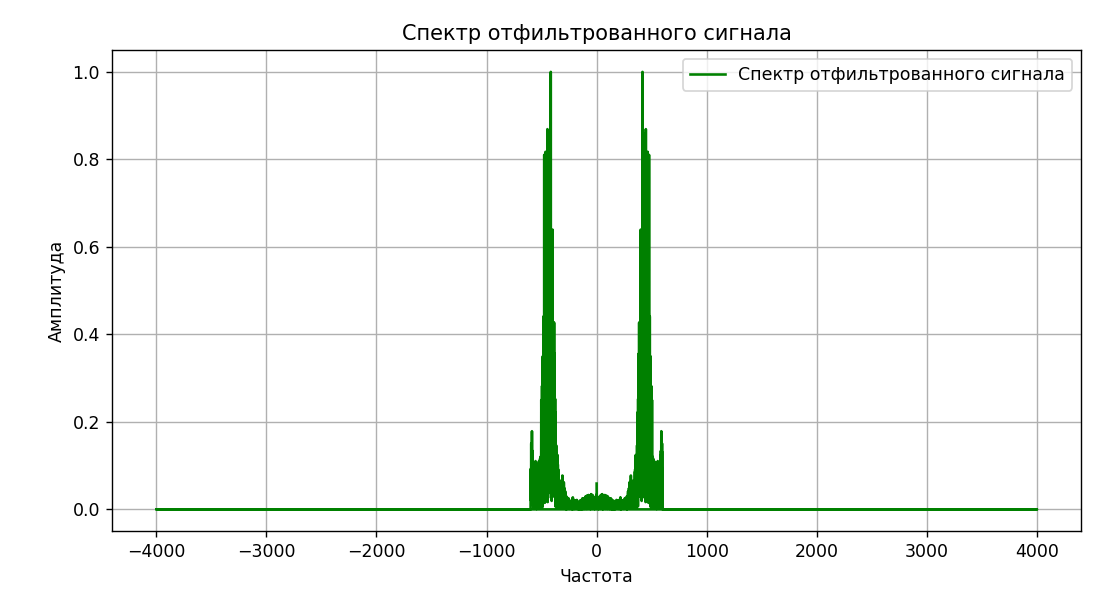
Рисунок
9 – Визуализация отфильтрованного
сигнала
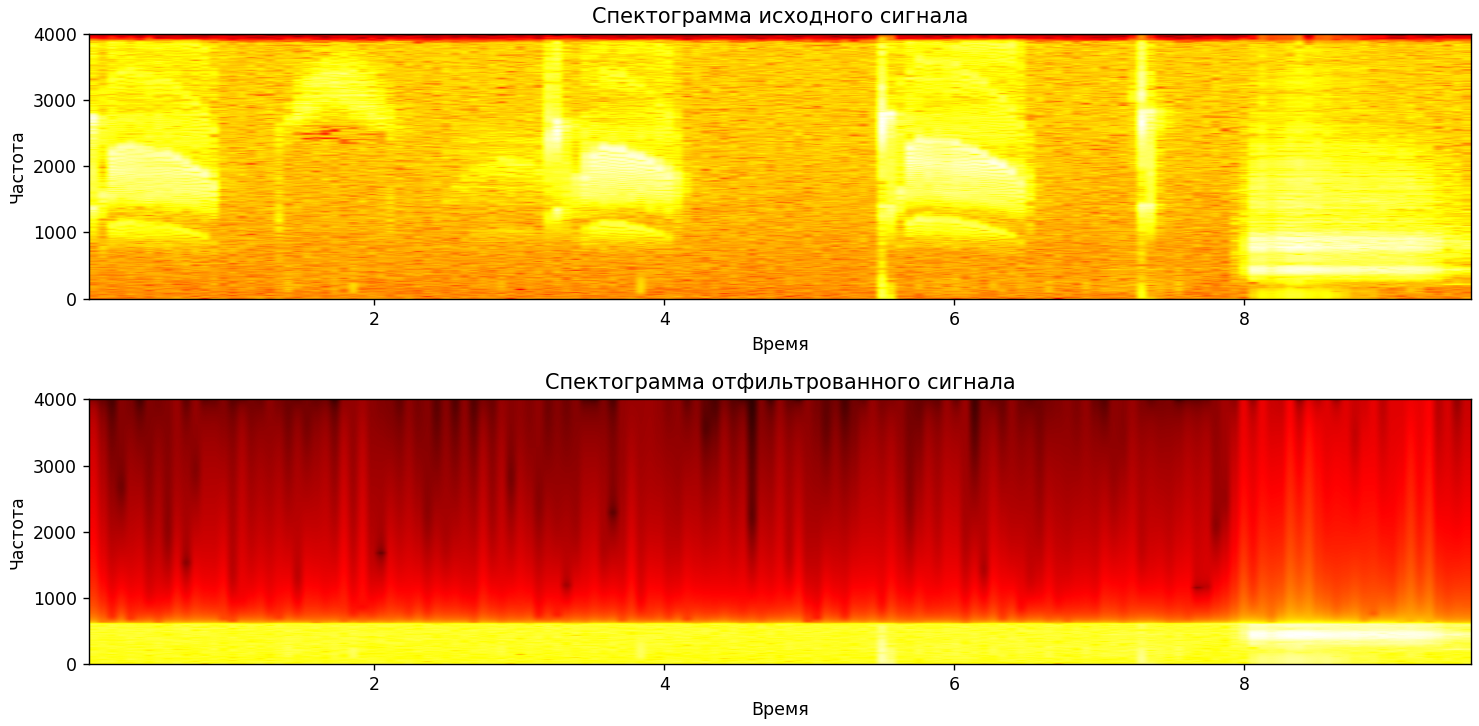
Рисунок 10 – Визуализация спектрограммы сигналов
Вывод
В ходе данной работы был реализован фильтр нижних частот, охватывающий диапазон до 1500 Гц. Входные и выходные сигналы были проанализированы как в частотной, так и во временной областях. Фильтрация значительно изменила спектр сигналов, удалив высокие частоты. В ходе эксперимента были обработаны как сгенерированные модельные сигналы, так и реальные аудиокомпозиции. Метод обработки в частотной области с использованием преобразования Фурье продемонстрировал свою эффективность при изменении спектральных характеристик сигнала. Однако итоговый звук оставляет желать лучшего и звучит ужасно, что ставит под вопрос практическое применение такого подхода в очистке аудиозаписей и удалении нежелательных шумов.
Ссылка на аудиофайлы: https://drive.google.com/drive/folders/1-T1Y_1foDcRzw5ROi7un1AuykKyI-kU1?usp=drive_link
Список используемых источников:
1. Мультимедиатехнологии в информационных системах. Представление и обработка изображений в компьютере: учеб. пособие/ Н. Н. Красильников, О. И. Красильникова. ГУАП. СПб, 2007. 132 с.
2. Жаринов О.О. Учебно-методические материалы к выполнению лабораторной работы №2 по дисциплине “Мультимедиа-технологии “. гр. Z0411. ГУАП, 2025. – 17 с. (Интернет-ресурс) // URL: https://pro.guap.ru/inside/student/tasks/67ac3ca7e6be4c224a6773800de961b9/dow nload
3. Аудиотехника. Учебник для вузов. / Ю.А. Ковалгин, Э.И. Вологдин – М.: Горячая линия-Телеком, 2013. – 742 с.
4. Алгоритм цифровой фильтрации в частотной и временной областях. // URL: http://stu.sernam.ru/book_g_rts.php?id=137
5. Фильтрация сигнала в частотной области - Цифровая обработка сигналов. // URL: http://www.cyberforum.ru/digital-signal

 ,
Гц
,
Гц ,
Гц
,
Гц