мсрр

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное автономное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

Кафедра 41

ПРЕПОДАВАТЕЛЬ

старший преподаватель				И. И. Спиндзак
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

Лабораторная работа №1

Механизмы распределения ресурсов нисходящего кадра в телекоммуникационных сетях

по курсу: Моделирование систем распределения ресурсов

СТУДЕНТКА ГР. №		Z0411		04.04.25		М. В. Карелина
	номер группы			подпись, дата		инициалы, фамилия

Номер студенческого билета: 2020/3477

Санкт-Петербург

2025

Цель работы:

Получение навыков моделирования стандартных сценариев работы телекоммуникационных систем с топологией типа «звезда». Изучение свойств алгоритмов планирования ресурсов нисходящего кадра в подобных системах.

Вариант №9.

№	Модель распространения	R, м	PTX, Вт	f0, МГц	, МГц	kn
7	Окумура-Хата, large city	1,5 (км)	160	1800	20	2

Определим высоту передатчика как 50м, а высоту абонента 1.7м.

Количество абонентов в сети меняется от 2⁰ до 2⁶, то есть от 1 до 64.

Расчет уровня потерь в канале связи в разах:

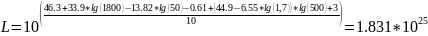
Расчет мощности сигнала, принятой АБ:

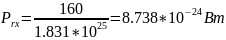
Расчет отношения сигнал/шум:

Расчет пропускную способность канала связи:

Анализируемые алгоритмы распределения ресурсов:

- Equal Blind

Этот алгоритм дает равные скорости между всеми абонентами. Доля ресурса времени, выделяемая каждому абоненту:

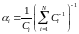
Скорость для абонента i может быть выражена как:

-Maximum Throughput:

Это алгоритм с целью максимизации пропускной способности сети:

- Proportion Fair:

Этот алгоритм выделяет равные ресурсы всем абонентам:

Суммарная скорость:

На Рисунке 1 представлено распределение 64 абонентов вокруг базовой станции.

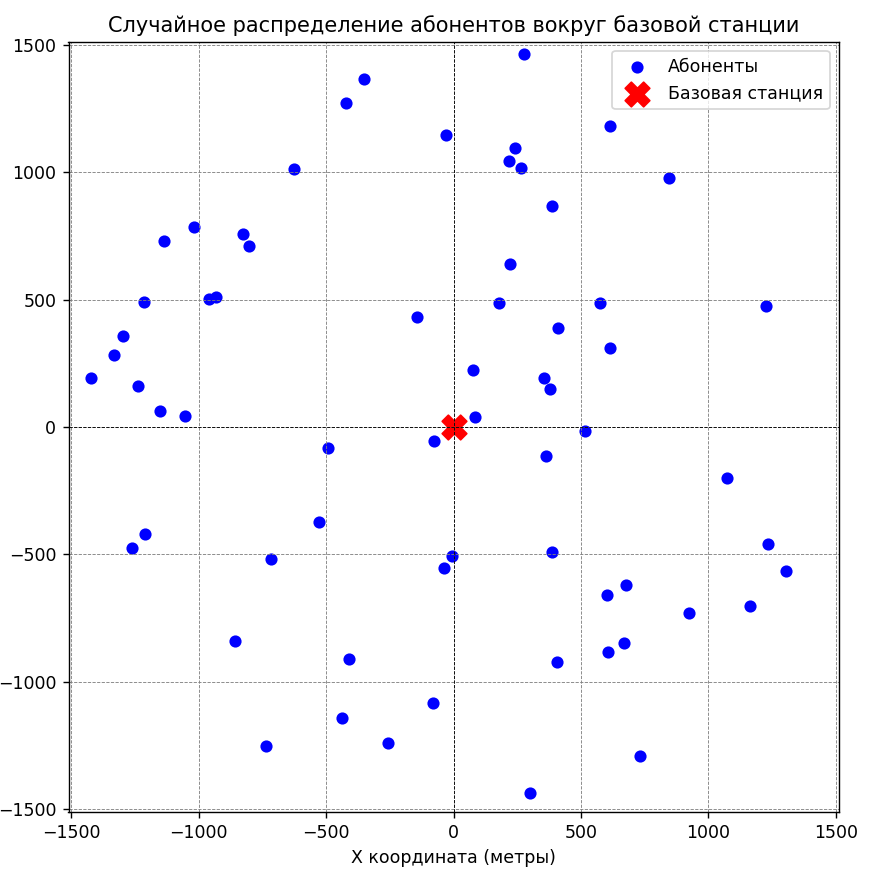
Рисунок 1 - Случайное распределение 64 абонентов вокруг базовой станции

Результаты моделирования:

Далее алгоритм 1, алгоритм 2, алгоритм 3 означают соответственно алгоритмы Equal Blind, Maximum Throughput, Proportion Fair.

На графике, отображающем оценку суммарной скорости, видно, что алгоритм Maximum Throughput демонстрирует рост при увеличении числа абонентов. Это связано с тем, что с ростом числа пользователей в сети возрастает вероятность нахождения абонента вблизи базовой станции. В то же время остальные алгоритмы не показывают значительных изменений в пропускной способности при увеличении выборки. Согласно формуле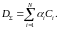 и формулам наших алгоритмов, в первом случае мы распределяем одинаковые скорости между абонентами, а во втором — предоставляем равные доли, что приводит к схожей динамике поведения алгоритмов 1 и 2.

Рисунок 2 - Оценка суммарной скорости

Из графика, иллюстрирующего оценку средней скорости, следует, что при увеличении размера выборки, то есть числа абонентов, пропускная способность стремится к определённому значению, что снижает погрешность вычислений.

Рисунок 3 - Оценка средней скорости

График оценки минимальной скорости демонстрирует схожее поведение для алгоритмов 1 и 2. Однако для второго алгоритма ситуация иная, поскольку в алгоритме Maximum Throughput мы выделяем максимальную скорость одному абоненту. Соответственно, при наличии более одного абонента минимальная скорость будет равна 0.

Рисунок 4 - Оценка минимальной скорости

Программа включает три функции. В первой функции, random_user, происходит генерация случайных пользователей. На вход подается количество пользователей, а на выходе получаются расстояние до базовой станции и координаты x и y для построения графика. Во второй функции, kanal, вычисляется пропускная способность канала связи; на вход подается количество пользователей, а на выходе — значение пропускной способности. В последней функции, rate, рассчитывается средняя оценка для трех алгоритмов. Код программы приведен в Листинге 1.

Листинг 1. Код программы для моделирования распределения ресурсов

import numpy as np import matplotlib.pyplot as plt R = 1.5 Ptx = 160 F0 = 1800 DF = 3 * 10**6 KN = 20 K = 1.38 * 10**(-23) Hbs = 50 Hrx = 1.7 S = 3 # маленький город T = 300 def random_user(N): # Генерация случайных величин, равномерно распределенных на радиусе length = np.sqrt(np.random.uniform(0, R ** 2, N)) angle = np.random.uniform(0, 2 * np.pi, N) x = length * np.cos(angle) y = length * np.sin(angle) return length, x, y # Рассчет пропускной способности канала связи def kanal(N): length, x, y = random_user(N) Pn = DF * T * K * KN # мощность шума Ah = (1.1 * np.log10(F0) - 0.7) * Hrx - (1.56 * np.log10(F0) - 0.8) # Модель Окамура–Хаты L = 10 ** ((46.3 + 33.9 * np.log10(F0) - 13.82 * np.log10(Hbs) - Ah + (44.9 - 6.55 * np.log10(Hrx)) * np.log10(length) + S) / 10) Prx = Ptx / L # расчёт мощности SNR = Prx / Pn # сигнал/шум C = DF * np.log2(1 + SNR) # макс пропускная способность канала связи return C def rate(): # Расчет оценки MOsum1total, MOmean1total, MOmin1total = [], [], [] # Алгоритм 1 Dsum, Dср, Dмин MOsum2total, MOmean2total, MOmin2total = [], [], [] MOsum3total, MOmean3total, MOmin3total = [], [], [] # Перебор значений N, начиная с 1, 2, 4, 8,..., 64 lenN = [2 ** i for i in range(7)] # Начиная с 1, заканчивая 64 for N in lenN: MOsum1, MOmean1, MOmin1 = [], [], [] MOsum2, MOmean2, MOmin2 = [], [], [] MOsum3, MOmean3, MOmin3 = [], [], [] for q in range(100): # Повторение эксперимента 100 раз Ci = kanal(N) eb = [(1 / np.sum(Ci**(-1))) for i in Ci] mt = [np.max(Ci)] + [0 for i in range(N - 1)] pf = [i / N for i in Ci] # 1 алгоритм MOsum1.append(np.sum(eb)) MOmean1.append(np.mean(eb)) MOmin1.append(np.min(eb)) # 2 алгоритм MOsum2.append(np.sum(mt)) MOmean2.append(np.mean(mt)) MOmin2.append(np.min(mt)) # 3 алгоритм MOsum3.append(np.sum(pf)) MOmean3.append(np.mean(pf)) MOmin3.append(np.min(pf)) MOsum1total.append(np.mean(MOsum1)) MOmean1total.append(np.mean(MOmean1)) MOmin1total.append(np.mean(MOmin1)) MOsum2total.append(np.mean(MOsum2)) MOmean2total.append(np.mean(MOmean2)) MOmin2total.append(np.mean(min(MOmin2))) # !!!!!!!!! MOsum3total.append(np.mean(MOsum3)) MOmean3total.append(np.mean(MOmean3)) MOmin3total.append(np.mean(MOmin3)) plt.plot(lenN, MOsum1total, label='Алгоритм 1') plt.plot(lenN, MOsum2total, label='Алгоритм 2') plt.plot(lenN, MOsum3total, label='Алгоритм 3') plt.xlabel('Кол. абонентов') plt.ylabel('Пропускная способность бит/с') plt.legend() plt.title('Оценка сумм. скорости') plt.show() plt.plot(lenN, MOmean1total, label='Алгоритм 1') plt.plot(lenN, MOmean2total, label='Алгоритм 2') plt.plot(lenN, MOmean3total, label='Алгоритм 3') plt.xlabel('Кол. абонентов') plt.ylabel('Пропускная способность бит/с') plt.legend() plt.title('Оценка сред. скорости') plt.show() MOmin2total[0] = MOmin1total[0] plt.plot(lenN, MOmin1total, label='Алгоритм 1') plt.plot(lenN, MOmin2total, label='Алгоритм 2') plt.plot(lenN, MOmin3total, label='Алгоритм 3') plt.xlabel('Кол. абонентов') plt.ylabel('Пропускная способность бит/с') plt.legend() plt.title('Оценка мин. скорости') plt.show() rate()

Вывод

В результате анализа полученных графиков можно сделать несколько выводов относительно трех представленных алгоритмов. Алгоритм Maximum Throughput демонстрирует наибольшую эффективность в ситуациях, когда абоненту нужно быстро скачать небольшой файл. В таких случаях он обеспечивает максимальную скорость передачи данных, что значительно сокращает время загрузки. Тем не менее, его использование может быть не самым оптимальным решением, если абоненты находятся на различных расстояниях от базовой станции, поскольку он не учитывает эти расстояния при распределении ресурсов.

Алгоритм Equal Blind оптимально подходит для сценариев, когда абоненты расположены примерно на одинаковом расстоянии от базовой станции. В этом случае он обеспечивает более равномерное распределение пропускной способности. Однако, если абоненты распределены неравномерно — например, некоторые находятся далеко от базовой станции — это требует значительного снижения скорости передачи данных для пользователей, находящихся ближе, чтобы предоставить больше ресурсов тем, кто находится дальше. Такой подход не всегда может быть оптимальным, так как его эффективность сильно зависит от размещения пользователей.

Алгоритм Proportionally Fair предлагает более сбалансированное распределение ресурсов среди пользователей, особенно когда они находятся на разных расстояниях от базовой станции. Он обеспечивает более высокую среднюю скорость, чем алгоритм Equal Blind, и может считаться предпочтительным в большинстве случаев, поскольку более справедливо распределяет пропускную способность на основе пропорционального подхода.

При сравнении алгоритмов Proportionally Fair и Maximum Throughput можно выявить небольшую разницу в средней и минимальной скорости, составляющую около 3%-6% (или 0.05-0.2 Мбит/с), что указывает на определенное преимущество алгоритма Proportionally Fair в контексте обеспечения более справедливого распределения ресурсов между абонентами. Этот алгоритм гарантирует более стабильную и надежную работу системы, способствуя равномерному распределению пропускной способности даже при наличии различных расстояний пользователей от базовой станции.