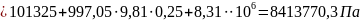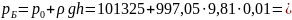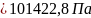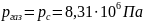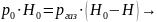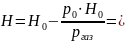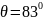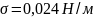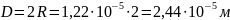ФИО	Группа	Дата	Вариант
Чижова Анастасия Васильевна	2Д12	20.02.2025	24

Практическое задание № 1. Дисциплина «Макрокинетика химических процессов». Тема «Капиллярные явления»

А) Рассчитать давление p_А в пузырьке газа, защемленном водой в цилиндрическом капилляре радиуса R₀ [1]. Условия: окружающее давление p₀ = 1 атм, температура Т = 298 К, угол смачивания θ = 30°, положение мениска задано значением H_А. Поверхностное натяжение воды принять равным σ = 0,072 Н/м. Плотность найти по любому подходящему справочнику, ссылку на справочник указать.

Б) Аналогично, рассчитать давление p_Б в пузырьке газа, защемленном водой в цилиндрическом капилляре радиуса R₀, если горло капилляра находится на одном уровне с уровнем воды в сосуде (Н_Б ≈ 0). В ситуации Б мениски одинаковы, h = 10 мм. Остальные исходные данные такие же.

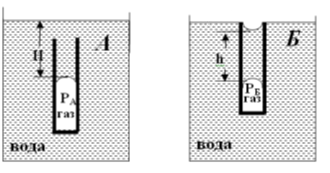
Рисунок — Модели капилляров

Таблица — Варианты заданий

№ варианта	Радиус капилляра R0, нм	НА, см
4	15	25

Ход решения и основные расчетные формулы [2]:

Давление под искривленной поверхностью жидкости p_ж и давление в газе над жидкостью р_г связаны между собой следующим выражением: р_с = ± (p_ж – р_г), где р_с — т.н. капиллярное давление (лапласово давление).

Т.к. в ситуациях А и Б вода ведет себя как частично смачивающая жидкость (0 < θ < 90°), наблюдается вогнутая поверхность мениска, причем давление будет выше там, где находится центр искривленной поверхности. Значит для всех рассматриваемых менисков р_с = – (p_ж – р_г) = р_г – p_ж.

Согласно закону Лапласа:

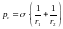
где r₁ и r₂ — главные радиусы кривизны искривленной поверхности; σ — поверхностное натяжение, Н/м.

Для сферического мениска с радиусом кривизны r: .

Для ситуаций А и Б 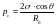. Угол смачивания (краевой угол) θ отсчитывается внутри жидкости.

Для ситуации А: давление p_А в пузырьке газа равно p_А = p₀ + ρgH + р_с.

Для ситуации Б:

— гидростатическое давление в жидкости под верхним мениском равно (p₀ – р_с);

— гидростатическое давление в жидкости над нижним мениском равно (p₀ – р_с + ρgh);

— гидростатическое давление в пузырьке газа под нижним мениском равно p_Б = p₀ – р_с + ρgh + р_с = p₀ + ρgh.

Решение:

А)

Дано: р0 = 1 атм = 101325 Па Т = 298 К HA = 25 см = 0,25 м	Решение: Капиллярное давление : Давление в пузырьке газа : Плотность воды при 298 К из [5].
Найти: рА - ?	Ответ:

Б)

Дано: р0 = 1 атм = 101325 Па Т = 298 К h = 10 мм = 0,01 м	Решение: Давление в пузырьке газа: Плотность воды при 298 К из [5].
Найти: рБ - ?	Ответ:

2. Определить высоту поднятия воды Н в вертикально погруженном в воду и опрокинутом вверх дном тонком цилиндрическом капилляре радиусом R и высотой Н₀. Первоначально капилляр был полностью заполнен воздухом при давлении р₀ = 1 атм.

Высота Н₁ = 0,15 м; угол смачивания θ = 30°; поверхностное натяжение воды σ = 0,072 Н/м.

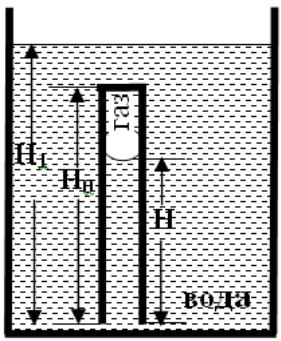
Рисунок — Модель капилляра

Таблица — Варианты заданий

№ варианта	Радиус капилляра R, нм	Полная высота капилляра Н0, см
4	15	8

Ход решения и основные расчетные формулы:

Заполнение капилляра водой обусловлено капиллярным давлением .

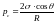В незаполненной жидкостью части капилляра происходит сжатие газа, определяемое соотношением для идеальных газов: p₀ · H₀ = p_газ · (H₀ – H), где p_газ — давление защемленного газа.

В условиях равновесия p_газ = p_c + ρg(H₁ – H), причем для капилляров с нанометровыми радиусами p_c >> ρg(H₁ – H).

Решение:

Дано: H0 = 8 см = 0,08 м р0 = 1 атм = 101325 Па H1 = 0,15 м	Решение: Капиллярное давление : Если pc >> ρg(H1 – H), тогда гидростатическим давлением пренебрегаем. Давление защемленного газа в условии равновесия ргаз: Высота поднятия воды Н:
Найти: Н - ?	Ответ: Н = 0,079 м

3. Определить наибольший диаметр пор в фитиле керосиновой горелки, обеспечивающий подъем керосина от дна до горелки на высоту H. Считать поры цилиндрическими трубками постоянного сечения, угол смачивания θ = 83°, поверхностное натяжение керосина σ = 0,024 Н/м.

Таблица — Варианты заданий

№ варианта	Высота фитиля, см	Плотность керосина, г/см3
4	6	0,810

Ход решения и основные расчетные формулы:

Высота поднятия H определяется балансом между капиллярными силами и силами тяжести:

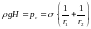
Для цилиндрического капилляра радиусом R наблюдается сферический мениск:

Решение:

Дано: Н = 6 см = 0,06 м	Решение:
Найти: D - ?	Ответ:

4. Давление насыщенного пара азота над плоской поверхностью жидкого азота в интервале температур 60,81–83,65 К удовлетворительно описывается уравнением:

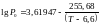
где P₀ — давление насыщенного пара азота, бар (1 бар = 10⁵ Па); Т — температура, К.

Рассчитайте давление насыщенных паров азота над искривленной поверхностью жидкого азота, заключенного в порах пористого материала, при температурах 61–83 К с шагом 1 К. Принять, что поры образованы двумя плоскопараллельными пластинами. Расстояние между пластинами приведено в таблице с исходными данными.

Жидкий азот хорошо смачивает поверхность твердого тела, cos θ ≈ 1 [3]. Примите плотность жидкого азота на всем интервале температур 0,8043 г/см³, поверхностное натяжение — 8,72 мДж/м².

Примите расстояние между пластинами, выраженное в нанометрах, численно равным номеру вашего варианта.
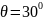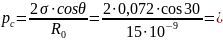
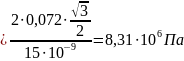