индивидуальные работы / индивидуальная работа 2 / индивидуальная работа моделирование экономических процессов вариант 2 часть 3

МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РФ

ФГБОУ ВО «Пензенский ГАУ»

Кафедра «Финансы и информатизация бизнеса»

ИНДИВИДУАЛЬНАЯ РАБОТА №1

по дисциплине: «Моделирование экономических процессов»

Вариант 2

Пенза, 2024

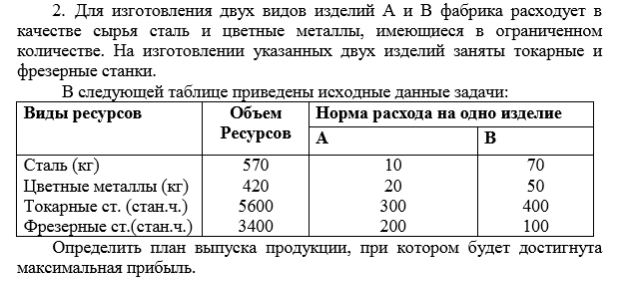
Определить план выпуска, при котором будет произведено максимальное количество изделий.

Решение:

Обозначим за переменные х1, х2 – количество изделий А, В соответственно. Составим систему ограничений:

1. по стали: 10*х1+70*х2 ≤ 570

2. по цветным материалам: 20*х1+50*х2 ≤ 420

3. по токарным станкам: 300*х1+400*х2 ≤ 5600

4. по фрезерным станкам: 200*х1+100*х2 ≤ 3400

Так как критерий оптимальности – максимально количество изготовленных изделий, то целевая функция примет вид:

Z = х1+х2 → max

Условие неотрицательности переменных: х1 ≥ 0; х2 ≥ 0; х3 ≥ 0.

После составления системы ограничений вносим данные в матрицу в Excel (рис.1).

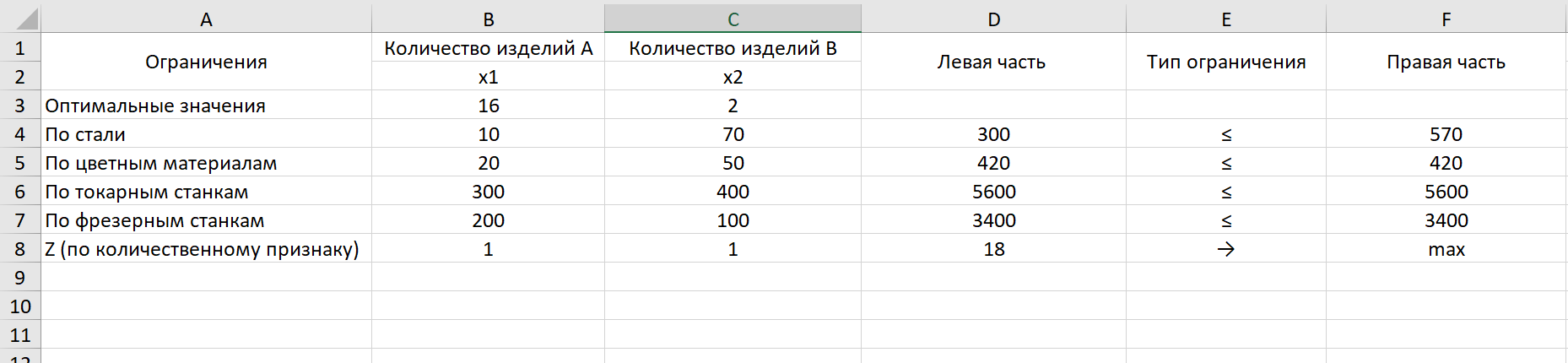
Рис. 1 – Внесение данных в матрицу в Excel

Воспользуемся встроенной функцией СУММПРОИЗВ и найдем столбец «Левая часть». Для этого в соответствующие массивы вносим данные по ограничениям. Важно чтобы в столбце ячейки имели значение, равное нулю. (рис.2).

Рис. 2 – Нахождение столбца «Левая часть»

Выбираем клетку D7 и заполняем диалоговое окно «Параметры поиска решений» (рис.3).

Рис. 3 – Диалоговое окно «Параметры поиска решений»

Добавляем каждое из ограничений и выбираем метод решения – симплекс-методом (рис. 4 и рис. 5).

Рис. 4 – Добавление ограничений

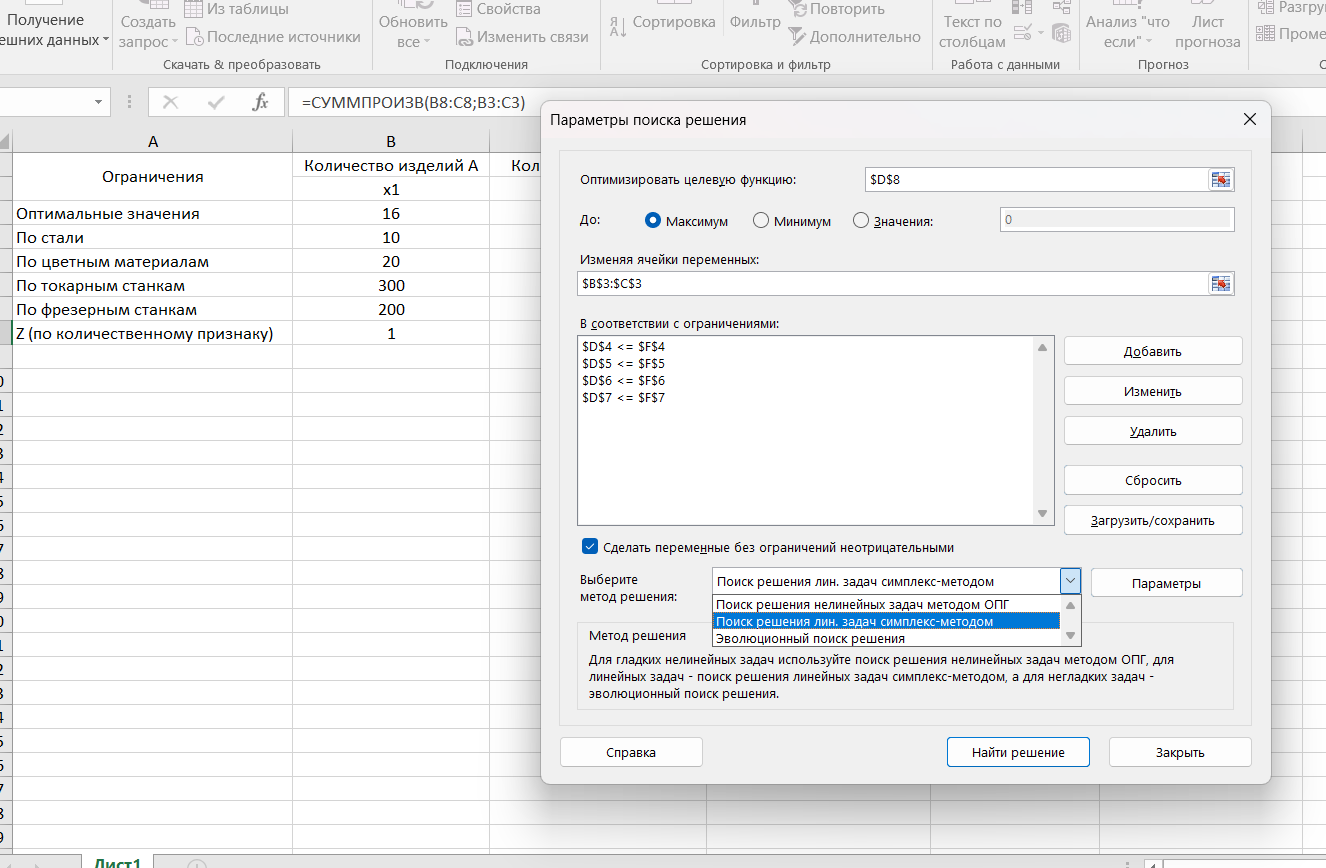
Рис. 5 – Поиск решения симплекс-методом

После нахождения решения появляется диалоговое окно «Результаты поиска решения» (рис.6).

Рис. 6 – Диалоговое окно «Результаты поиска решения»

В результате после выполнения всех необходимых операций мы получаем заполненную матрицу (рис.7).

Рис. 7 – Итоговая матрица

Анализируя оптимальное решение, можно сделать вывод, что целесообразно будет производить продукцию А и В в количестве 12 и 3 единиц соответственно, производство продукции С является нецелесообразным. Прибыль при этом составит 54 дол. Время работы на III устройстве является лимитирующим.