индивидуальные работы / индивидуальная работа 2 / индивидуальная работа моделирование экономических процессов вариант 2 часть 1

МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РФ

ФГБОУ ВО «Пензенский ГАУ»

Кафедра «Финансы и информатизация бизнеса»

ИНДИВИДУАЛЬНАЯ РАБОТА №2

по дисциплине: «Моделирование экономических процессов»

Вариант 2

Пенза, 2024

РЕШЕНИЕ

Построим экономико-математическую модель задачи. Обозначим за переменные участки, пригодные для трансформации угодий из i-ых севооборотов в j-ые участки (рис.1).

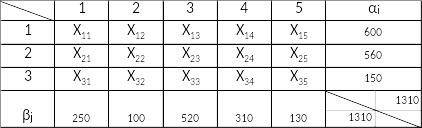
Рис.1 - Экономико-математическая модель

Из рисунка 1 видно, что соблюдается равенство:

Следовательно, задача является закрытого типа.

Составим ограничения. Первая группа ограничений по севообороту:

1. X₁₁ + X₁₂ + X₁₃ + X₁₄ + X₁₅ = 600

2. X₂₁ + X₂₂ + X₂₃ + X₂₄ + X₂₅ = 560

3. X₃₁ + X₃₂ + X₃₃ + X₃₄ + X₃₅ = 150

Вторая группа ограничений по видам участков:

4. X₁₁ + X₂₁ + X₃₁ = 250

5. X₁₂ + X₂₂ + X₃₂ = 100

6. X₁₃ + X₂₃ + X₃₃ = 520

7. X₁₄ + X₂₄ + X₃₄ = 310

8. X₁₅ + X₂₅ + X₃₅ = 130

Так как критерий оптимальности – чистый доход при размещении на данном участке, то целевая функция примет вид:

Z=800X₁₁+1100X₁₂+800X₁₃+600X₂₄+440X₁₅+1000X₂₁+1800X₂₂+2000X₂₃+2200X₂₄+2000X₂₅+550X₃₁+440X₃₂+380X₃₃+300X₃₄+700X₃₅.

МЕТОД НАИБОЛЬШЕГО ЭЛЕМЕНТА

Суть этого метода – на каждом шаге алгоритма поиска опорного решения стараться занять максимально возможным ресурсом прежде всего клетки, в которых лежат наибольшее значение Cij (рис.2).

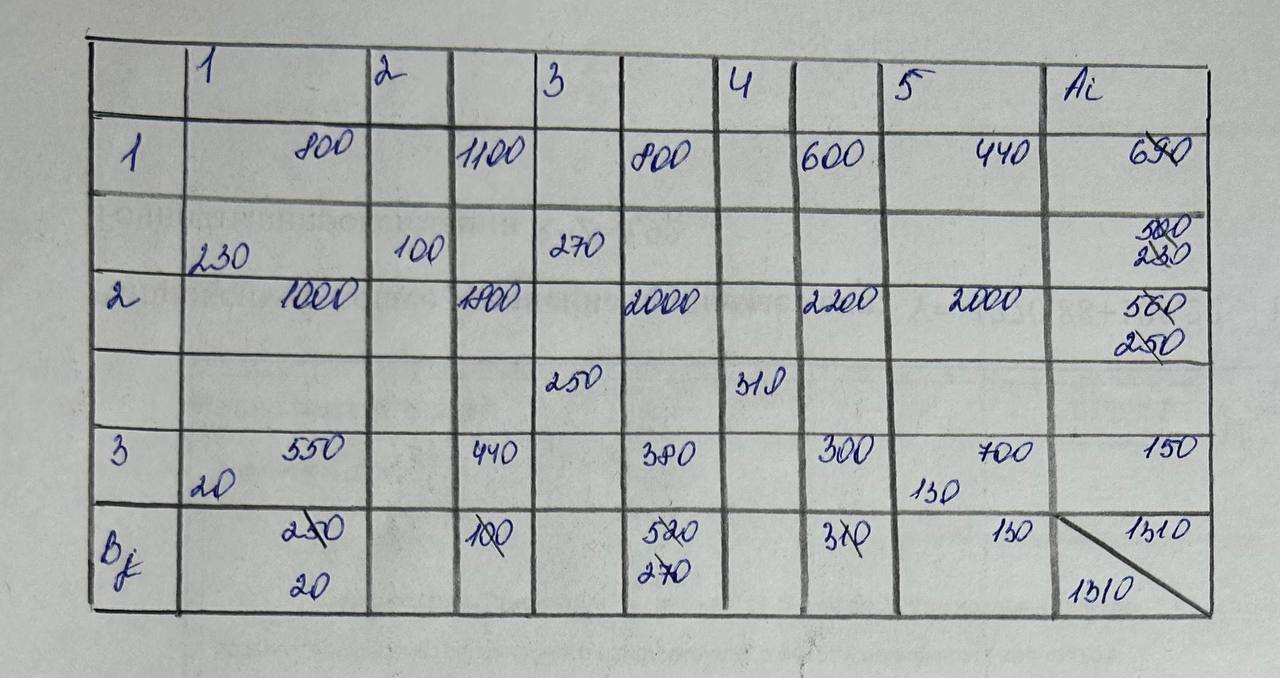
Рис.2 – Метод наибольшего элемента

При использовании метода наибольшего элемента было получено следующее опорное решение: X₁₁ =230, X₁₂=100, X₁₃ =270, X₂₃=250, X₂₄=310, X₃₁=20, X₃₅=130.

Найдем значение целевой функции:

Z=230*800+100*1100+270*800+250*2000+310*2200+20*550+130*700=1794000

Проверим решение по количеству занятых клеток:

Кзан = 7; (m+n-1) = (3+5-1) = 7 → Кзан <(m+n-1) → решение базисное, невырожденное.

МЕТОД ФОГЕЛЯ

Суть метода заключается в том, что на каждом шаге выбор очередной клетки, заполняемой ресурсом, осуществляется не на основании оценки строго локальных оценок стоимостей Cij, а на основе расчетов штрафов, позволяющих приближенно оценивать полезность данного шага с точки зрения скорейшего приближения к оптимальному решению с учетом состояния таблицы на следующем шаге (рис.3).

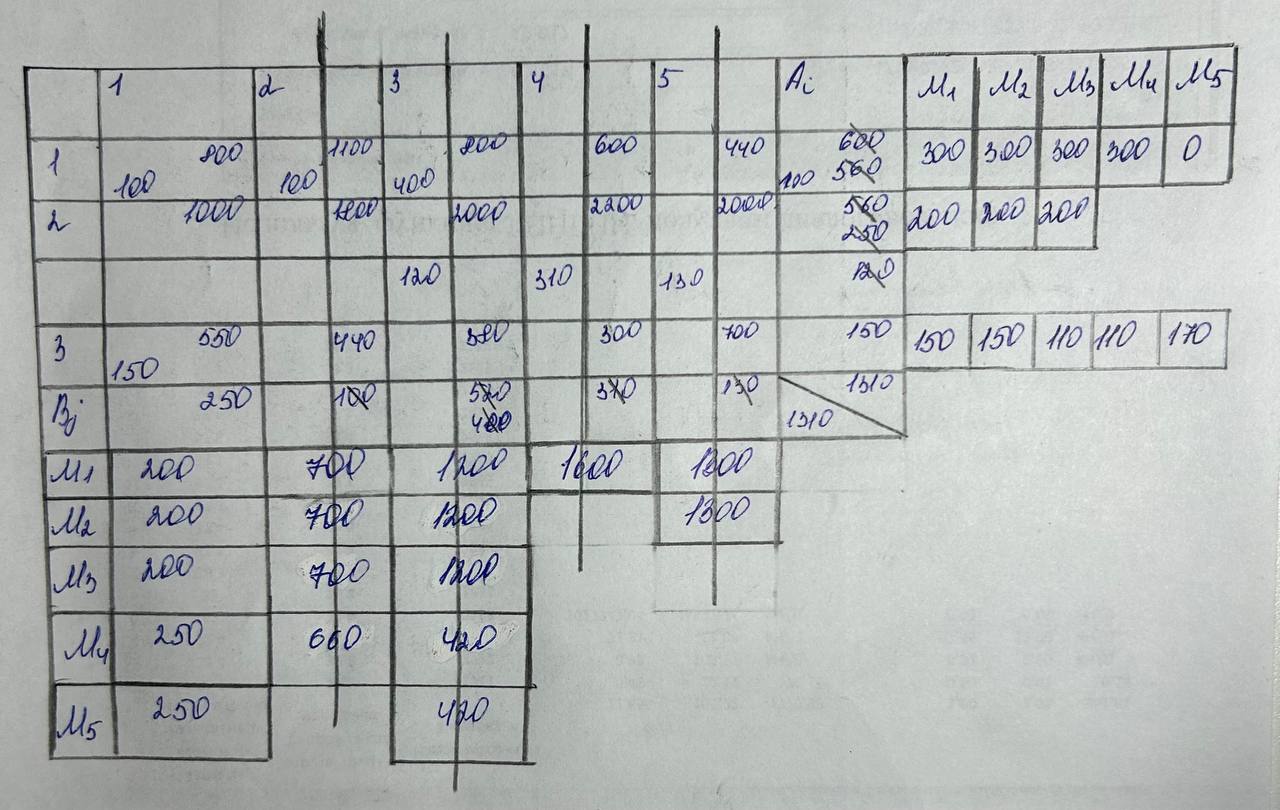
Рис.3 – Методом Фогеля

При использовании метода Фогеля было получено следующее опорное решение: X₁₁ =100, X₁₂ =100, X₁₃=400, X₂₃=120, X₂₄=310, X₂₅=130, X₃₁ =150,.

Найдем значение целевой функции:

Z=100*1100+100*800+400*800+120*2000+310*2200+130*2000+150*550=1774500

Так же, как и в методе наибольшего элемента, проверим решение по количеству занятых клеток:

Кзан = 7; (m+n-1) = (3+5-1) = 7

Кзан <(m+n-1) → решение базисное, невырожденное.

МЕТОД ПОТЕНЦИАЛОВ

Сделаем проверку решения, полученного методом наибольшего элемента, на оптимальность (рис.4).

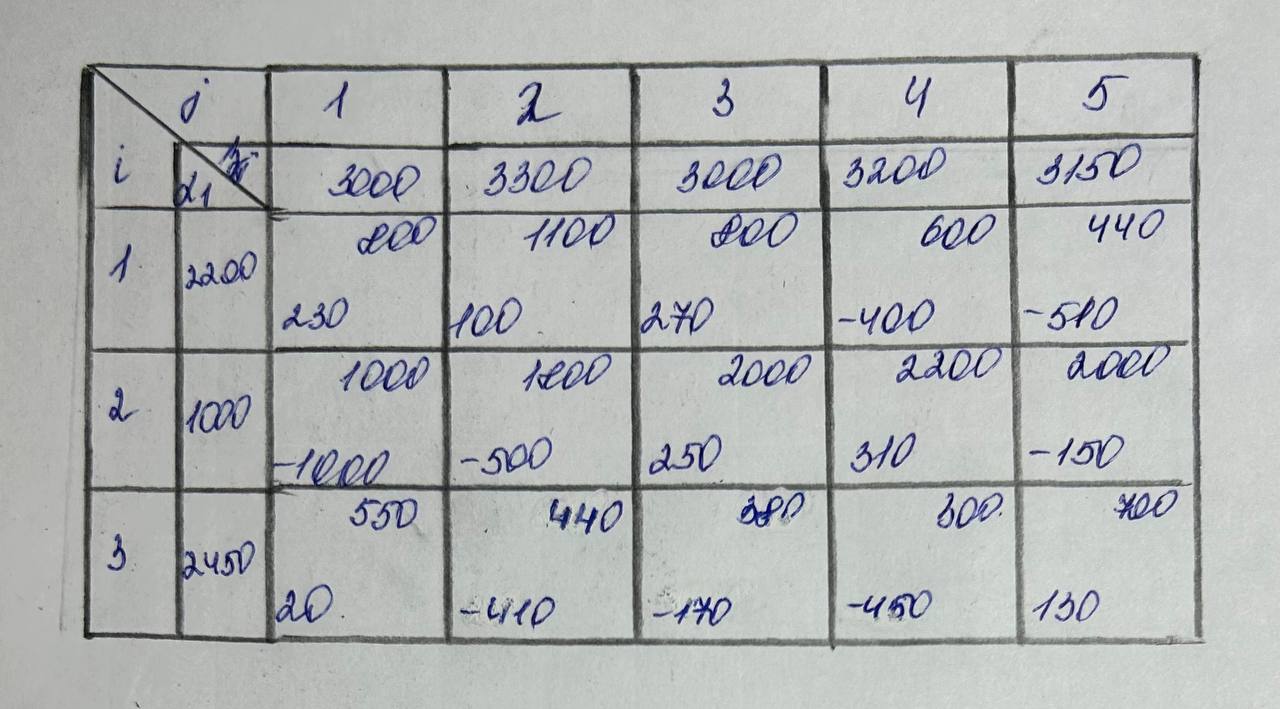
Рис.4 – Проверка методом потенциалов

В случаи максимизации целевой функции решение оптимально, если все оценки незанятых клеток удовлетворяют условию неположительности.

Так как все оценки незанятых клеток имеют отрицательные значения, делаем вывод об оптимальности решения, полученного методом наибольшего элемента.

РЕШЕНИЕ ЗАДАЧИ В ПП MS EXCEL

Если сравнить значения целевых функций в опорных планах, полученных методом наибольшего элемента и методом Фогеля, можно увидеть, что большее из них соответствует методу наибольшего значения и равен 1808000.

Сделаем проверку, решив задачу в ПП MS Excel.

Для начала заполняем две таблицы: «Матрица стоимости» и «Матрица распределения участков»» (рис.5).

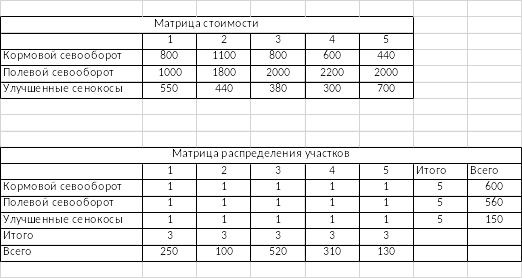
Рис.5 - Матрица стоимости и Матрица распределения участков

Далее заполняем «Расчетную матрицу». Для этого копируем «Матрицу распределения участков», не захватывая строку и столбец Всего. В каждой ячейке удаляем единицу и находим значение, умножая кормовой севооборот из «Матрицы стоимости»» на кормовой севооборот из Матрицы распределения участков» (рис.6).

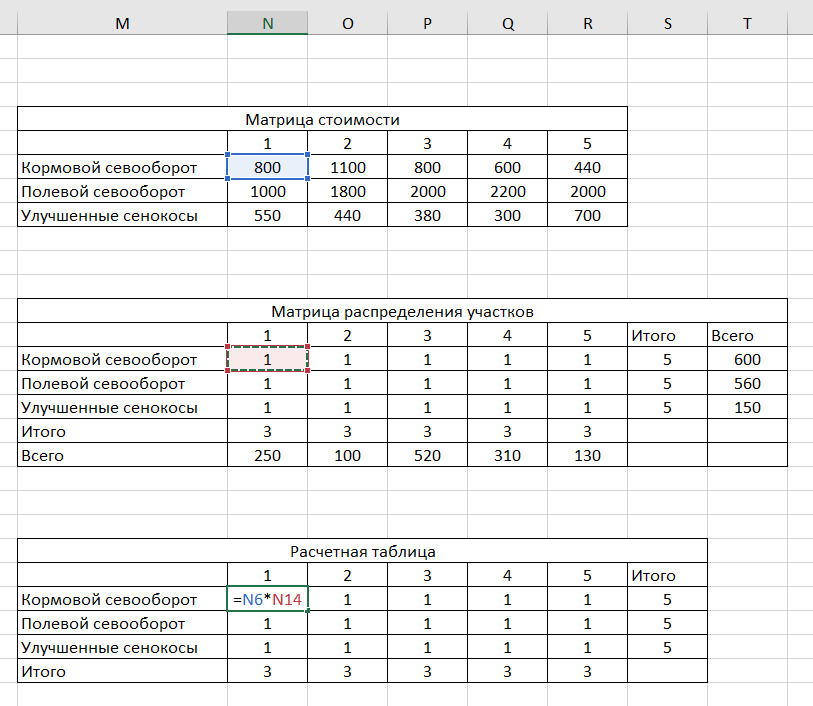
Рис. 6 – Расчет «Расчетной матрицы»

Для того, чтобы найти оптимальное решение, выделяем ячейку S27 и заполняем диалоговое окно «Параметры поиска решений» (рис.7).

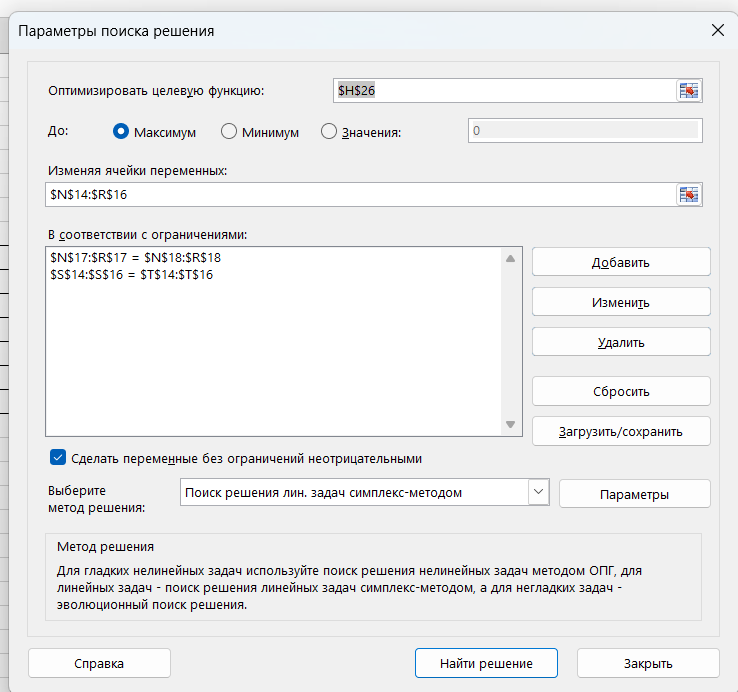
Рис.7 - Диалоговое окно «Параметры поиска решений»

После нахождения решения появляется диалоговое окно «Результаты поиска решения» и мы получаем ответ (рис.8).

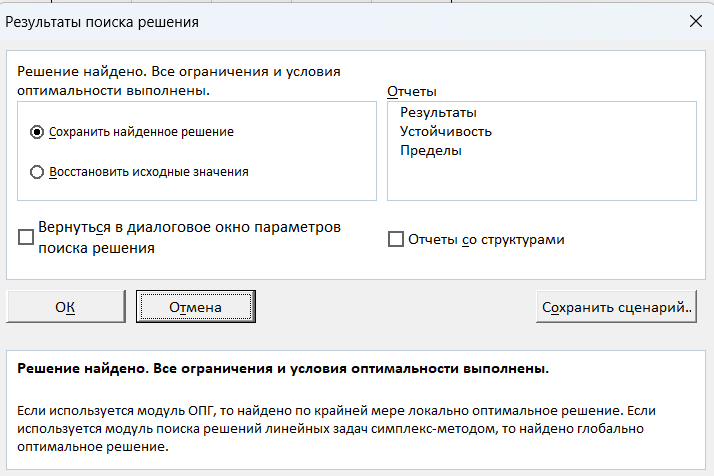
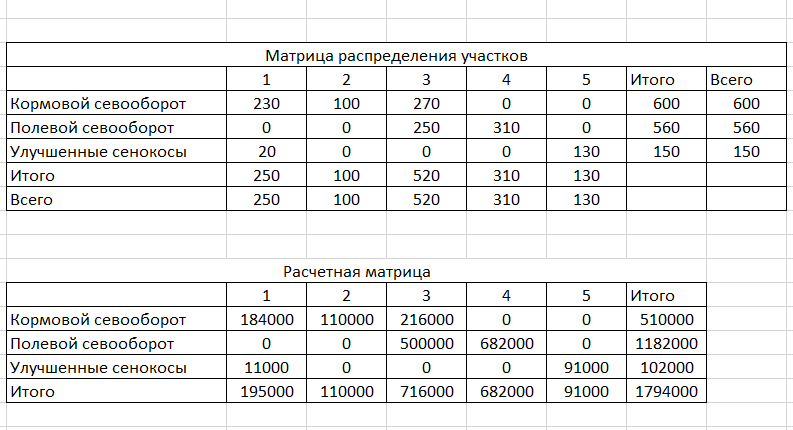
Рис. 8 - Полученный результат

Согласно полученным данным, оптимум составил 1794000. Такое же значение мы получили с помощью метода наибольшего элемента.

Оптимальное решение примет вид:

230Х₁₁+100Х₁₂+270Х₁₃+250Х₂₃+310Х₂₄+20Х₃₁+130Х₃₅ =1794000