индивидуальные работы / индивидуальная работа 1 / индивидуальная работа моделирование экономических процессов часть 2

МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РФ

ФГБОУ ВО «Пензенский ГАУ»

Кафедра «Финансы и информатизация бизнеса»

ИНДИВИДУАЛЬНАЯ РАБОТА №2

по дисциплине: «Моделирование экономических процессов»

Вариант 1

Пенза, 2024

РЕШЕНИЕ

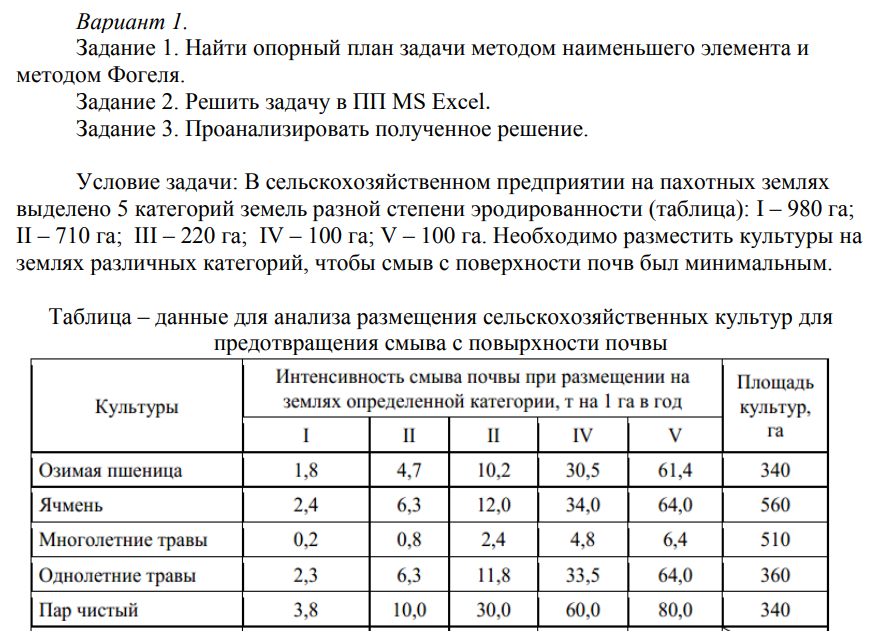
Построим экономико-математическую модель задачи. Обозначим за переменные земли разной степени эродированности из i-ых культур в j-земли. (рис.1).

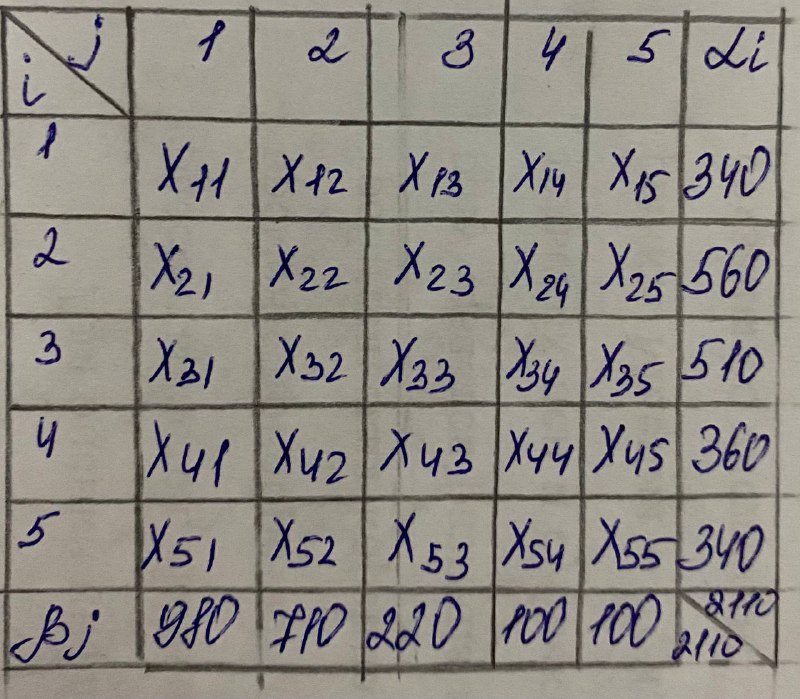
Рис. 1 – Экономико-математическая модель

Проверим условие баланса. Находим сумму площадей культур и площадей земель. Площади культур: 340 + 560 + 510 + 360 + 340 = 2110. Площади земель: 980 + 710 + 220 + 100 + 100 = 2110. Сумма площадей культур равна сумме площадей земель – модель задачи закрытая.

Составим ограничения. Первая группа ограничений по культурам:

1. X₁₁ + X₁₂ + X₁₃ + X₁₄ + X₁₅ = 340

2. X₂₁ + X₂₂ + X₂₃ + X₂₄ + X₂₅ = 560

3. X₃₁ + X₃₂ + X₃₃ + X₃₄ + X₃₅ = 510

4. X₄₁ + X₄₂ + X₄₃ + X₄₄ + X₄₅ = 360

5. X₅₁ + X₅₂ + X₅₃ + X₅₄ + X₅₅ = 340

Вторая группа ограничений по землям:

6. X₁₁ + X₂₁ + X₃₁ + X₄₁ + X₅₁ = 980

7. X₁₂ + X₂₂ + X₃₂ + X₄₂ + X₅₂ = 710

8. X₁₃ + X₂₃ + X₃₃ + X₄₃ + X₅₃ = 220

9. X₁₄ + X₂₄ + X₃₄ + X₄₄ + X₅₄ = 100

10. X₁₅ + X₂₅ + X₃₅ + X₄₅ + X₅₅ = 100

Так как критерий оптимальности – интенсивность смыва почвы при размещении на землях определенной категории, то целевая функция примет вид:

Z = 1,8X₁₁ + 4,7X₁₂ + 10,2X₁₃ + 30,5X₁₄ + 61,4X₁₅ + 2,4X₂₁ + 6,3X₂₂ + 12X₂₃ + 34X₂₄ + 64X₂₅ + 0,2X₃₁ + 0,8X₃₂ + 2,4X₃₃ + 4,8X₃₄ + 6,4X₃₅ + 2,3X₄₁ + 6,3X₄₂ + 11,8X₄₃ + 33,5X₄₄ + 64X₄₅ + 3,8X₅₁ + 10X₅₂ + 30X₅₃ + 60X₅₄ + 80X₅₅.

Составим первый опорный план методом наименьшего элемента.

Суть этого метода – на каждом шаге алгоритма поиска опорного решения стараться занять максимально возможным ресурсом прежде всего клетки, в которых лежат наименьшее значение Cij (рис.2).

Рис. 2 – Метод наименьшего элемента

При использовании метода наименьшего элемента было получено следующее опорное решение: X12 =340, X21=110, X22 =370, X23=80, X31=510, X41=360, X53=140, X54=100, X55=100.

Найдем значение целевой функции:

Z=340*4,7+110*2,4+370*6,3+80*12+510*0,2+360*2,3+140*30+100*60+100*80=24283

Проверим решение по количеству занятых клеток:

Кзан = 9; (m+n-1) = (5+5-1) = 9

Кзан = (m+n-1) → решение базисное, невырожденное.

Далее составим опорный план методом Фогеля.

Суть метода аппроксимации Фогеля заключается в следующем. Для каждой строки и для каждого столбца находим разности между двумя записанными в них минимальными тарифами. Полученные разности записываем в специально отведенные для этого столбце и в строке в таблице условий задачи. Среди указанных разностей выбираем максимальную. В строке (или в столбце), которой данная разность соответствует, определяем минимальный тариф. Клетку, в которой он записан, заполняем.

Применение метода аппроксимации Фогеля позволяет получить либо опорный план, близкий к оптимальнму, либо сам оптимальный план (рис. 3).

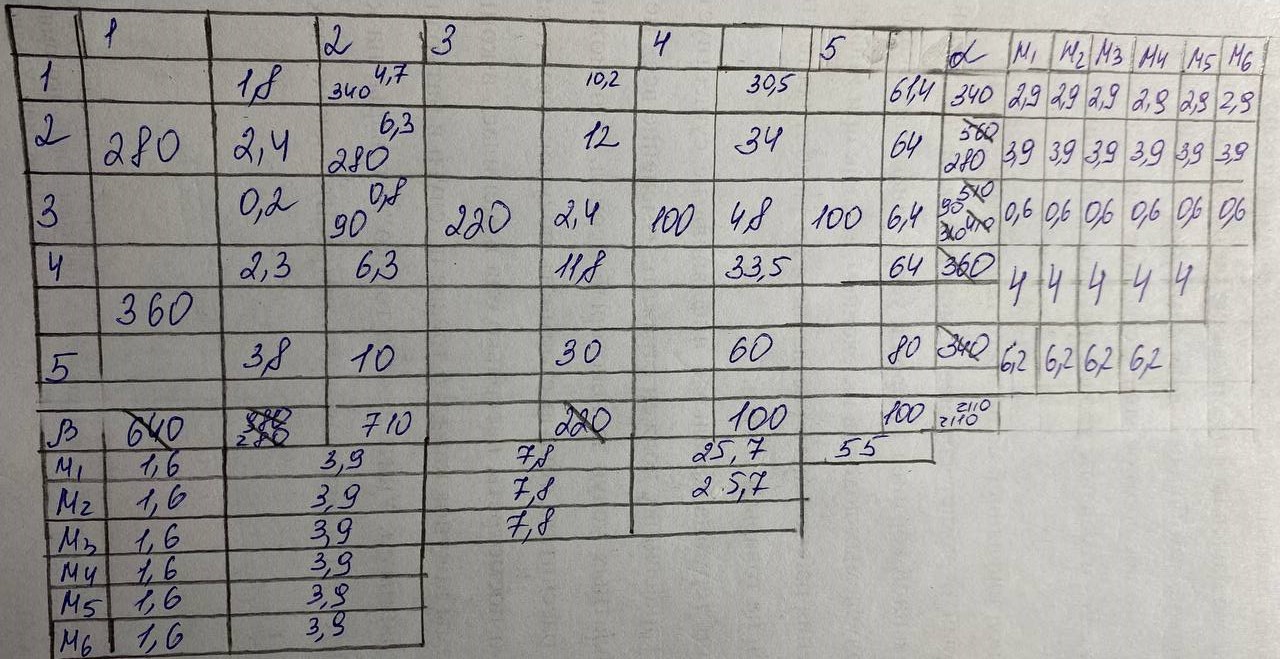
Рис. 3 – Метод Фогеля

При использовании метода Фогеля было получено следующее опорное решение: X21 =280, X41=360, X51=340, X12=340, X22=280, X32=90, X33=220, X34=100, X35=100.

Найдем значение целевой функции:

Z=280*2,4+360*2,3+340*3,8+340*4,7+280*6,3+90*0,8+220*2,4+4,8*100+6,4*100=7874

Так же, как и в методе наименьшего элемента, проверим решение по количеству занятых клеток:

Кзан = 9;

(m+n-1) = (5+5-1) = 9

Кзан =(m+n-1) → решение базисное, невырожденное.

Проверим решение, полученное методом наибольшего элемента, на оптимальность. Для этого используем метод потенциалов (рис. 4).

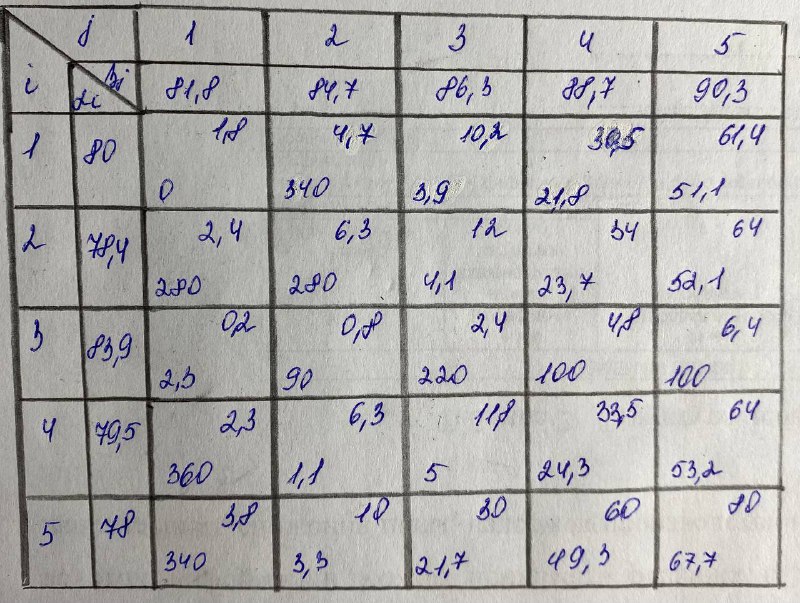
Рис.4 – Проверка методом потенциалов

Если сравнить значения целевых функций в опорных планах, полученных методом наименьшего элемента и методом Фогеля, можно увидеть, что меньшее из них соответствует методу Фогеля и равен 7874.

Сделаем проверку, решив задачу в ПП MS Excel.

Для начала заполняем две таблицы: «Матрица культур» и «Матрица распределения земель» (рис.5).

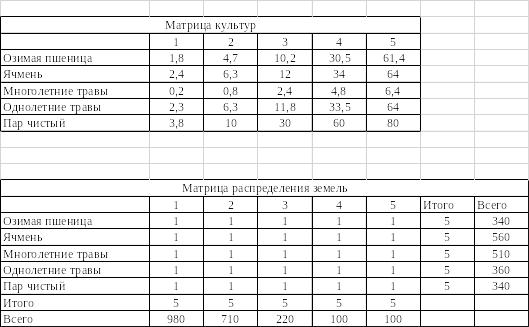
Рис. 5 – Матрица культур и Матрица распределения земель

Заполняем «Расчетную матрицу». Для этого копируем «Матрицу распределения земель», не захватывая строку и столбец Всего. В каждой ячейке удаляем единицу и находим значение, умножая озимую пшеницу из «Матрицы культур»» на озимую пшеницу из Матрицы распределения земель» (рис.6).

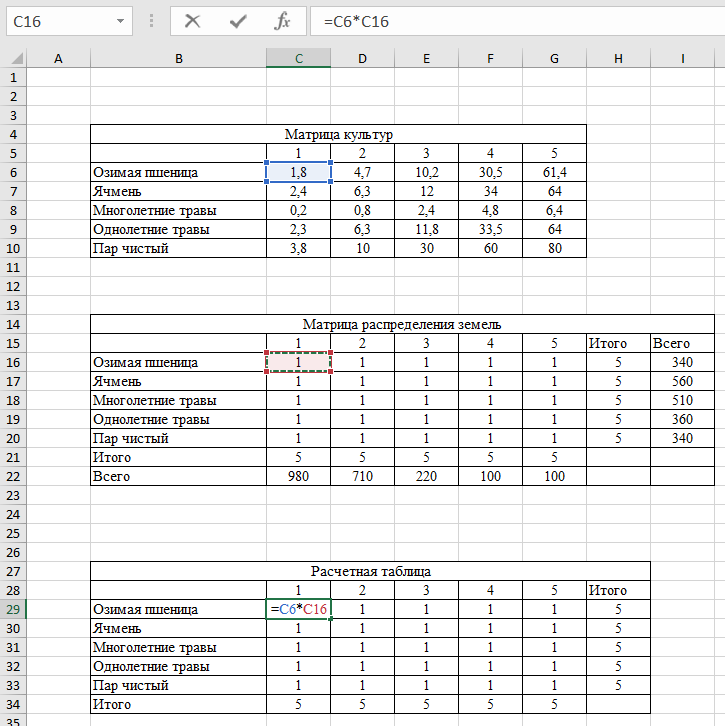
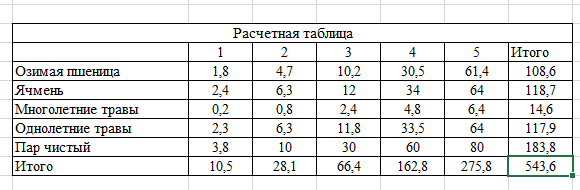
Рис. 6 – Расчетная матрица

Для того, чтобы найти оптимальное решение, выделяем ячейку Н34 и заполняем «Параметры поиска решений» (рис. 7).

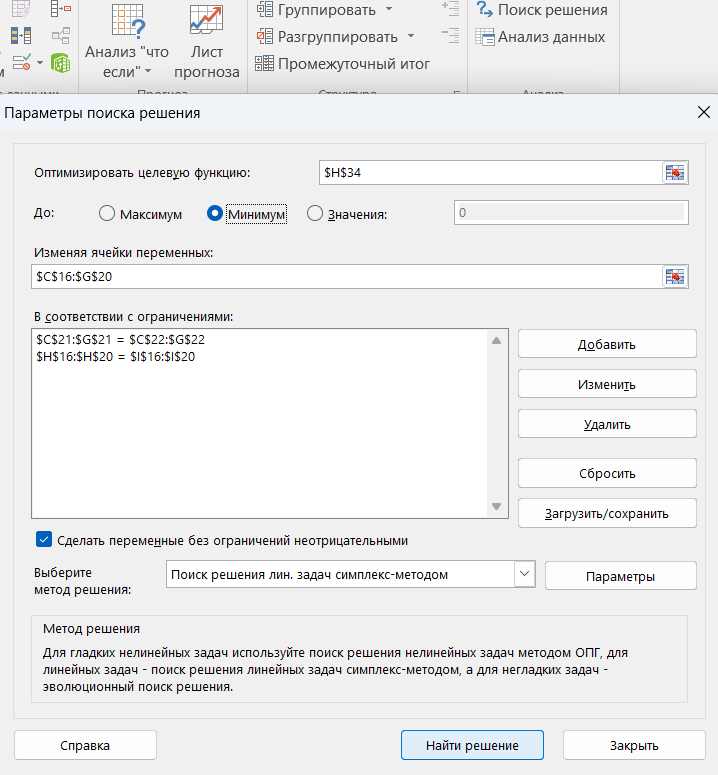
Рис. 7 – Параметры поиска решений

После нахождения решения появляется диалоговое окно «Результаты поиска решения» и мы получаем ответ (рис. 8).

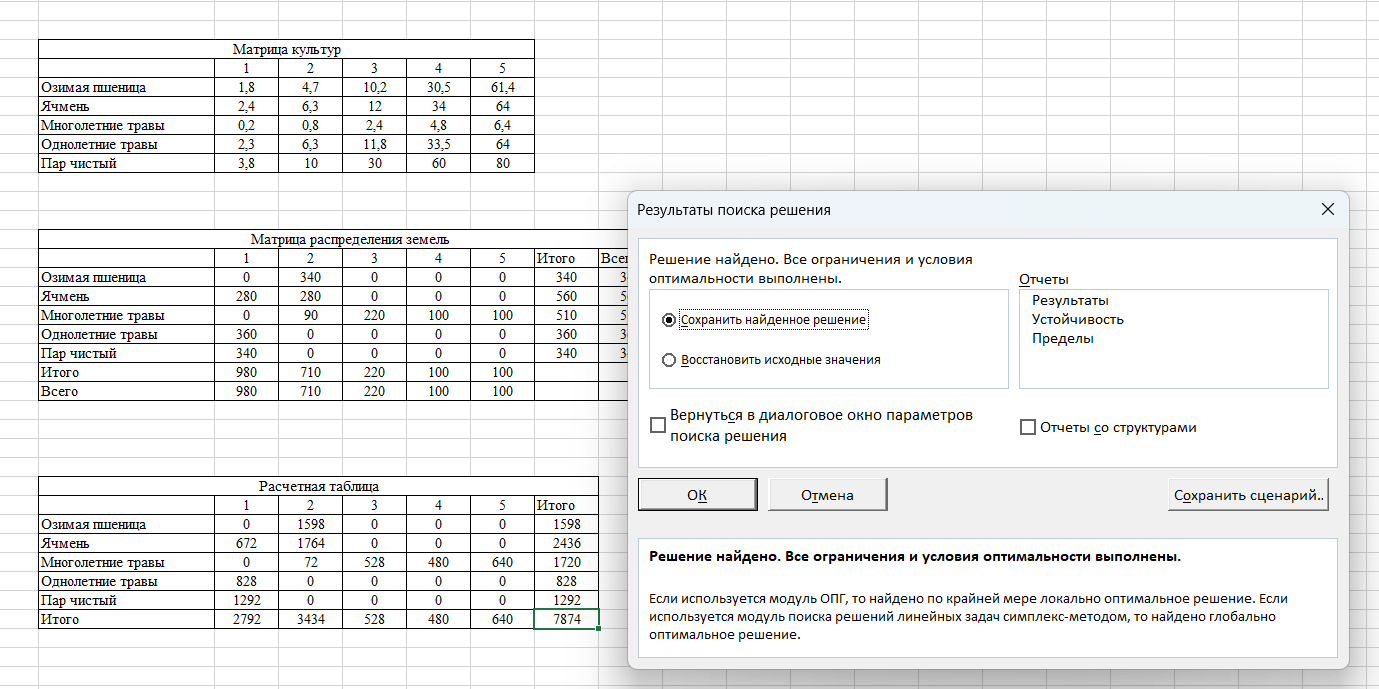
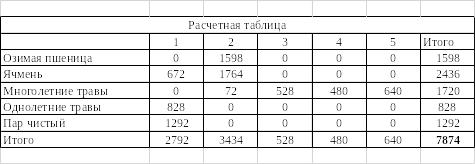
Рис. 8 – Результаты поиска решений

Согласно полученным данным, оптимум составил 7874. Такое же значение мы получили с помощью метода Фогеля. Следовательно, можно сделать вывод о том, что решение, полученное методом Фогеля, ближе к оптимальному.