Большой биофизический практикум 2024 / Лабораторная работа № 9 (бф)

Аннотация

В данной лабораторной работе были проведены вычислительные исследования структурных и энергетических характеристик молекул флавинмононуклеотида (ФМН), его аналога рибофлавина и ФМН, взятого из кристаллической структуры комплекса с люциферазой. Для оптимизации геометрии молекул использовались методы молекулярной механики в программе HyperChem. В процессе работы были выполнены вычисления энергии и градиента для каждой молекулы, а также сравнительный анализ полученных данных. Полученные результаты позволили определить, что молекулы ФМН и ФМН, взятый из комплекса люциферазы, имеют одинаковую энергетическую стабильность, в то время как рибофлавин, обладая меньшей энергией, оказался более устойчивым в вакууме. Эти данные являются основой для дальнейшего анализа и оценки структуры биомолекул.

Материалы и методы

Материалы:

1. Молекулы флавинмононуклеотида (ФМН), взятые из базы данных ChemSpider (ID:559060) и из кристаллической структуры комплекса люциферазы (PDB ID:3FGC).

2. Молекула рибофлавина, полученная из базы данных ChemSpider.

Методы:

1. Программа для расчетов: Все вычисления были выполнены с использованием программы HyperChem, которая включает методы молекулярной механики, квантовой химии и молекулярной динамики.

2. Молекулярная механика: Для оптимизации геометрии молекул использовался метод молекулярной механики с силовым полем AMBER, который описывает взаимодействия атомов в молекуле с использованием эмпирически заданных потенциальных функций.

3. Минимизация энергии: Минимизация энергии молекул была проведена с помощью алгоритма Polak-Ribiere для оптимизации структуры молекул. При этом был использован критерий сходимости на основе значений градиента (RMS) с установленным порогом 0.1. Минимизация продолжается до достижения локального минимума энергии молекулы.

4. Одноточечное вычисление: Для каждого исследуемого вещества было выполнено одноточечное вычисление для оценки полной энергии молекулы в ее исходной структуре до оптимизации.

Ход работы

3) Измерение геометрии молекулы

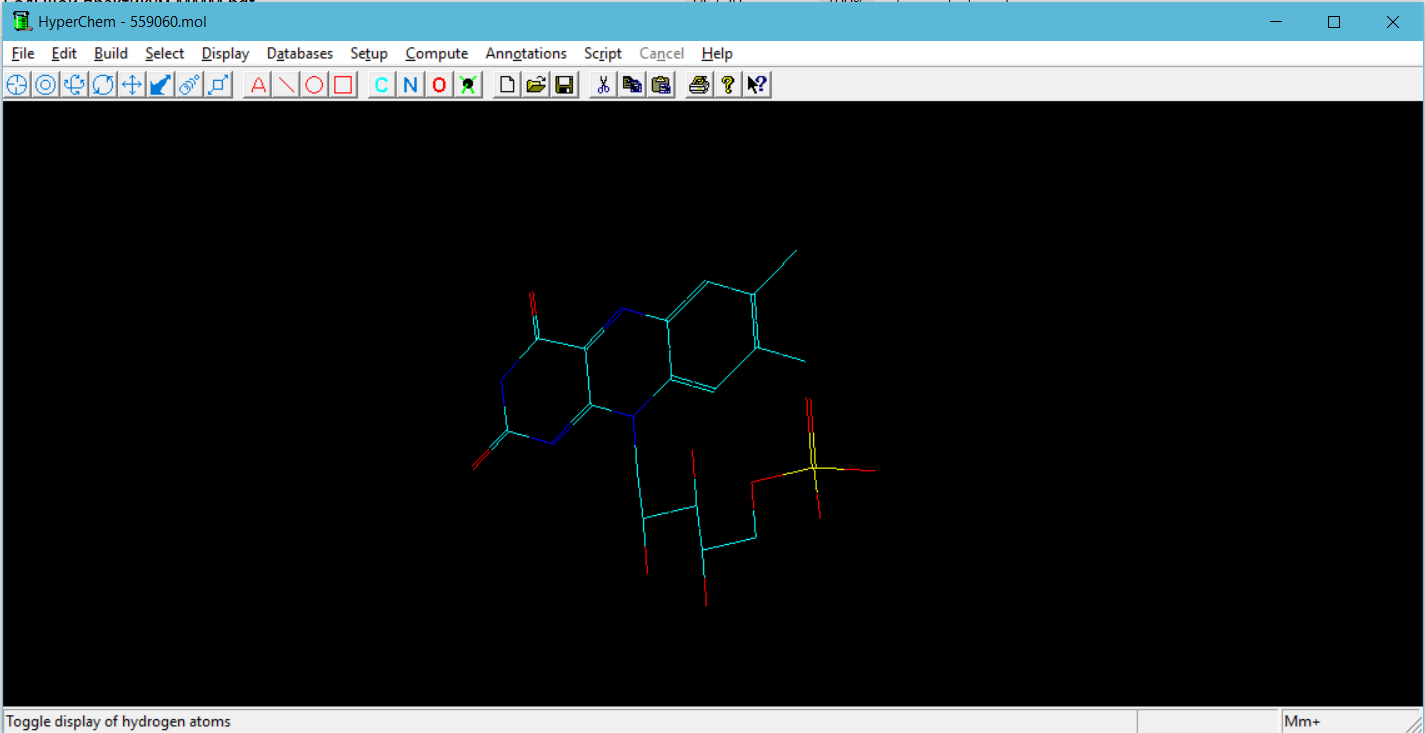
Геометрия молекулы:

Одиночное вычисление:

5) Оптимизация молекулы

6)Сравнение

Energy = 75.25 kcal/mol Gradient = 26.06

Energy = 44.64 kcal/mol Gradient = 0.58

7)

8) Минимизация структуры ФМН

Energy = 44.64 kcal/mol Gradient = 0.58

Energy = 49.30 kcal/mol Gradient = 2.50

9)

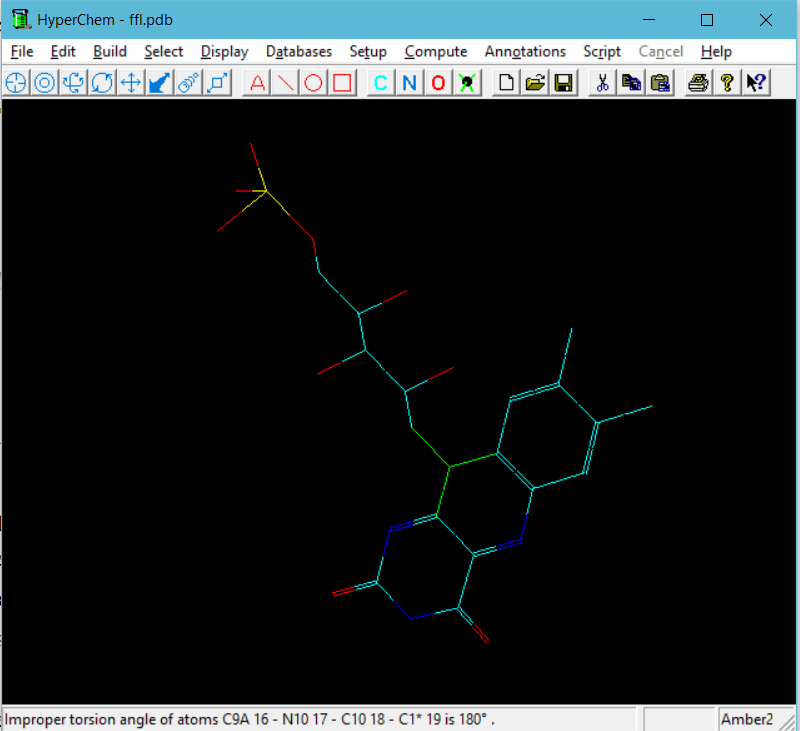
Energy = 83.25 kcal/mol Gradient = 0.25

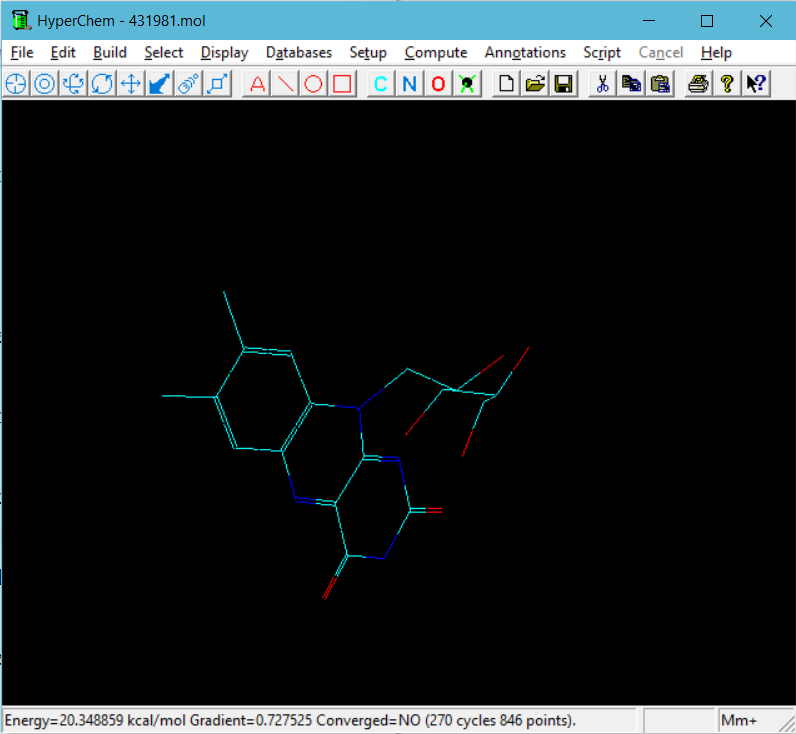
Energy = 20.34 kcal/mol Gradient = 0.72

Таблица 1.

	Energy	Gradient	Angle С11 N7 C12
Не опт-й ФМН	75.25	26.06	120.6
Опт-й ФМН	44.64	0.58	115.7
Минимиз ФМН	43.30	0.44	115.7
ФМН люц-а	72.25	25.2	119.2
Рибофлавин	20.34	0.72	114.8

Выводы:

1. Сравнение энергии молекул ФМН:

Энергии ФМН и ФМН, взятого из кристаллической структуры комплекса люциферазы, сильно не отличаются друг от друга. Что свидетельствует о том, что данные структуры находятся в одинаково устойчивом энергетическом состоянии.

Оптимизированная структура ФМН будет более устойчивой, как и минимизированная.

2. Сравнение ФМН и рибофлавина:

Энергия рибофлавина (20.34 kcal/mol) значительно ниже, чем у ФМН (44.64 kcal/mol). Это можно объяснить отсутствием фосфатной группы у рибофлавина, что приводит к меньшему числу межатомных взаимодействий и более низкой энергии системы. Рибофлавин, таким образом, является более устойчивым с точки зрения энергии в вакууме.

3. Значения градиентов:

Градиенты для всех молекул (0.58 для ФМН, 0.72 для рибофлавина) свидетельствуют о том, что оптимизация геометрии практически завершена, но небольшие отклонения от идеальных значений могут сохраняться.

Более высокий градиент у рибофлавина может быть связан с тем, что его структура менее сложна и оптимизация потребовала меньшего числа итераций.

4. Идентичные энергии ФМН и ФМН из комплекса люциферазы говорят о том, что кристаллическая среда минимально влияет на структуру ФМН. Для рибофлавина достигнута наиболее низкая энергия среди всех исследуемых молекул, что делает его наиболее устойчивой конформацией в вакууме.

5. Объекты с минимальными значениями углов (Рибофлавин, Опт-й ФМН и Минимиз ФМН) имеют более оптимизированную и компактную геометрию, тогда как Не опт-й ФМН с максимальным углом обладает наибольшими структурными искажениями.

6. Двухгранные углы:

Двугранный угол - это угол между двумя пересекающимися плоскостями или полуплоскостями. В химии это угол по часовой стрелке между полуплоскостями через два набора из трех атомов, имеющих два общих атома. В геометрии твердых тел это определяется как объединение прямой и двух полуплоскостей, у которых эта линия является общим ребром.

Контрольные вопросы:

1) Какие методы вычислительной химии вы знаете? В чем их особенности и различия?

Методы вычислительной химии делятся на три основные группы по степени строгости приближений и потребности в вычислительных ресурсах:

• Молекулярная механика: основывается на классической механике. Атомы описываются как материальные точки с массой и зарядом, а их взаимодействия моделируются с использованием потенциальных функций (например, растяжение связей, деформация углов). Этот метод прост, быстр, но ограничен в точности и применим лишь к системам, параметры которых уже эмпирически изучены.

• Полуэмпирические квантово-химические методы: используют упрощенные квантово-механические уравнения и эмпирические параметры для ускорения расчетов. Эти методы более точны, чем молекулярная механика, но требуют больше вычислительных ресурсов.

• Неэмпирические (ab initio) методы: полностью основаны на квантовой механике и используют строгие математические подходы, такие как решения уравнения Шрёдингера. Эти методы наиболее точны, но чрезвычайно затратны по времени и вычислительным ресурсам.

2) Что такое силовое поле? Какие потенциальные функции может содержать силовое поле молекулярной механики?

Силовое поле — это набор потенциальных функций, описывающих взаимодействия атомов в молекуле. Оно включает параметры, которые эмпирически определяются для описания поведения различных типов связей и взаимодействий.

Потенциальные функции в силовом поле включают:

• Растяжение связей: описывает изменения длины связей (обычно гармоническая функция по закону Гука).

• Угловая деформация: описывает изменения валентных углов.

• Торсионные взаимодействия: моделируют внутреннее вращение вокруг связей.

• Невалентные взаимодействия:

  • Ван-дер-Ваальсовы силы (притяжение на больших расстояниях и отталкивание на коротких).

  • Электростатические взаимодействия (заряды атомов).

  • Водородные связи.

3) В чем состоит приближение Борна-Оппенгеймера? Что такое поверхность Борна-Оппенгеймера?

Приближение Борна-Оппенгеймера заключается в разделении движений электронов и ядер из-за большой разницы их масс и скоростей. Предполагается, что электроны движутся намного быстрее, чем ядра, и успевают адаптироваться к изменениям их положения.

Поверхность Борна-Оппенгеймера — это функция, описывающая зависимость энергии молекулы от координат ядер. В молекулярной механике это называют поверхностью потенциальной энергии, где минимумы соответствуют стабильным конформациям молекулы.

4) Как производится минимизация энергии молекулы? От чего может зависеть энергия оптимизированной конфигурации атомов?

Минимизация энергии молекулы осуществляется итерационным методом, где геометрия молекулы изменяется для достижения состояния с минимальной потенциальной энергией. Методы минимизации делятся на:

• Линейные (основаны на первых производных потенциальной энергии).

• Квадратичные (используют как первые, так и вторые производные).

Энергия оптимизированной конфигурации зависит от:

• Начальной структуры: минимизация найдет локальный минимум, ближайший к исходной геометрии.

• Метода расчета: различия в силовых полях и параметрах.

• Присутствия внешних факторов: например, растворителя.