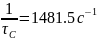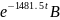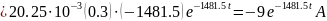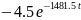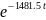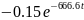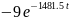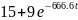2курс 2семестр / РГР 3 / ТОЕ задача 1
.DOCXЗадача 1
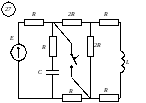
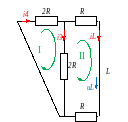
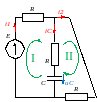
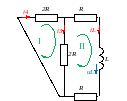
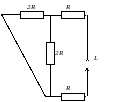
1. t 0 Аналізуємо схему до комутації, це перший усталений режим. Ключ розімкнений.
Так, як маємо справу із джерелом постійного ЕРС, то: L – закоротка у колі; С – розрив кола.
Відмітимо на схемі усі величини:
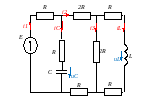 →
→
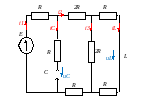 i1(-0)=
i2(0)=
i1(-0)=
i2(0)=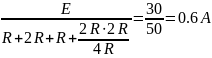 iL(-0)=
i3(-0)=0.3
A
iC(-0)=0
uL(-0)=0
uC(-0)=i2•
iL(-0)=
i3(-0)=0.3
A
iC(-0)=0
uL(-0)=0
uC(-0)=i2•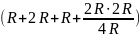 =0.6•40=24
B
=0.6•40=24
B
|
t=-0 До комутації |
t=0+ Вільні складові |
t>4.6τ Примушені складові |
i1(t) |
0.6 |
|
|
iL(t) |
0.3 |
|
|
iC(t) |
0 |
|
|
uL(t) |
0 |
|
|
uC(t) |
24 |
|
|
2. t 0+ Аналізуємо схему після комутації. Ключ замкнений. Схема розпадаєтьмя на дві окремі схеми RL та RC. Опрацьовуємо їх окремо
RC
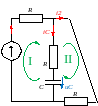
Складаємо систему рівнянь за законами Кірхгофа:
-i1+i2+iC=0 i1•R+uC=E i2•2R-uC=0
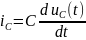
Отримаємо систему
диференційних рівнянь:
-i1+i2+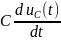 =0
i1•R+uC+uL=E
i2•2R-uC=0
=0
i1•R+uC+uL=E
i2•2R-uC=0
RL
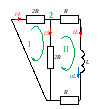
Складаємо систему рівнянь за законами Кірхгофа:
-i4+i3+iL=0 i4•2R+i3•2R =0 iL•R+ iL•R- i3•2R+ uL =0
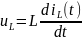
Отримаємо систему
диференційних рівнянь:
-i4+i3+iL=0
i4•2R+i3•2R
=0
2(iL•R)- i3•2R+
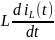 =0
=0
РІШЕННЯ: uC(t) = uC пр + uC в
uC(t)
= uC
пр +
A1 ˗ постійна інтегрування τС = С • RE ˗ cтала часу перехідного процесу для RC
|
РІШЕННЯ: iL(t) = iL пр+ iL в
iL(t)
=
iL
пр
+
A1 ˗ постійна інтегрування
τL
=
|
3. t > 4.6τ Аналізуємо схему після закінчення перехідного процесу. Знайдемо примушені складові загального рішення диф. рівняння. Так, як маємо справу із джерелом постійного ЕРС, то: L – закоротка у колі; С – розрив кола.
RC
i1
пр
= iC =0 A
uC
=
|
RL
iL
=0
A
uL
=
|
||
|
t=-0 До комутації |
t=0+ Вільні складові |
t>4.6τ Примушені складові |
i1(t) |
0.6 |
|
1.5 |
iL(t) |
0.3 |
|
0 |
iC(t) |
0 |
|
0 |
uL(t) |
0 |
|
0 |
uC(t) |
24 |
|
15 |
4. t 0 Аналізуємо схему у перший момент після комутації. Розпочався перехідний процес. Знайдемо вільні складові рішення диференційного рівняння:
RL
За першим законом комутації: uC(-0)= uC(0+)=24 B
uC(t)=
uC
пр
+ A1 У момент часу t=0+ uC(0+)= uC пр + A1 e0=1 тоді:
uC(0+)= uC пр + A1 24 = 15 + A1 → A1= 9 B
Знайдемо сталу часу для кола RC
τ
= С∙
Розрахуємо еквівалентний опір:
τ = С∙ = 25 ∙ 10-6 ∙60 = 1.5 мс
4,6 6.9 мс uC(t)= uC пр + A1
uC(t)=
15
+
5. Знайдемо струм конденсатора Візьмемо похідну:
|
RC
За першим законом комутації: iL(-0)= iL(0+)=0.3 A
iL
(t)=
iL
пр
+ A2 У момент часу t=0+ iL (0+)= iL пр + A2 e0=1 тоді:
iL (0+)= iL пр + A2 0.3 = 0 + A2 → A2= 0.3 B
Знайдемо сталу часу для кола RL
τ
=
Розрахуємо еквівалентний опір:
τ
=
=
0,675 18.4 мс iL (t)= iL пр + A2
iL(t)=
0.3
5. Знайдемо струм конденсатора Візьмемо похідну:
|
Знайдемо вільну складову струму i1(t) У колі RC у момент часу t=0+
За допомогою правила розкиду струмів знайдемо струм через джерело:
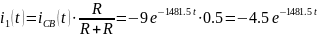 A
A
|
t=-0 До комутації |
t=0+ Вільні складові |
t>4.6τ Примушені складові |
i1(t) |
0.6 |
|
1.5 |
iL(t) |
0.3 |
0.3 |
0 |
iC(t) |
0 |
|
0 |
uL(t) |
0 |
|
0 |
uC(t) |
24 |
|
15 |
6.Побудуємо графіки
Схема RC
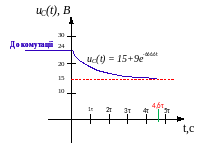
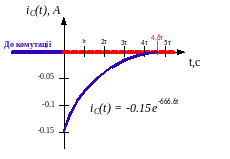
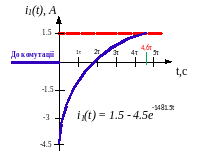
Схема RL
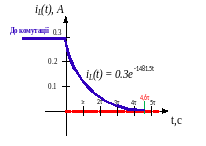
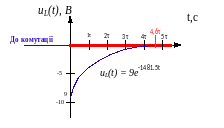
Порівняння двох ПП у колах RC та RL
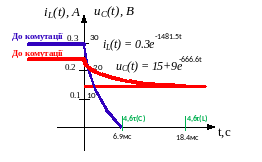 φ
φ

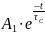
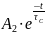
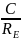 ˗
cтала
часу перехідного процесу для R
˗
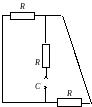
cтала
часу перехідного процесу для R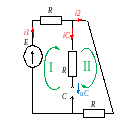
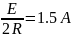
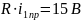
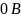
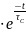
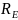
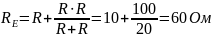
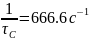
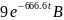
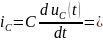
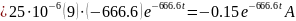
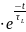
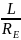
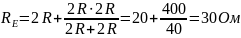
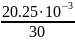 =
0.675
мс
=
0.675
мс