МСиП_лабораторные

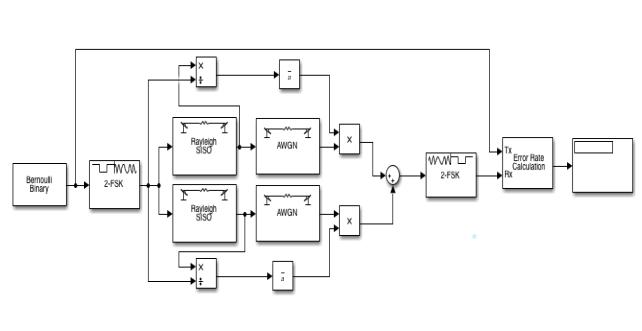
Результирующая схема модели показана на рисунке 82.

Рисунок 82 – Схема с оптимальным сложением двух ветвей

Снимите кривую помехоустойчивости для данного случая (диапазон изменения отношения /0 – от 0 до 14 дБ с шагом 2 дБ, менять этот параметр необходимо синхронно в двух блоках АБГШ-канала).

В завершение работы отредактируйте расположение блоков в окне модели, чтобы сделать ее более наглядной. Сохраните модель, присвоив ей подходящее имя, и перенесите изображение модели в созданный документ

Word, используя команду меню Edit Copy Current View to Clipboard Metafile в окне модели. То же сделайте с сохраненной ранее версией модели, содержащей блоки выбора максимально мощной ветви, получения гистограммы и оценки средней мощности сигнала.

61

Содержание отчета

1.Схемы двух созданных моделей с краткими комментариями о назначении их блоков.

2.Совместно построенные графики помехоустойчивости системы с некогерентной ЧМ-2 (для каждого случая необходимо на том же графике построить и теоретическую кривую по указанным далее

формулам; параметр или 0 в этих формулах соответствует отношению сигнал/шум на бит /0):

для случая АБГШ-канала;

для случая рэлеевского канала;

для случая двух рэлеевских ветвей приема с выбором максимально мощного сигнала;

для случая оптимального сложения двух рэлеевских ветвей приема.

3.Значение средней мощности сигнала и гистограмма ее статистического распределения для рэлеевского канала.

4.Значение средней мощности сигнала и гистограмма ее статистического распределения для случая выбора максимально мощного из двух независимых ветвей.

5.Выводы.

62

Лабораторная работа № 5

Моделирование систем связи в среде MATLAB

Цели работы

Получение навыков моделирования систем связи в среде MATLAB.

Исследование помехоустойчивости алгоритмов демодуляции для многоантенных систем MIMO.

Указания к выполнению работы

1.Построение модели многоантенных систем связи в среде MATLAB

MIMO (Multiple Input Multiple Output) – метод пространственного

кодирования сигнала, позволяющий увеличить полосу пропускания канала, при котором передача данных осуществляется с помощью N антенн и их приёма М антеннами. Передающие и приёмные антенны разнесены настолько, чтобы достичь слабой корреляции между соседними антеннами.

Применение технологий MIMO решает две задачи:

увеличение качества связи за счет пространственного временного/ частотного кодирования и (или) формирования лучей

(beamforming);

повышение скорости передачи при применении пространственного мультиплексирования.

Вразличных реализациях MIMO имеется в виду одновременная передача

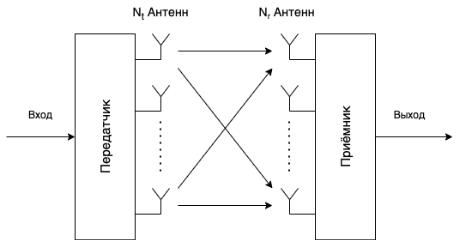
водном физическом канале нескольких независимых сообщений. С целью реализации действия MIMO применяют многоантенные системы: на передающей стороне имеется передающих антенн, а на приемной стороне приемных. Данная структура приведена на рисунке 83.

Рисунок 83 – Структура MIMO

63

Приступим к построению модели. Запустите программу MATLAB, в открывшемся окне на панели инструментов щелкните на иконку New Script (рисунок 84).

Рисунок 84 – Иконка New Script на панели инструментов

Появится пустое окно новой модели (рисунок 85).

Рисунок 85 – Пустое окно нового скрипта

Для начала напишем команды, которые будут очищать весь текст из окна командной строки при запуске новой программы.

clc; clear;

Для начала определим параметры для моделирования:

количество передающих и приемных антенн,

количество каналов,

выходную мощность базовой станции,

диапазон отношения энергии сигнала к энергетической спектральной плотности шума ( ⁄0),

количество битов на один символов (размер созвездия)

64

Nt = 4; % передающие антенны Nr = 4; % приёмные антенны

Kch = 4;

Es = 1; % мощность БС

EbNoVec = 5:5:30; % диапазон Eb/N0

modOrd = 2; % количество бит на один символ

hStr = RandStream('mt19937ar'); % For random objects

Переходим к настройке симуляции:

Создаем системные объекты QAM-модулятора и QAM-демодулятора.

% Создание QAM-модулятор

hMod = comm.RectangularQAMModulator(...

'ModulationOrder', 2^modOrd, ...

'PhaseOffset', 0,'BitInput',true, 'NormalizationMethod',

'Average power');

% Создание QAM-демодулятор

hDemod = comm.RectangularQAMDemodulator(...

'ModulationOrder', 2^modOrd, ...

'PhaseOffset', 0,'BitOutput',true, 'NormalizationMethod', 'Average power');

Создаем системные объекты расчета частоты ошибок для приемника

hBERCalc = comm.ErrorRate('ComputationDelay',modOrd);

Также предварительно выделим переменную для хранения результатов BER, чтобы увеличить скорость выполнения симуляции

BER_final = zeros(length(EbNoVec), 3);

Настроим параметры рисунка для визуализации результатов BER.

h = gcf; % возвращает дескриптор текущего рисунка

grid on; % отображает основные линии сетки для текущих осей hold on; % сохраняет графики в текущих осях

ax = gca; ax.YScale = 'log'; % устанаваливаем логарифмический масштаб для оси Y xlim([EbNoVec(1)-0.01 EbNoVec(end)]); ylim([1e-3 1]); % устанавливает ограничения по оси X и Y

xlabel('Eb/No (dB)'); ylabel('Uncoded BER'); % метки для осей X и Y h.NumberTitle = 'off'; % убираем номер фигуры

h.Renderer = 'zbuffer';

h.Name = 'Precoding'; % устанавливаем имя фигуры % устанавливаем название графика

title(['MU-MIMO ', num2str(Ntx), 'x', num2str(Ntx/Kch), 'x', num2str(Kch), ' QAM-', num2str(modOrd^2)]);

2. Модели системы MIMO.

Предполагается, что сигналы на передающей стороне излучаются одновременно и в одной полосе частот через M передающих антенн. Дискретная во времени модель канала включает в себя:

[ ]: символ, передаваемый µ-й антенной, индекс времени k ;

,: характеристика канала – комплексный коэффициент передачи тракта распространения сигнала между µ-й передающей и -й

65

приемной антеннами. Амплитуда | ,| имеет распределение Рэлея, коэффициент передачи канала представляет собой комплексную переменную с гауссовским законом распределения вероятности;

[ ]: выборка аддитивного белого гауссовского шума (АБГШ) на приемной -й антенне в момент времени k;

[ ]: принимаемый символ -й антенной в момент времени k.

Векторно-матричная модель определяет:

передаваемый вектор: [ ] = [ 1[ ], … , [ ]] ;

вектор шума: [ ] = [ 1[ ], … , [ ]] ;

принимаемый вектор: [ ] = [ 1[ ], … , [ ]] .

Матрица канала записывается в виде:

Уравнение наблюдения определяется как:

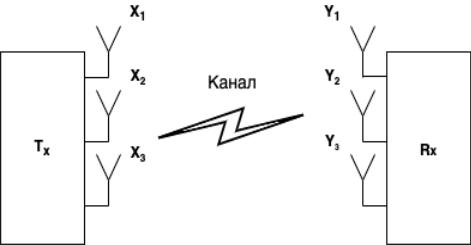
Модель канала изображена на рисунке 86.

Рисунок 86 – Пространственное мультиплексирование сигнала

66

3.Алгоритм МСКО.

Алгоритм демодуляции МСКО (МСКО, или Minimum MeanSquare Error –

где × – множество комплексных матриц размерности N×M. Из выражения (5.4) следует, что задача поиска оптимальной матрицы WМСКО сводится к задаче

минимизации действительной скалярной функции ( ) = {‖ − ‖2} комплексного матричного аргумента . Функция ( ) называется среднеквадратической функцией ошибки и может быть записана в следующей форме:

где (∙) – след матрицы (равен сумме ее диагональных элементов).

Функция ( ) является квадратичной и имеет ровно один минимум. Точку этого минимума можно найти традиционным методом, приравняв нулю

оптимального оценивания по критерию минимума среднеквадратической ошибки.

Выражение для корреляционной матрицы принятого вектора y нетрудно получить, подставив в первое уравнение (5.7):

67

переданным вектором s информационных символов, выражение (5.9) можно переписать в следующей форме:

В (5.10) учтено, что мощность сигнала, излучаемого каждой передающей антенной, предполагается равной единице (т.е. { ′} = 1). Выражение для взаимной корреляционной матрицы переданного вектора s информационных символов и принятого вектора y можно аналогично получить подстановкой во второе уравнение (5.7):

После подстановки (5.10) и (5.11) в (5.8) получим следующее выражение для матрицы WМСКО:

Подставляя (5.15) в (5.14), после несложных преобразований получим окончательное выражение для корреляционной матрицы ошибок оценивания (демодуляции) по методу МСКО:

68

reset(hBERCalc);

snrIndB = EbNoVec(idx) + 10*log10(modOrd); snrLinear = 10^(0.1*snrIndB);

disp_noise = 1/snrLinear;

while (BER_final(idx, 3) < 10000) || (BER_final(idx, 2) < 1) msg = randi([0 1], [Nrx*modOrd, 1]);

s = step(hMod, msg);

H = (randn(Nrx, Ntx) + 1i*randn(Nrx, Ntx))/sqrt(2); y = H*s;

rxSig = awgn(y, snrIndB, 0, hStr);

G = H'*inv(H*H'+((Ntx)*disp_noise)*eye(Ntx)); UE = G*rxSig;

demod = step(hDemod, UE);

BER_final(idx, :) = step(hBERCalc, msg, demod); display(BER_final);

end

semilogy(EbNoVec(1:idx), BER_final( 1:idx, 1), 'm^', 'linewidth', 1); drawnow;

end

В цикле выше на рисунке строим точки графика, сейчас необходимо их соединить линией и это можно сделать следующим образом:

semilogy(EbNoVec, BER_final( :, 1), 'm-^', 'linewidth', 1); hold off;

Запустите скрипт симуляции и наблюдайте за изменениями точек BER на графике. После окончания выполнения скрипта сохраните модель, присвоив ей подходящее имя, и перенесите изображение графика в созданный документ Word, используя команду меню File Save As в окне графика.

4.Исследование помехоустойчивости алгоритмов демодуляции для многоантенных систем MIMO.

Модифицируйте скрипт модели, измените тип модуляции с QAM-4 на QAM-16 и QAM-64, при этом диапазон отношения энергии сигнала к энергетической спектральной плотности шума ( ⁄0) оставьте таким же.

Запустите скрипты симуляции с соответствующими типами модуляций и наблюдайте за изменениями точек BER на графике. После окончания выполнения перенесите изображение графиков в созданный документ Word, используя команду меню File Save As в окне графика.

69

Содержание отчета

1.Скрипты трех моделей с краткими комментариями используемых функций.

2.Построенные графики помехоустойчивости каждой модели.

3.Выводы.

Список литературы

1.Бакулин М.Г., Варукина Л.А., Крейнделин В.Б. Технология MIMO: принципы и алгоритмы. – М.: Горячая линия – Телеком, 2014. – 244 с., ил.

2.Скляр Б. Цифровая связь. Теоретические основы и практическое применение / пер. с англ. - М.: Издательский дом «Вильямс», 2003.

3.Сергиенко А.Б. Цифровая связь: учебное пособие. - СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2012.

4.Прокис Дж. Цифровая связь. Пер. с англ./ Под ред. Д.Д. Кловского. - М.: Радио и связь, 2000. – 797 с.

70