ГУАП

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

доцент, канд. техн. наук, доцент				О.О. Жаринов
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №6

Основы цифровой фильтрации изображений. Метод фильтрации в спектральном пространстве

по курсу: МУЛЬТИМЕДИА ТЕХНОЛОГИИ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ гр. №
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2025

Цель работы: изучить основы обработки изображений на примере методов фильтрации, реализуемых в спектральном пространстве.

Краткие теоретические сведения о задачах обработки изображений и их практическом применении, а также о методе Фурье-фильтрации:

Фильтрация является одним из широко применяемых методов обработки изображений. Концептуальные идеи, положенные в основу методов фильтрации изображений, опираются на методологическую базу обработки одномерных сигналов, таких как аудио. Однако в отличие от задач фильтрации одномерных оцифрованных сигналов, которые представляют собой последовательность числовых значений, упорядоченную по времени появления каждого из них, последовательность значений пикселей изображения упорядочена лишь по возрастанию индексов строк и столбцов соответствующих матриц. Соответственно, если для временных сигналов период измеряется в секундах, а частота, соответственно, в Герцах ([Гц]=[1/c]), то применительно к изображениям период повторения группы пикселей и соответствующая периоду повторения пространственная частота (англ. space frequency) выражаются в условных безразмерных единицах. Тем не менее, для обработки изображений также успешно применяются подходы, связанные с избирательным воздействием на определенные частотные компоненты с целью целенаправленного изменения свойств изображения.

Методы фильтрации чаще всего используются для решения задачи улучшения качества изображений (увеличения резкости расфокусированных и смазанных изображений). Кроме того, фильтрация часто является одним из этапов более сложных, многоступенчатых методов обработки изображений, таких, например, как методы выделения границ объектов на изображениях.

Фильтрация всегда основана на наличии существенных различий в спектральном составе различных компонентов, составляющих исходное изображение. Для получения информации о частотном составе цифровых изображений существует специальный метод и алгоритм – двумерное быстрое преобразование Фурье (2D-БПФ). В результате его применения к массиву {xn,m} образуется массив значений его спектра {Xn,m}. Существует также и алгоритм обратного действия (обратное 2D-БПФ): по массиву значений спектра {Xn,m} можно вычислить массив значений пикселей изображения {xn,m}. В этом смысле концепция выглядит так же, как и в случае одномерного БПФ для обработки аудиосигналов. Расчет двумерного БПФ реализован в методе fft2() библиотеки numpy.

При реализации фильтрации изображений часто применяют метод фильтрации в спектральном пространстве (метод Фурье-фильтрации). Идея метода заключается в вычислении двумерного спектра {Xn,m} исходного изображения {xn,m}, последующей модификации спектра в соответствии заданными частотными характеристиками пространственного фильтра и формировании выходного изображения посредством вычисления обратного двумерного преобразования Фурье модифицированного спектра {Yn,m}.

Для модификации спектра исходного изображения {Xn,m} необходимо задать массив отсчетов двумерной дискретной передаточной функции фильтра {Wn,m} (его еще называют частотной маской), после чего выполнить преобразование

При задании массива {Wn,m} исходят из требований к свойствам, которые необходимо придать выходному изображению.

Фундаментом теории частотной фильтрации изображений является общая идея о том, что относительно крупным объектам на изображении соответствуют более низкие пространственные частоты, а мелким объектам и деталям – высокие частоты. Резкая граница между относительно ярким объектом и более темным окружающим фоном по своим частотным свойствам аналогична фронту одномерного импульсного сигнала, спектр такого фрагмента аудио имеет широкий спектр, в котором много высокочастотных составляющих.

Всегда важно помнить, что свойство комплексно-сопряженной симметрии двумерного БПФ требует обязательного выполнения такого же условия симметрии для массива {Wn,m}. В двумерном случае симметрия должна быть относительно точки, расположенной в центре, что программно реализуется сложнее, чем в одномерном случае. Для облегчения реализации принципа симметрии в библиотечном модуле numpy имеется специальный метод центрирования спектра fftshift(). При этом осуществляется двумерный циклический сдвиг спектра, таким образом, что компоненты спектра с нулевыми и/или максимальными индексами сдвигаются в центр матрицы спектра. Тогда при необходимости оставить в изображении только низкие частоты (т.е. оставить неизмененными протяженные объекты и уменьшить заметность мелких объектов), необходимо оставить в спектре только двумерную область, близкую к центру спектра, симметричную относительно центра (очевидно, что нужно быть очень аккуратным, т.к. в программе важно предусмотреть различные ветки кода для четных и нечетных размеров изображений по каждому размеру). Если же, наоборот, требуется выделить края (edges) объектов, а сами объекты сделать незаметными, то нужно оставить только высокие частоты, для чего следует уменьшить или вовсе сделать равными нулю значения спектра, находящиеся близко к центру матрицы. По окончании модификаций центрированного спектра обязательно осуществляется его обратный сдвиг (методом ifftshift()) и вычисляется двумерное обратное БПФ, в результате чего формируется отфильтрованное изображение, свойства которого нужным образом отличаются от исходного.

Метод Собеля — это дискретный оператор дифференцирования, применяемый для выделения границ на изображении. Его основная задача — вычислить приближённое значение градиента яркости изображения в каждой точке, чтобы обнаружить резкие изменения интенсивности, которые соответствуют границам объектов. Суть метода: изображение содержит области с разной интенсивностью (яркостью), границы объектов проявляются как резкие скачки яркости. Чтобы обнаружить такие изменения, вычисляется градиент изображения — то есть производная яркости по горизонтали и вертикали.

Горизонтальный градиент (изменения по X) рассчитывается путём свёртки изображения с ядром (фильтром):

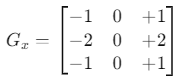
Это ядро свёртывается с изображением и вычисляет разность яркости между левыми и правыми пикселями.

Вертикальный градиент (изменения по Y) рассчитывается с помощью другого ядра:

Оно вычисляет разность между верхними и нижними пикселями.

Итоговый градиент (сила границы): Комбинируются оба результата, чтобы получить полную "силу" границы в каждой точке изображения. Обычно это делается с помощью формулы:

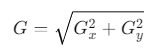
Эта величина показывает, насколько резко изменилась яркость в данной точке. Чем больше значение G, тем вероятнее, что в этом месте находится граница.

Альтернативно, для упрощения вычислений иногда используется приближённая формула:

Высокие значения градиента соответствуют границам объектов (местам, где интенсивность резко меняется). Низкие значения градиента означают однородные области без явных границ [6].