ГУАП

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

доцент, канд. техн. наук, доцент				О.О. Жаринов
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №4

Применение формирующих фильтров для создания шумоподобных аудиосигналов

по курсу: МУЛЬТИМЕДИА ТЕХНОЛОГИИ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ гр. №
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2025

Цель работы: изучить методологию создания шумоподобных сигналов на основе формирующих фильтров.

Краткие теоретические сведения о методе формирующего фильтра и классификации “окрашенных” шумов

Одним из возможных подходов к созданию шумоподобных аудиосигналов является метод формирующего фильтра. Основная идея метода заключается в пропускании через фильтр сигнала от искусственного создаваемого источника белого шума (БШ). В зависимости от свойств применяемого фильтра выходной сигнал оказывается “спектрально окрашенным”, что порождает специфические слуховые ощущения. Например, если применить полосовой фильтр с узкой полосой, то выходной шум будет восприниматься как “звенящий”, если применить фильтр нижних частот (lowpass), то аудиосигнал на выходе представляет собой глухой шум, напоминающий, в зависимости от параметров фильтра, шум водопада, фонтана, шелест листвы, и т.д. Смешивание нескольких шумов в разных пропорциях, а также динамическое изменение интенсивности одного или нескольких процессов значительно увеличить разнообразие формируемых звуковых эффектов [1].

Цветовые соответствия различных типов шумового сигнала определяются с помощью графиков спектральной плотности, то есть распределения мощности сигнала по частотам [2].

Ход работы:

Была разработана программа для генерации и обработки аудиосигнала, его фильтрации и амплитудной модуляции (Листинг 1).

Программа создает два независимых белых шумовых сигнала (БШ1 и БШ2) с равномерным распределением амплитуд в диапазоне [−1,1]. Дискретизация осуществляется с частотой Fd=44100, а длительность сигнала составляет 5 секунд.

Фильтрация сигналов выполняется с помощью цифровых фильтров Баттерворта второго порядка. Для первого шума (БШ1) применяется полосовой фильтр в диапазоне 2000–2025 Гц, а для второго шума (БШ2) – фильтр верхних частот с граничной частотой 0.8 Гц. Фильтрация производится с использованием представления секций (sos) и функции signal.sosfilt из библиотеки SciPy.

После фильтрации выполняется амплитудная модуляция сигнала y1​ с использованием сигнала y2​, обеспечивая вариации амплитуды без полного затухания путем добавления единицы к модулирующему сигналу.

Для предотвращения выхода значений за границы диапазона [−1,1] результат нормируется по максимальной амплитуде. Итоговый обработанный сигнал сохраняется в файл output.mp3 с помощью библиотеки soundfile.

Листинг 1 – Программа для модуляции и сохранения сигнала

import numpy as np

import matplotlib.pyplot as plt

from scipy import signal

import soundfile as sf

plt.close('all')

Fd = 44100

T = 5

N = round(Fd*T)

t = np.linspace(0, T, N)

x1 = np.random.uniform(low=-1.0, high=1.0, size=(2, N)) # БШ1

x2 = np.random.uniform(low=-1.0, high=1.0, size=(2, N)) # БШ2

# Задаем граничные частоты полос двух форм. фильтров:

f_dn1, f_up1 = 2000, 2025

f_up2 = 0.8

order1, order2 = 2, 2

sos1 = signal.butter(order1,

Wn=(f_dn1 / (Fd/2), f_up1 / (Fd/2)),

btype='bandpass', output='sos')

sos2 = signal.butter(order2,

Wn=(f_up2 / (Fd/2)),

btype='highpass', output='sos')

y1 = signal.sosfilt(sos1, x1)

y2 = signal.sosfilt(sos2, x2)

# модуляция одного процесса другим 1+ нужно, чтобы громкость не спадала до нуля

y = y1 * (1+y2)

# Нормировка:

Norm = np.max(np.abs(y))

if Norm != 0:

y = y / Norm

# Записываем аудиофайл

sf.write('output.mp3', np.transpose(y), Fd)

Получился следующий звук: сигнализация с белым шумом, бегающим из одного уха в другое. Прослушать можно по ссылке 1 в приложении. Для визуализации временных и спектральных характеристик аудиосигнала была разработана программа (Листинг 2).

Для представления временной формы сигнала используется библиотека librosa, которая обеспечивает удобное отображение формы волны для обоих каналов (левого и правого) с различными цветами и уровнями прозрачности. Отображаются два графика: полный сигнал и его первые 0.5.

Для спектрального анализа вычисляется дискретное преобразование Фурье (FFT) для обоих каналов. Полученные спектры амплитуд нормируются и переводятся в децибелы с учетом фиктивного минимального значения (eps), предотвращающего логарифмирование нуля. Амплитудные спектры левого и правого каналов отображаются на одном графике.

Листинг 2 – Программа для визуализации характеристик

import librosa

from scipy.signal import ShortTimeFFT

from scipy.signal.windows import gaussian

start_t, stop_t = 0, T

fig, ax = plt.subplots(figsize=(12, 4))

librosa.display.waveshow(y[0, :], sr=Fd, color='b', ax=ax, alpha=0.6, label=f'Левый')

librosa.display.waveshow(y[1, :], sr=Fd, color='r', ax=ax, alpha=0.4, label=f'Правый')

ax.set(xlim=[start_t, stop_t],

title='Сигнал',

xlabel='Время (с)',

ylabel='Амплитуда')

ax.legend(loc='upper right', ncols=2)

ax.grid(True, which='both', ls='--', alpha=0.5)

plt.show()

start_t, stop_t = 0, 0.5

fig, ax = plt.subplots(figsize=(12, 4))

librosa.display.waveshow(y[0, :], sr=Fd, color='b', ax=ax, alpha=0.6, label=f'Левый')

librosa.display.waveshow(y[1, :], sr=Fd, color='r', ax=ax, alpha=0.4, label=f'Правый')

ax.set(xlim=[start_t, stop_t],

title='Сигнал (первые 0.5 секунды)',

xlabel='Время (с)',

ylabel='Амплитуда')

ax.legend(loc='upper right', ncols=2)

ax.grid(True, which='both', ls='--', alpha=0.5)

plt.show()

# Вычисляем амплитудные спектры для обоих каналов:

Spectr_left = np.fft.fft(y[0, :])

Spectr_right = np.fft.fft(y[1, :])

# Корректные частоты (0..Fd/2):

N = len(y[0, :])

freq = np.fft.fftfreq(N, 1/Fd)[:N//2]

# Преобразуем в дБ:

def to_db(spectrum):

eps = 1e-9 # Фиксированное значение для избежания log(0)

return 20 * np.log10(np.abs(spectrum[:N//2]) + eps)

S_dB_left = to_db(Spectr_left)

S_dB_right = to_db(Spectr_right)

f = np.arange(0, Fd / 2, Fd / N) # Перевести Абсциссу в Гц

plt.figure(figsize=(12, 4))

plt.plot(f, S_dB_left, color="b",alpha=0.6, label='Левый канал')

plt.plot(f, S_dB_right, color="r",alpha=0.4, label='Правый канал')

plt.grid(True)

plt.minorticks_on() # отобразит мелкую сетку на лог.масштабе

plt.grid(True, which="major", color="#444", linewidth=1)

plt.axis([-500, 22500, -40, 80])

plt.xlabel('Частота (Гц)')

plt.ylabel('Уровень (дБ)')

plt.title("Амплитудный спектр")

plt.legend()

plt.grid(True, which='both', ls='--', alpha=0.5)

plt.show()

На рисунках 1 – 3 представлены визуализация сигнала во времени и амплитудный спектр получившегося звука.

Рисунок 1 – Полная визуализация сигнала

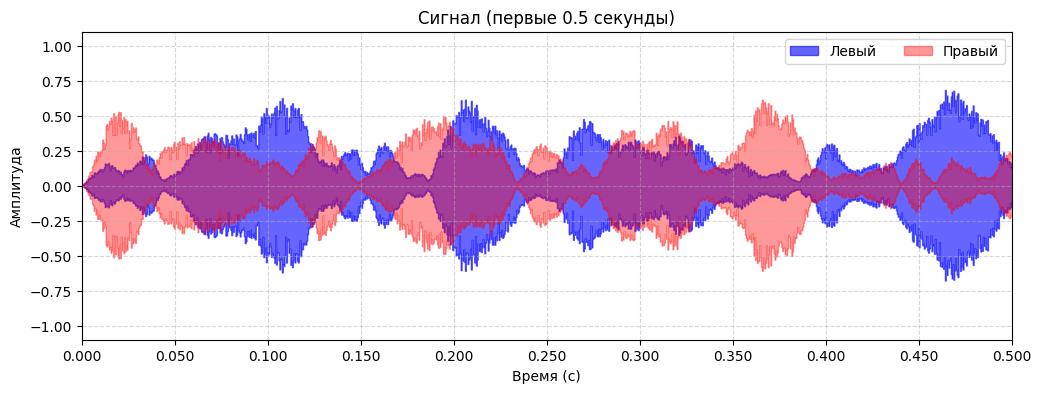
Рисунок 2 – Визуализация начального отрезка сигнала

Рисунок 3 – Визуализация амплитудного спектра

По графикам явно заметен “бегающий” шум.

Для модуляции следующего сигнала параметры были изменены следующим образом (Листинг 3): фильтрация с помощью цифровых фильтров Баттерворта для левого канала второго порядка, а правого – первого порядка. Для первого шума применяется полосовой фильтр в диапазоне 10000–15000 Гц, а для второго шума – фильтр нижних частот с граничной частотой 1000 Гц.

Листинг 3 – Фильтры для второго сигнала

f_dn1, f_up1 = 10000, 15000

f_up2 = 0.2

order1, order2 = 2, 1

sos1 = signal.butter(order1,

                     Wn=(f_dn1 / (Fd/2), f_up1 / (Fd/2)),

                     btype='bandpass', output='sos')

sos2 = signal.butter(order2,

                     Wn=(f_up2 / (Fd/2)),

                     btype='lowpass', output='sos')

Полученый сигнал звучит как синий шум, напоминает звук работы пескоструйного аппарата. На рисунках 4 – 6 представлена визуализация сигнала. Прослушать можно по ссылке 2 в Приложении.

Рисунок 4 – Полная визуализация сигнала

Рисунок 5 – Визуализация начального отрезка сигнала

Рисунок 6 – Визуализация амплитудного спектра

По графикам виден “ровный” шум в обоих каналах и применение полосового фильтра в диапазоне 10000-15000 Гц.

Для третьего сигнала параметры фильтров были настроены следующим образом (Листинг 4): для первого шума (БШ1) применяется полосовой фильтр второго порядка в диапазоне 100–200 Гц, позволяющий выделить сигналы в этом частотном диапазоне, для второго шума (БШ2) используется фильтр нижних частот первого порядка с граничной частотой 1 Гц, который подавляет частоты выше 1 Гц.

Листинг 4 – Фильтры для третьего сигнала

f_dn1, f_up1 = 100, 200

f_up2 = 1

order1, order2 = 2, 1

sos1 = signal.butter(order1,

Wn=(f_dn1 / (Fd/2), f_up1 / (Fd/2)),

btype='bandpass', output='sos')

sos2 = signal.butter(order2,

Wn=(f_up2 / (Fd/2)),

btype='lowpass', output='sos')

Получился звук, похожий на гул ветра в большом помещении вроде ангара. На рисунках 7 – 9 представлена визуализация. Прослушать можно по ссылке 3 в Приложении.

Рисунок 7 – Полная визуализация сигнала

Рисунок 8 – Визуализация начального отрезка сигнала

Рисунок 9 – Визуализация амплитудного спектра

По графику амплитудного спектра ярко заметно подавление правого канала.

Для создания сигнала с реверберацией были внесены следующие изменения (Листинг 5): фильтрация сигналов выполняется с помощью цифровых фильтров Баттерворта четвертого порядка для левого канала и второго порядка для правого канала, для первого шума применяется полосовой фильтр с диапазоном 1000–1100 Гц, для второго шума применяется фильтр нижних частот с граничной частотой 0.3 Гц. После фильтрации выполняется амплитудная модуляция сигнала y1 с использованием сигнала y2, что позволяет изменять амплитуду основного сигнала на основе модульного сигнала. Для этого применяется модуляция с параметром Fm = 0.9, где для каждого отсчета рассчитывается амплитудный коэффициент alfa, который изменяет громкость сигнала по схеме, основанной на косинусоидальных колебаниях с заданной частотой модуляции. Также в программе реализована задержка сигнала с применением параметра delay_samples. Сигнал задерживается на 0.5 секунды, что создает эффект эха.

Листинг 5 – Фильтры и модуляция сигнала с реверберацией

# Основные параметры

Fd = 44100 # Частота дискретизации (Гц)

T = 5 # Длительность сигнала (сек)

N = round(Fd * T) # Количество отсчетов

t = np.linspace(0, T, N)

x1 = np.random.uniform(low=-1.0, high=1.0, size=(2, N)) # БШ1

x2 = np.random.uniform(low=-1.0, high=1.0, size=(2, N)) # БШ2

f_dn1, f_up1 = 1000, 1100

f_up2 = 0.3

order1, order2 = 4, 2

sos1 = signal.butter(order1,

Wn=(f_dn1 / (Fd/2), f_up1 / (Fd/2)),

btype='bandpass', output='sos')

sos2 = signal.butter(order2,

Wn=(f_up2 / (Fd/2)),

btype='lowpass', output='sos')

# Применение фильтров

y1 = signal.sosfilt(sos1, x1)

y2 = signal.sosfilt(sos2, x2)

# Модуляция

y = y1 * (1 + y2)

alfa = np.zeros((2, N))

Fm = 0.9

for n in range(N):

alfa[:, n] = (0.5*(1-np.cos(2*np.pi*Fm*n/Fd)))**2

y = y * alfa

delay_samples = int(0.5 * Fd) # задержка

y[:, delay_samples:] += 0.3 * y[:, :-delay_samples]

Получившийся сигнал напоминает сонар подводной лодки. Прослушать можно по ссылке 4 в Приложении. Визуализация представлена на рисунках 9 - 11.

Рисунок 9 – Полная визуализация сигнала

Рисунок 10 – Визуализация начального отрезка сигнала

Рисунок 11 – Визуализация амплитудного спектра

По графикам видна реверберация и успешное применение полосового фильтра в диапазоне 1000-1100 Гц и фильтра нижних частот.

Вывод: в ходе выполнения лабораторной работы была изучена методология создания шумоподобных сигналов на основе формирующих фильтров. Были использованы полосовой фильтр, фильтр нижних частот, фильтр верхних частот. Успешно смоделированы четыре отличющихся сигнала.