МТ3

ГУАП

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

доцент, канд. техн. наук, доцент				О.О. Жаринов
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №3

Основы обработки аудиосигналов средствами Python. Применение рекурсивных фильтров

по курсу: МУЛЬТИМЕДИА ТЕХНОЛОГИИ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ гр. №
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2025

Цель работы: получить навыки обработки аудиосигналов на примере методов фильтрации сигналов во временной области с использованием рекурсивных цифровых фильтров.

Вариант 13:

Рисунок 1 – Вариант задания на фильтрацию сигнала

Краткие теоретические сведения о задачах обработки аудиосигналов и их практическом применении, а также о методах фильтрации:

Фильтрацию можно производить без вычисления спектра обрабатываемого оцифрованного аудиосигнала, непосредственно во временной области. В частности, уравнение работы рекурсивного цифрового фильтра [1, 2] имеет вид

из которого видно, что формирование массива отсчетов выходного сигнала происходит последовательно, причем длина и входного и выходного сигнала не ограничена. Таким образом, данный способ фильтрации в равной степени пригоден как для обработки записанных аудиосигналов, так и для потокового аудио. Два массива коэффициентов фильтра ({ar} и {bv}) полностью определяют характеристики фильтра. Заметим, что все стандартные задачи фильтрации аудиоконтента в Python можно решить вызовом функций и методов, соответствующих алгоритму РЦФ, используя библиотечные функции и методы [3-5], при этом от разработчика программы не требуется реализовывать поэлементную работу со значениями массивов аудиоданных. К уравнению в форме (3.1) в Python прибегают только в случаях, когда хочется осуществить плавную перестройку свойств фильтра по мере обработки записи, например, чтобы создать эффект “перемещения” слушателя и/или источника звука в пространстве друг относительно друга. Задача расчета рекурсивного фильтра заключается в выборе так называемого аналогового фильтра-прототипа некоторого порядка, и вычислении коэффициентов {ar} и {bv}, при которых будет обеспечиваться желаемая частотная характеристика фильтра. Для расчета фильтров существуют разные методы, наиболее простым из которых является метод обобщенного билинейного преобразования передаточной функции аналогового фильтра-прототипа, который и реализован в соответствующих стандартных функциях и методах Python. Фильтры-прототипы бывают разных семейств (Баттерворта, Чебышева, и т. п.) и могут быть разных порядков. Чем выше порядок фильтра-прототипа, тем резче будет выражен переход от полосы пропускания к полосе подавления на частотной характеристике итогового РЦФ, но при этом увеличивается объем вычислений и возникает ряд дополнительных нюансов.

Ход работы:

Была разработана программа для обработки аудиосигнала, его фильтрации и визуализации спектральных характеристик (Листинг 1). В качестве входного сигнала выбран рёв тигра, загруженый с ресурса Zvukogram [6].

Для загрузки аудиофайла используется библиотека librosa, позволяющая сохранить исходную частоту дискретизации. После загрузки определяется длина сигнала, создается временная шкала с помощью np.linspace, а спектральный анализ входного сигнала осуществляется через дискретное преобразование Фурье (np.fft.fft). Амплитудный спектр представляется в логарифмическом масштабе (дБ).

Фильтрация производится с помощью полосового фильтра Баттерворта (signal.butter) в диапазоне 100–250 Гц с коэффициентом усиления 3.0. Фильтр применяется к сигналу через signal.sosfilt, а усиление учитывается путем добавления отфильтрованного сигнала к исходному с соответствующим коэффициентом.

После фильтрации программа строит спектры входного и выходного сигналов в логарифмическом масштабе с применением matplotlib, используя логарифмическую шкалу для частоты. Временные представления сигналов также отображаются на графиках.

Обработанный сигнал сохраняется в выходной файл output.mp3 с помощью библиотеки soundfile.

Дополнительно программа выполняет кратковременное преобразование Фурье (STFT) для входного и выходного сигналов, используя гауссовое окно (gaussian) и библиотеку ShortTimeFFT. Спектрограммы визуализируются с логарифмическим масштабом по частоте и автоматическим масштабированием шкалы амплитуды.

Листинг 1 – Программа для загрузки сигнала, применения фильтра и построения графиков

import numpy as np

import matplotlib.pyplot as plt

import librosa

import soundfile as sf

from scipy.signal import ShortTimeFFT

from scipy.signal.windows import gaussian

from scipy import signal

plt.close("all") # Очистка памяти

# Загрузка данных звукового файла - стерео

input_signal, Fd = librosa.load("input.wav", sr=None, mono=False)

# Получить длину данных аудиофайла

N = len(np.transpose(input_signal))

T = round(N / Fd)

t = np.linspace(0, T, N)

# вычисляем спектр входного сигнала

Spectr_input = np.fft.fft(input_signal)

# Преобразуем в дБ:

AS_input = np.abs(Spectr_input)

eps = np.max(AS_input) * 1.0e-9

S_dB_input = 20 * np.log10(AS_input + eps)

# ------------------------------------------------------------

# Задаем граничные частоты полосы пропускания фильтра,в Герцах

lower_frequency = 100

upper_frequency = 250

gain = 3.0 # усиление в 3 раза согласно заданию

# типы фильтров: ‘lowpass’, ‘highpass’, ‘bandpass’, ‘bandstop’

# здесь bandpass. Ключ sos означает расчет в каскадной форме

order = 1 # порядок фильтра-прототипа

sos = signal.butter(order,

Wn=(lower_frequency / (Fd/2),

upper_frequency / (Fd/2)),

btype='bandpass', output='sos')

# а теперь собственно, фильтрация:

output_signal1 = signal.sosfilt(sos, input_signal)

K1 = gain # чтобы увеличить усиление в диапазоне втрое

output_signal = input_signal + (K1-1) * output_signal1

# Графики

# Расчет частотной хар-ки по коэф-ам фильтра

f, H1 = (signal.sosfreqz(sos, worN=Fd, whole=False, fs=Fd))

# комплексная частотная характеристика всего фильтра:

H = 1 + (K1-1)*H1

eps = 1e-10 # чтобы избежать lg(0)

L = 20 * np.log10(abs(H)+eps) # перевод в дБ

# Построим график АЧХ фильтра:

plt.semilogx(f, L)

plt.title('Digital filter frequency response')

plt.xlabel('Frequency [Hz]')

plt.ylabel('Level [dB]')

plt.xlim(10, Fd/2) # limit x axis

plt.ylim(-20, 20) # уменьшим нижний лимит по очевидной причине

plt.margins(0, 0.1)

plt.grid(which='both', axis='both')

plt.show()

# спектры до и после фильтрации

Spectr_output_real = np.fft.fft(output_signal)

S_dB_output_real = 20 * np.log10(np.abs(Spectr_output_real + eps))

f = np.arange(0, Fd / 2, Fd / N) # Перевести Абсциссу в Гц

S_dB_output_real = S_dB_output_real[:, : len(f)]

S_dB_input = S_dB_input[:, : len(f)]

plt.figure(figsize=(8, 3))

plt.semilogx(f, S_dB_input[0, :], color="b", label=r"input spectrum")

plt.semilogx(f, S_dB_output_real[0, :], color="r",alpha=0.7, label=r"output spectrum")

plt.grid(True)

plt.minorticks_on() # отобразит мелкую сетку на лог.масштабе

plt.grid(True, which="major", color="#444", linewidth=1)

plt.grid(True, which="minor", color="#aaa", ls=":")

# делаем красивый автомасштаб на оси ординат:

Max_A = np.max((np.max(np.abs(Spectr_input)),

np.max(np.abs(Spectr_output_real))))

Max_dB = np.ceil(np.log10(Max_A)) * 20

plt.axis([10, Fd / 2, Max_dB - 120, Max_dB])

plt.xlabel("Frequency (Hz)")

plt.ylabel("Level (dB)")

plt.title("Amplitude Spectrums of input and output audio")

plt.legend()

plt.show()

# Выводим график исходного и выходного аудиосигнала на одном графике

plt.figure(figsize=(8, 4))

plt.plot(t, input_signal[0, :], color="b", label="Input Signal")

plt.plot(t, output_signal[0, :], color="r", label="Output Signal", alpha=0.7)

plt.xlim([0, T])

plt.xlabel("Time (s)")

plt.ylabel("Amplitude")

plt.title("Входной и выходной сигналы")

plt.legend()

plt.grid(True)

plt.show()

# Записываем новый аудиофайл

sf.write("output.mp3", np.transpose(output_signal), Fd)

# Создаем фигуру с двумя субплотами рядом:

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))

# Общие параметры:

g_std = 0.2 * Fd

wind = gaussian(round(2 * g_std), std=g_std, sym=True)

hop = round(0.1 * Fd)

epss = 1e-6

# Настройки для входного сигнала:

SFT_in = ShortTimeFFT(wind, hop=hop, fs=Fd, scale_to='magnitude')

Sx_in = SFT_in.stft(input_signal[0, :])

# Настройки для выходного сигнала:

SFT_out = ShortTimeFFT(wind, hop=hop, fs=Fd, scale_to='magnitude')

Sx_out = SFT_out.stft(output_signal[0, :])

# Настройки общего отображения:

for ax, Sx, SFT, title in zip([ax1, ax2], [Sx_in, Sx_out], [SFT_in, SFT_out],

["Входной сигнал", "Выходной сигнал"]):

t_lo, t_hi = SFT.extent(N)[:2]

im = ax.imshow(20 * np.log10(abs(Sx) + epss),

origin='lower', aspect='auto',

extent=SFT.extent(N), cmap='viridis')

fig.colorbar(im, ax=ax, label="Magnitude $|S_x(t, f)|, dB $")

ax.set_title(f"{title}\n({SFT.m_num * SFT.T:g} s Gauss window, "

rf"$\sigma_t={g_std * SFT.T}\,$s)")

ax.set(xlabel=f"Time $t$ in seconds ({SFT.p_num(N)} slices, "

rf"$\Delta t = {SFT.delta_t:g}\,$s)",

ylabel=f"Freq. $f$ in Hz ({SFT.f_pts} bins, "

rf"$\Delta f = {SFT.delta_f:g}\,$Hz)",

xlim=(t_lo, t_hi))

ax.semilogy()

ax.set_xlim([0, T])

ax.set_ylim([10, Fd / 2])

ax.grid(which='major', color='#bbbbbb', linewidth=0.5)

ax.grid(which='minor', color='#999999', linestyle=':', linewidth=0.5)

ax.minorticks_on()

plt.tight_layout() # Автоматическая регулировка расстояний между графиками

plt.show()

После применения фильтра сигнал стал громче, рёв стал чуть более “объёмным”, других заметных изменений на слух не выявлено. На рисунках 2 – 5 представлены графики АЧХ, амплитудных спектров, визуализация, спектрограммы входного и выхоного сигналов соответственно.

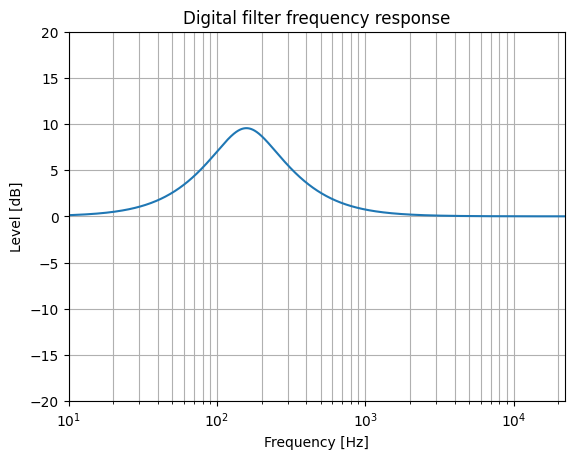
Рисунок 2 - Амплитудно-частотная характеристика фильтра

На графике АЧХ явно видно усиление в диапазоне 100-250 Гц.

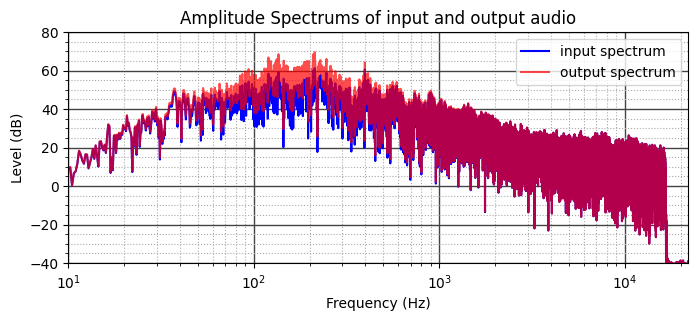
Рисунок 3 - График амплитудных спектров входного и выходного сигналов

На графике амплитудных спектров четко видно усиление частот выбранного диапазона (100 – 250 Гц). Также наблюдается усиление на прилежащих частотах, весь диапазон цсиления составил примерно от 20 до 1000 Гц.

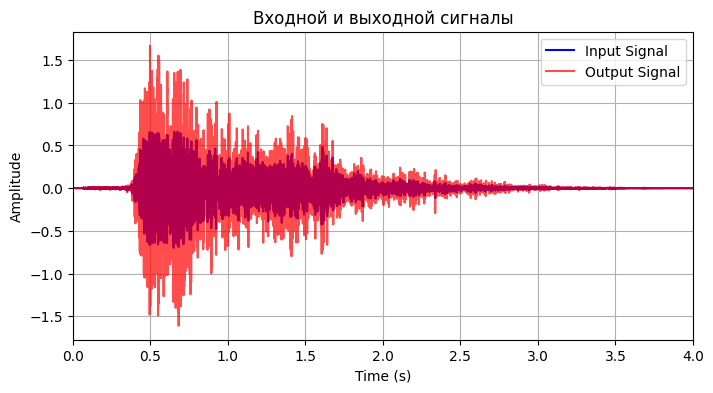
Рисунок 4 - Визуализация входного и выходного сигналов

На графике видно общее усиление сигнала.

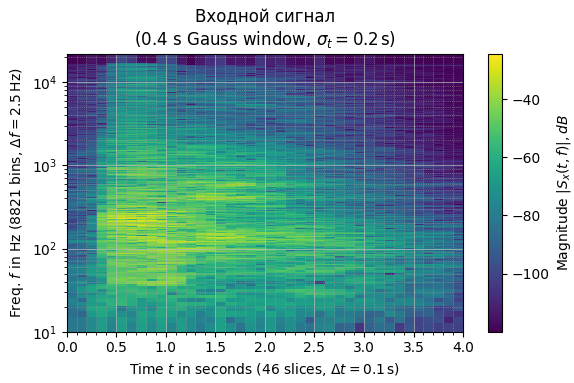
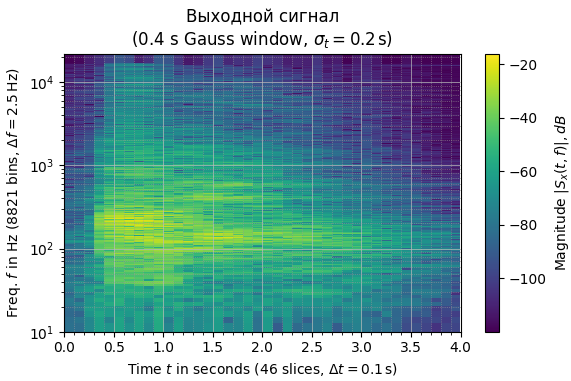
Рисунок 5 – Спектрграммы входного и выходного сигналов

Спектрограммы входного и выходного сигналов имеют незначительные отличия.

Получившийся выходной сигнал громче входного, имеет более “объёмный” звук, в отличии от полученного в предыдущей работе, который стал менее чётким, превратился в гул, в сравнении с входым сигналом.

Вывод: в ходе выполнения лабораторной работы были изучены основы обработки аудиосигналов на примере метода фильтрации сигналов во временной области с использованием рекурсивных цифровых фильтров. Разработана программа для применения фильтра и построения графиков. Фильтр успешно применён, выходной сигнал значительно отличается от полученного в предыдущей лабораторной работе.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. Жаринов О.О. Учебно-методические материалы к выполнению лабораторной работы №3 по дисциплине “Мультимедиа-технологии “. гр.4116,4117, 4118. ГУАП, 2025. – 16 с. (Интернет-ресурс) // URL: https://pro.guap.ru/inside/student/tasks/b1fa70870be81431ddf23edecfab3808/download

2. Методы и алгоритмы обработки звуковых сигналов. Курс лекций/ Э.И. Вологдин, СПб: 2012. – 96 с.

3. Аудиотехника. Учебник для вузов. / Ю.А. Ковалгин, Э.И. Вологдин – М.: Горячая линия-Телеком, 2013. – 742 с.

4. Алгоритм цифровой фильтрации в частотной и временной областях. // URL: http://stu.sernam.ru/book_g_rts.php?id=137

5. Рекурсивные цифровые фильтры. Материал из Национальной библиотеки им. Н.Э. Баумана. // URL: https://ru.bmstu.wiki/Рекурсивные_цифровые_фильтры

6. Zvukogram. База звуковых эффектов для монтажа. // URL: https://zvukogram.com/category/

7. SciPy API. Signal Processing (scipy.signal) .butter // URL: https://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.but ter.html

8. SciPy API. Signal processing (scipy.signal). # Matlab-style IIR filter design // URL: https://docs.scipy.org/doc/scipy/reference/signal.html