МТ2

ГУАП

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

доцент, канд. техн. наук, доцент				О.О. Жаринов
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №2

Основы обработки аудиосигналов средствами Python. Метод фильтрации в спектральном пространстве

по курсу: МУЛЬТИМЕДИА ТЕХНОЛОГИИ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ гр. №
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2025

Цель работы: Изучить основы обработки аудиосигналов на примере метода фильтрации сигналов в спектральном пространстве.

Вариант 13:

Рисунок 1 – Вариант задания на моделирование аудиосигнала

Краткие теоретические сведения о задачах обработки аудиосигналов и их практическом применении, а также о методах фильтрации:

Фильтрация является одним из широко применяемых методов обработки сигналов вообще и аудиосигналов в частности. К методам фильтрации часто прибегают, когда есть основания полагать, что в аудиозаписи имеется несколько источников звука, и хочется подчеркнуть или ослабить звучание одного из них. Кроме того, посредством фильтрации можно достичь эффектов, имитирующих звучание, характерное для записи звука в различных замкнутых помещениях, а также, наоборот, попытаться компенсировать нежелательную неравномерность частотной характеристики примененных ранее средств записи аудиосигнала. Методологической основой фильтрации является тот факт, что любая функция (а оцифрованный звук представляет собой набор последовательных значений некоторой неизвестной сложной функции) может быть представлена суммой множества гармонических компонентов с различными частотами и фазами. Всевозможные аудиосигналы любой природы содержат в себе в различных сочетаниях колебания с частотами от 20 Гц до 20 кГц.

Компоненты человеческого голоса можно условно разделить на три диапазона, согласно входящим в них звукам: взрывным, гласным и шипящим. Взрывные звуки лежат в диапазоне от 125 Гц до 250 Гц и "отвечают" за разборчивость речи, так как именно они позволяют нам определить, кто именно говорит. На долю гласных, которые лежат в диапазоне от 350 Гц до 2000 Гц, приходится максимальное количество голосовой энергии. Шипящие в диапазоне от 1500 Гц до 4000 Гц несут сравнительно мало энергии, однако от них зависит четкость и разборчивость речи. Частотный диапазон от 63 Гц до 500 Гц содержит около 60% всей энергии голоса, однако на его долю приходится лишь 5% информационного наполнения речи. Диапазон от 500 Гц до 1 кГц содержит около 35% информации, а остальные 60% информационного наполнения приходятся на долю "шипящего" диапазона от 1 кГц до 8 кГц, который несет лишь 5% энергии.

Для получения информации о частотном составе любых сигналов в дискретном времени существует специальный метод и алгоритм – быстрое преобразование Фурье (БПФ). В результате его применения к массиву {xn}, который представляет собой, например, последовательность оцифрованных значений звука, образуется массив значений спектра {Xn}. Значения спектра являются комплексными числами, а модуль каждого из них пропорционален амплитуде гармонического компонента, содержащегося в обрабатываемой записи аудисосигнала. Связь целочисленного индекса элементов массива {Xn} с частотой дается формулой

где TД – период дискретизации сигнала.

Существует также и алгоритм обратного действия (обратное БПФ): по массиву значений спектра {Xn} можно вычислить массив значений сигнала {xn} (иногда говорят “восстановить сигнал из его спектра”).

Идея метода фильтрации в спектральном пространстве (который также известен под названием “метод Фурье-фильтрации”) заключается в том, чтобы каким-то образом изменить спектр исходного сигнала и восстановить аудиосигнал из измененного спектра.

Таким образом, метод фильтрации реализуется в три шага:

1) производится вычисление спектра {Xn} исходного аудиосигнала {xn},

2) осуществляется изменение некоторого количества значений спектра {Xn} в соответствии желаемыми частотными свойствами фильтра, в результате чего получается измененный спектр {Yn},

3) выполняется формировании выходного аудиосигнала посредством вычисления обратного преобразования Фурье спектра {Yn}.

Процедура изменения спектра исходного сигнала при реализации методов линейной фильтрации реализуется как поэлементное умножение двух массивов: исходного спектра {Xn} и предварительно сформированного массива значений передаточной функции фильтра {Wn}:

При задании массива {Wn} исходят из требований к типу фильтрации. Например, если необходимо оставить без изменения частотные компоненты аудиосигнала в определенном диапазоне частот и максимально ослабить остальные компоненты, то используется следующий подход:

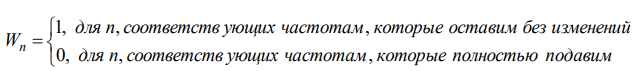
При реализации цифровых эквалайзеров можно задавать желаемый коэффициент пропускания, отличный от нуля, для разных частотных диапазонов, можно даже задавать функциональную зависимость желаемого коэффициента пропускания от частоты.

На практике, например, при обработке не очень качественных записей речевых сигналов бывает полезно несколько уменьшить уровень сигнала в области низких частот и "поднять" в диапазоне 1..5 кГц, что заметно улучшает субъективно воспринимаемую четкость и разборчивость речи. Подъем частотной характеристики в области 100..250 Гц делает звучание вокальных партий в музыкальных произведениях гулким и "грудным". Вырезание частотного диапазона 150..500 Гц приводит к тому, что голос начинает звучать "как в трубе". "Провалы" отдельных участков в диапазоне 500..1000 Гц делают голос жестче, а подъемы в области 1 кГц и 3 кГц придают вокалу металлический "носовой" оттенок. Вырезание участков в диапазоне 2..5 кГц делает голос вялым, безжизненным и неразборчивым, а усиление частот 4..10 кГц приводит к появлению яркости и "искристости”.

При программной реализации метода фильтрации в спектральном пространстве нужно обязательно выполнять требование комплексносопряженной симметрии [3,4] для задаваемого массива {Wn}:

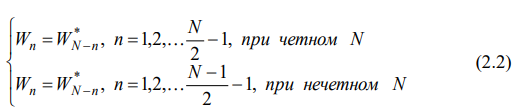
где * означает операцию комплексного сопряжения (другими словами, если, например, W2=0.5+j∙0.5, то нужно выполнить WN−2=0.5−j∙0.5), чтобы свойство комплексно-сопряженной симметрии сохранялось у спектра выходного сигнала. При этом значение W0 должно быть обязательно вещественным, также и WN/2 при четном N должно быть вещественным.

Ход работы:

Была разработана программа для обработки аудиосигнала, его фильтрации и визуализации спектральных характеристик (Листинг 1). В качестве входного сигнала был выбран рёв тигра.

Для загрузки аудиофайла использовалась библиотека librosa, которая позволяет загружать стерео-сигналы с сохранением частоты дискретизации. После загрузки определяется длина сигнала, и создается временная шкала с помощью np.linspace. Спектральный анализ входного сигнала осуществляется через дискретное преобразование Фурье (np.fft.fft), а амплитудный спектр представляется в логарифмическом масштабе (дБ).

Фильтрация производится путем создания передаточной функции полосового фильтра, определяемой в диапазоне 100–250 Гц с коэффициентом усиления 3.0. Для этого границы фильтра переводятся в индексы массива спектра, а затем амплитудный спектр входного сигнала умножается на передаточную функцию. Обратное преобразование Фурье (np.fft.ifft) позволяет получить отфильтрованный сигнал.

После фильтрации программа строит спектры входного и выходного сигналов в логарифмическом масштабе, а также временные представления сигналов. Для визуализации используется matplotlib, при этом применяется логарифмическая шкала для частоты и автоматическое масштабирование оси амплитуды.

Обработанный сигнал сохраняется в выходной файл output.mp3 с использованием библиотеки soundfile.

Дополнительно программа выполняет кратковременное преобразование Фурье (STFT) для входного и выходного сигналов с использованием гауссового окна и последующей визуализацией спектрограмм. В качестве окна используется функция gaussian, а для вычислений применяется ShortTimeFFT.

Листинг 1 – Программа для загрузки сигнала, его обработки и построения графиков

import numpy as np

import matplotlib.pyplot as plt

import librosa

import soundfile as sf

from scipy.signal import ShortTimeFFT

from scipy.signal.windows import gaussian

plt.close("all")  # Очистка памяти

# Загрузка данных звукового файла - стерео

input_signal, Fd = librosa.load("input.wav", sr=None, mono=False)

# Получить длину данных аудиофайла

N = len(np.transpose(input_signal))

T = round(N / Fd)

t = np.linspace(0, T, N)

# вычисляем спектр входного сигнала

Spectr_input = np.fft.fft(input_signal)

# Преобразуем в дБ:

AS_input = np.abs(Spectr_input)

eps = np.max(AS_input) * 1.0e-9

S_dB_input = 20 * np.log10(AS_input + eps)

# Задаем граничные частоты полосы пропускания фильтра, в Герцах

lower_frequency = 100

upper_frequency = 250

gain = 3.0 # усиление в 3 раза согласно заданию

# Переводим Герцы в целочисленные индексы массива:

n_dn = round(N * lower_frequency / Fd)

n_up = round(N * upper_frequency / Fd)

# Создаем массив значений передаточной функции фильтра:

W = np.zeros_like(Spectr_input)  # массив из нулей

# W = np.ones_like(Spectr_input) # массив из единиц

# W наполняем с учетом фоормулы (2.2) для полосового фильтра:

W[:, n_dn : n_up + 1] = gain  # первая половина

W[:, N - n_up : N - n_dn + 1] = gain  # 'зеркальная' половина

# Считаем массив значений спектра для выходного сигнала

Spectr_output = Spectr_input * W  # по формуле (2.1)

# Обратное БПФ от модифицированного спектра:

print(

    np.max(np.abs(np.imag(np.fft.ifft(Spectr_output))))

    / np.max(np.abs(np.real(np.fft.ifft(Spectr_output))))

)

output_signal = np.real(np.fft.ifft(Spectr_output))

# спектры до и после фильтрации

Spectr_output_real = np.fft.fft(output_signal)

S_dB_output_real = 20 * np.log10(np.abs(Spectr_output_real + eps))

f = np.arange(0, Fd / 2, Fd / N)  # Перевести Абсциссу в Гц

S_dB_output_real = S_dB_output_real[:, : len(f)]

S_dB_input = S_dB_input[:, : len(f)]

plt.figure(figsize=(8, 3))

plt.semilogx(f, S_dB_input[0, :], color="b", label=r"input spectrum")

plt.semilogx(f, S_dB_output_real[0, :], color="r", label=r"output spectrum")

plt.grid(True)

plt.minorticks_on()  # отобразит мелкую сетку на лог.масштабе

plt.grid(True, which="major", color="#444", linewidth=1)

plt.grid(True, which="minor", color="#aaa", ls=":")

# делаем красивый автомасштаб на оси ординат:

Max_A = np.max((np.max(np.abs(Spectr_input)), np.max(np.abs(Spectr_output_real))))

Max_dB = np.ceil(np.log10(Max_A)) * 20

plt.axis([10, Fd / 2, Max_dB - 120, Max_dB])

plt.xlabel("Frequency (Hz)")

plt.ylabel("Level (dB)")

plt.title("Amplitude Spectrums of input and output audio")

plt.legend()

plt.show()

# Выводим график исходного и выходного аудиосигнала на одном графике

plt.figure(figsize=(8, 4))

plt.plot(t, input_signal[0, :], color="b", label="Input Signal")

plt.plot(t, output_signal[0, :], color="r", label="Output Signal", alpha=0.7)

plt.xlim([0, T])

plt.xlabel("Time (s)")

plt.ylabel("Amplitude")

plt.title("Входной и выходной сигналы")

plt.legend()

plt.grid(True)

plt.show()

# Записываем новый аудиофайл

sf.write("output.mp3", np.transpose(output_signal), Fd)

# Создаем фигуру для спектрограмм:

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))

# Общие параметры:

g_std = 0.2 * Fd

wind = gaussian(round(2 * g_std), std=g_std, sym=True)

hop = round(0.1 * Fd)

epss = 1e-6

# Настройки для входного сигнала:

SFT_in = ShortTimeFFT(wind, hop=hop, fs=Fd, scale_to='magnitude')

Sx_in = SFT_in.stft(input_signal[0, :])

# Настройки для выходного сигнала:

SFT_out = ShortTimeFFT(wind, hop=hop, fs=Fd, scale_to='magnitude')

Sx_out = SFT_out.stft(output_signal[0, :])

# Настройки общего отображения:

for ax, Sx, SFT, title in zip([ax1, ax2], [Sx_in, Sx_out], [SFT_in, SFT_out],

                             ["Входной сигнал", "Выходной сигнал"]):

    t_lo, t_hi = SFT.extent(N)[:2]

   

    im = ax.imshow(20 * np.log10(abs(Sx) + epss),

                   origin='lower', aspect='auto',

                   extent=SFT.extent(N), cmap='viridis')

    fig.colorbar(im, ax=ax, label="Magnitude $|S_x(t, f)|, dB $")

   

    ax.set_title(f"{title}\n({SFT.m_num * SFT.T:g} s Gauss window, "

                 rf"$\sigma_t={g_std * SFT.T}\,$s)")

    ax.set(xlabel=f"Time $t$ in seconds ({SFT.p_num(N)} slices, "

           rf"$\Delta t = {SFT.delta_t:g}\,$s)",

           ylabel=f"Freq. $f$ in Hz ({SFT.f_pts} bins, "

           rf"$\Delta f = {SFT.delta_f:g}\,$Hz)",

           xlim=(t_lo, t_hi))

   

    ax.semilogy()

    ax.set_xlim([0, T])

    ax.set_ylim([10, Fd / 2])

    ax.grid(which='major', color='#bbbbbb', linewidth=0.5)

    ax.grid(which='minor', color='#999999', linestyle=':', linewidth=0.5)

    ax.minorticks_on()

plt.tight_layout()  # Автоматическая регулировка расстояний между графиками

plt.show()

После применения фильтра рёв тигра “превратился” в гул, как будто звук был воспроизведен под водой. На рисунках 1 – 3 представлены графики амплитудных спектров, визуализация, спектрограммы входного и выхоного сигналов соответственно.

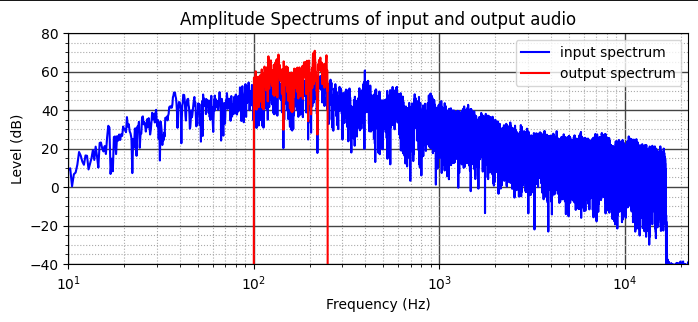
Рисунок 1 - График амплитудных спектров входного и выходного сигналов

На графике амплитудных спектров четко видно усиление частот выбранного диапазона (100 – 250 Гц).

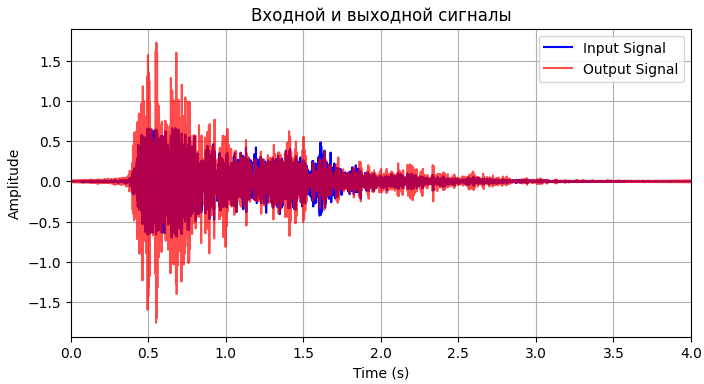
Рисунок 2 - Визуализация входного и выходного сигналов

На графике видно общее усиление сигнала, лишь на некоторых участках входной сигнал был подавлен.

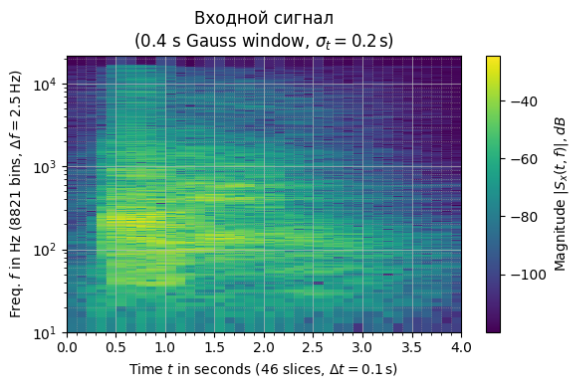
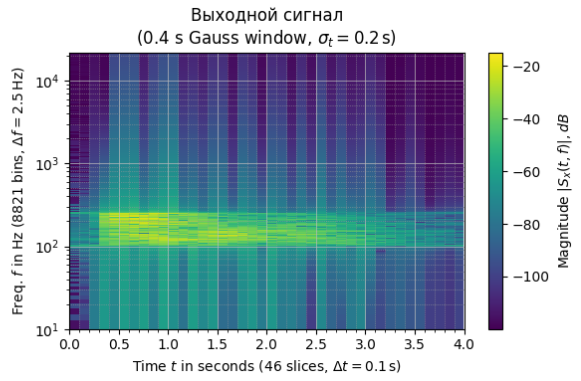
Рисунок 3 – Спектрграммы входного и выходного сигналов

По спектрограммам также явно заметно усиление сигнала в выбранном диапазоне. Графики отобразили корректное и успешно применение фильтра.

Вывод: в ходе выполнения лабораторной работы были изучены основы обработки аудиосигналов на примере метода фильтрации сигналов в спектральном пространстве. Разработана и успешно выполнена программа для применения фильтра согласно варианту задания и построения графиков.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. Жаринов О.О. Учебно-методические материалы к выполнению лабораторной работы №2 по дисциплине “Мультимедиа-технологии “. гр.4116,4117, 4118, Z0411. ГУАП, 2025. – 17 с. (Интернет-ресурс) // URL: https://pro.guap.ru/inside/student/tasks/ebc6a2127311e8d70f17dd5a3b0c85e3/download

2. Методы и алгоритмы обработки звуковых сигналов. Курс лекций/ Э.И. Вологдин, СПб: 2012. – 96 с.

3. Аудиотехника. Учебник для вузов. / Ю.А. Ковалгин, Э.И. Вологдин – М.: Горячая линия-Телеком, 2013. – 742 с.

4. Алгоритм цифровой фильтрации в частотной и временной областях. // URL: http://stu.sernam.ru/book_g_rts.php?id=137

5. Фильтрация сигнала в частотной области - Цифровая обработка сигналов. // URL: http://www.cyberforum.ru/digital-signalprocessing/thread1663620.html

6. Zvukogram. База звуковых эффектов для монтажа. // URL: https://zvukogram.com/category/