МТ1

ГУАП

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

доцент, канд. техн. наук, доцент				О.О. Жаринов
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №1

Основы моделирования и обработки аудиосигналов средствами Python

по курсу: МУЛЬТИМЕДИА ТЕХНОЛОГИИ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ гр. №
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2025

Цель работы: Получить представление о принципах формирования аудиосигналов и приобрести навыки обработки звуковых файлов с использованием средств Python.

Вариант 13:

Рисунок 1 – Вариант задания на моделирование аудиосигнала

Ход работы:

Оцифрованный звук сохраняют в файлах, данные в котором представлены в одном из стандартных форматов кодирования звука. В ходе данной лабораторной рабоыт для работы с аудиоконтентом был использован язык программирования Python и библиотеки numpy, librosa, scipy, soundfile.

Была разработана программа для моделирования сигнала с заданными по варианту характеристиками и записи его в файл (Листинг 1). Для вычислений использовалась библиотека NumPy. В частности, применен метод np.arange для создания массива индексов, который затем преобразуется в временные отсчеты через деление на частоту дискретизации. Для генерации модулирующих сигналов (синусоидального и косинусоидального) использовалась функция np.sin и np.cos с заданной частотой модуляции. Несущий сигнал, представляющий собой синусоиду с частотой 3000 Гц, также создается с помощью np.sin. Далее амплитудная модуляция происходит путем умножения модулирующих сигналов на несущий, создавая два канала: левый и правый.

Листинг 1 – Моделирование и запись сигнала

import numpy as np

import soundfile as sf

Fd = 44100  # Частота дискретизации

T = 3       # Длительность в секундах

N = round(T * Fd)

# Частота несущего сигнала

f_carrier = 3000  # 3000 Гц

# Частота модуляции амплитуды

f_mod = 1  # 1 Гц

def generate_signal(f_carrier, f_mod, N, Fd):

    t = np.arange(N) / Fd

   

    # Модулирующие сигналы:

    mod_left = np.sin(2 * np.pi * f_mod * t)  # Синус для левого канала

    mod_right = np.cos(2 * np.pi * f_mod * t) # Косинус для правого

   

    # Несущий сигнал:

    carrier = np.sin(2 * np.pi * f_carrier * t)

   

    # Модулируем амплитуду:

    left_channel = mod_left * carrier  # Левый канал: sin(1Hz) * sin(3000Hz)

    right_channel = mod_right * carrier # Правый канал: cos(1Hz) * sin(3000Hz)

   

    return np.vstack((left_channel, right_channel))

# Генерируем сигнал

model_signal = generate_signal(f_carrier, f_mod, N, Fd)

# Нормировка

Norm = np.max(np.abs(model_signal))

if Norm != 0:

    model_signal = model_signal / Norm

# Запись в файл

sf.write('C:/Custom/Study/8sem/MT/1/output2.wav', np.transpose(model_signal), Fd)

В Листинге 2 представлена программа для чтения аудиофайла. Сначала аудиофайл загружается с помощью функции sf.read, которая возвращает сам сигнал и его частоту дискретизации. Затем сигнал транспонируется, чтобы правильно разделить каналы, если аудиофайл стерео. После этого вычисляются параметры сигнала: количество каналов (1 для моно и 2 для стерео), общее количество отсчетов и продолжительность сигнала в секундах. Эти данные позволяют дальше анализировать характеристики аудиофайла. В коде также выводится информация о типе данных сигнала, количестве каналов, общей длительности и частоте дискретизации для удобства дальнейшей обработки (Рисунок 1).

Листинг 2 – Чтение аудиофайла

import soundfile as sf

input_signal, Fd = sf.read('C:/Custom/Study/8sem/MT/1/output2.wav')

input_signal=input_signal.T

K = len(input_signal) # если стерео, то 2, если моно - 1

N = input_signal.size # количество дискретных отсчетов звука

T = N/Fd/K # время звучания в секундах

print(type(input_signal), K, N, Fd, T)

Рисунок 1 – Параметры аудиофайла

На рисунке видно, что считанный файл представляет собой массив формата <class ‘numpy.ndarray’>, 2 канала, 264600 дискретных отсчетов (2 канала по 3 секунды с частотой дискретизации 44100), длительность 3 секунды.

В листинге 3 представлен код для визуализации аудиосигнала с использованием библиотеки Matplotlib для построения графиков и Librosa для отображения волновых форм (Рисунок 2). Для этого заданы временные границы для двух различных визуализаций: первая от 0 до 0.01 секунды, а вторая от 0 до 3 секунд. Для каждой визуализации создается отдельная фигура с помощью plt.subplots с одним графиком, на котором отображаются две волновые формы — для левого и правого канала. Для каждого канала используется метод librosa.display.waveshow, который отображает аудиосигнал с заданной частотой дискретизации.

Листинг 3 – Визуализация аудиосигнала

import numpy as np

import librosa.display

start_t, stop_t = 0, 0.01 # границы по времени для визуализации

fig, ax = plt.subplots(nrows=1, sharex=True, figsize=(10, 4))

ax.set(xlim=[start_t, stop_t])

librosa.display.waveshow(input_signal[0, :],

    sr=Fd, color='b', ax=ax,

    label='left channel')

librosa.display.waveshow(input_signal[1, :],

    sr=Fd, color='r', ax=ax,

    label='right channel')

ax.label_outer()

ax.legend()

ax.grid()

plt.xlabel('Time')

plt.ylabel('Amplitude')

plt.title('Audio Signal')

plt.show()

start_t, stop_t = 0, 3 # границы по времени для визуализации

fig, ax = plt.subplots(nrows=1, sharex=True, figsize=(10, 4))

ax.set(xlim=[start_t, stop_t])

librosa.display.waveshow(input_signal[0, :],

    sr=Fd, color='b', ax=ax, alpha=0.4,

    label='left channel')

librosa.display.waveshow(input_signal[1, :],

    sr=Fd, color='r', ax=ax, alpha=0.4,

    label='right channel')

ax.label_outer()

ax.legend()

ax.grid()

plt.xlabel('Time')

plt.ylabel('Amplitude')

plt.title('Audio Signal')

plt.show()

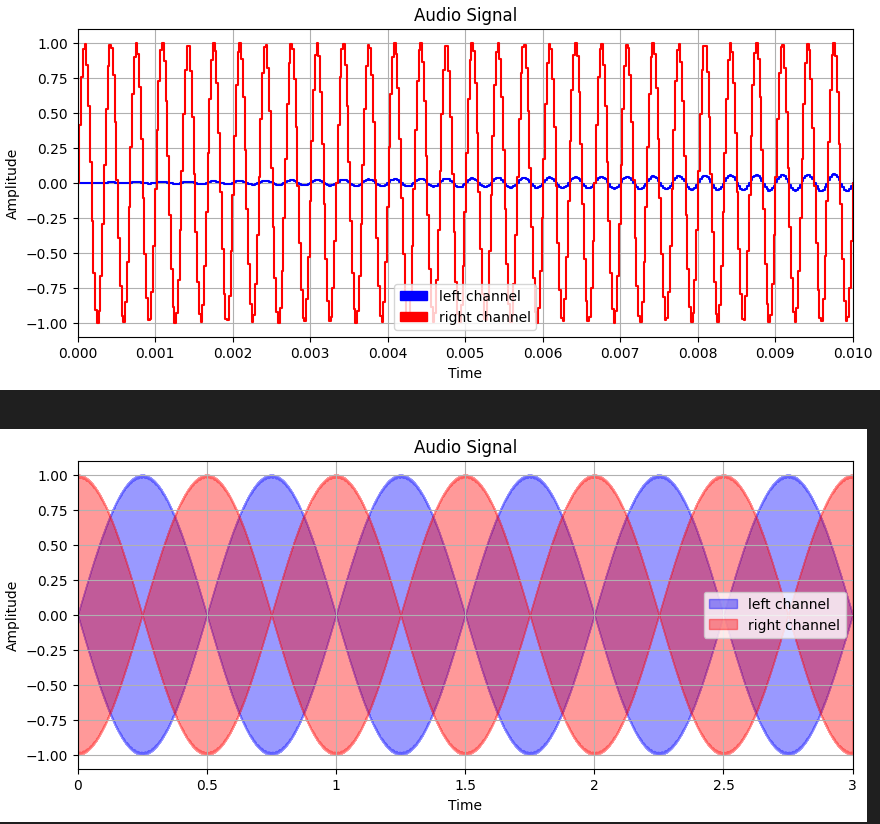
Рисунок 2 – Визуализация аудиосигнала

Левый канал (синий цвет) модулируется синусоидально, а правый канал (красный цвет) — косинусоидально.

В листинге 4 представлен код для построения графиков амплитудного спектра правого и левого каналов. Для анализа были рассчитаны амплитудные спектры для левого и правого каналов с помощью функции np.fft.fft, которая выполняет быстрое преобразование Фурье. Далее, с помощью функции np.fft.fftfreq, были получены частоты, соответствующие спектру сигнала в диапазоне от 0 до половины частоты дискретизации Fd/2, так как спектр является симметричным. Затем амплитудные спектры были преобразованы в децибелы с помощью функции to_db, которая учитывает возможные малые значения с добавлением малого числа для предотвращения ошибки логарифмирования нуля. Для визуализации амплитудных спектров были созданы два графика, каждый для одного канала, с использованием метода plot. Гграфики были построены в логарифмическом масштабе по оси частоты с диапазоном от 2900 до 3100 Гц и уровнем амплитуды от -60 до 5 дБ (Рисунок 3).

Листинг 4 – Визуализация амплитудного спектра

import numpy as np

import matplotlib.pyplot as plt

# Вычисляем амплитудные спектры для обоих каналов:

Spectr_left = np.fft.fft(input_signal[0, :])

Spectr_right = np.fft.fft(input_signal[1, :])

N = len(input_signal[0, :])

freq = np.fft.fftfreq(N, 1/Fd)[:N//2]

# Преобразуем в дБ:

def to_db(spectrum):

    eps = 1e-9  # Фиксированное значение для избежания log(0)

    return 20 * np.log10(np.abs(spectrum[:N//2]) + eps)

S_dB_left = to_db(Spectr_left)

S_dB_right = to_db(Spectr_right)

# Создаем два отдельных графика:

fig, (ax1, ax2) = plt.subplots(nrows=2, figsize=(12, 8), sharex=True)

# Левый канал:

ax1.plot(freq, S_dB_left, color='blue', label='Левый канал (модуляция: sin)')

ax1.set_title('Амплитудный спектр: левый канал')

ax1.set_ylabel('Уровень (дБ)')

ax1.grid(ls=':', alpha=0.5)

ax1.legend()

ax1.set_xscale('log')  # Логарифмический масштаб по X

ax1.set_xlim(2900, 3100)  

ax1.set_ylim(-60, 5)

# Правый канал:

ax2.plot(freq, S_dB_right, color='red', label='Правый канал (модуляция: cos)')

ax2.set_title('Амплитудный спектр: правый канал')

ax2.set_xlabel('Частота (Гц)')

ax2.set_ylabel('Уровень (дБ)')

ax2.grid(ls=':', alpha=0.5)

ax2.legend()

ax2.set_xscale('log')  # Логарифмический масштаб по X

# Настраиваем отображение сетки для логарифмической оси

for ax in (ax1, ax2):

    ax.grid(True, which='both', ls=':', alpha=0.5)

plt.tight_layout()

plt.show()

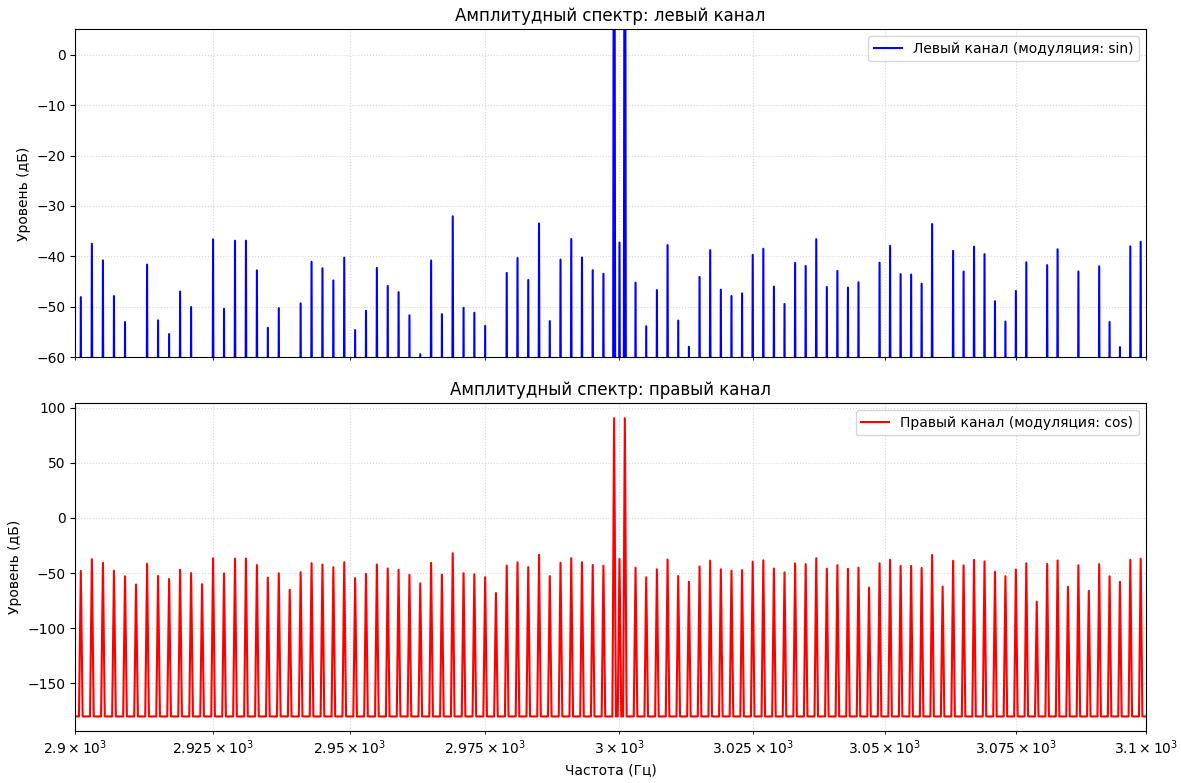
Рисунок 3 – Амплитудные спектры каналов

Оба графика демонстрируют характерную для амплитудной модуляции структуру спектра с центральной частотой и боковыми полосами, обусловленными модуляцией. 

В листинге 5 представлен код для построения спектрограмм. Для анализа использовалось коротковременное преобразование Фурье (STFT), реализованное с помощью функции ShortTimeFFT. Программа использует симметричное окно Гаусса с отклонением, равным 20% от частоты дискретизации Fd, и выполняет STFT с шагом 0.1 секунды, что позволяет получить временную и частотную структуру сигнала. Для построения графиков используется функция imshow, отображающая амплитуду сигнала, с добавлением сеток и меток осей для улучшения восприятия. Первый график отображает амплитуду в линейной шкале, а второй преобразует амплитуду в децибелы для лучшей визуализации, так как первый получился не информативным. Оба графика используют логарифмическую шкалу частот (Рисунок 4).

Листинг 5 – Вычисление и визуализация спектрограмм

# Вычисляем и строим спектрограмму 1:

# standard deviation for Gauss. window (in samples!):

g_std = 0.2*Fd

# symmetric Gaussian window:

wind = gaussian(round(2*g_std), std=g_std, sym=True)

SFT = ShortTimeFFT(wind,

    hop=round(0.1*Fd), # прыгаем по 0.1 сек

    fs=Fd,

scale_to='magnitude')

Sx = SFT.stft(input_signal[0,:]) # perform the STFT

# далее только построение графика спектрограммы:

fig1, ax1 = plt.subplots(figsize=(6, 4))

t_lo, t_hi = SFT.extent(N)[:2] # time range of plot

# тут очень хитро сделанные надписи на осях, жаль чистить:

ax1.set_title(rf"STFT ({SFT.m_num*SFT.T:g}$\,s$ Gauss window,"+

     rf"$\sigma_t={g_std*SFT.T}\,$s)")

ax1.set(xlabel=f"Time $t$ in seconds ({SFT.p_num(N)} slices,"+

    rf"$\Delta t = {SFT.delta_t:g}\,$s)",

    ylabel=f"Freq. $f$ in Hz ({SFT.f_pts} bins, "+

    rf"$\Delta f = {SFT.delta_f:g}\,$Hz)",

    xlim=(t_lo, t_hi))

im1 = ax1.imshow(abs(Sx), origin='lower', aspect='auto',

    extent=SFT.extent(N), cmap='viridis')  

fig1.colorbar(im1, label="Magnitude $|S_x(t, f)|$")

ax1.semilogy()

ax1.set_xlim([0, T])

ax1.set_ylim([10, Fd/2])

# Show the major grid and style it slightly.

ax1.grid(which='major', color='#bbbbbb', linewidth=0.5)

# Show the minor grid as well.

# Style it in very light gray as a thin, dotted line.

ax1.grid(which='minor', color='#999999', linestyle=':',

linewidth=0.5)

# Make the minor ticks and gridlines show.

ax1.minorticks_on()

plt.show()

# строим спектрограмму 2:

fig1, ax1 = plt.subplots(figsize=(6, 4))

t_lo, t_hi = SFT.extent(N)[:2] # time range of plot

# тут очень хитро сделанные надписи на осях, жаль чистить:

ax1.set_title(rf"STFT ({SFT.m_num*SFT.T:g}$\,s$ Gauss window,"+

     rf"$\sigma_t={g_std*SFT.T}\,$s)")

ax1.set(xlabel=f"Time $t$ in seconds ({SFT.p_num(N)} slices,"+

    rf"$\Delta t = {SFT.delta_t:g}\,$s)",

    ylabel=f"Freq. $f$ in Hz ({SFT.f_pts} bins, "+

    rf"$\Delta f = {SFT.delta_f:g}\,$Hz)",

    xlim=(t_lo, t_hi))

epss=np.max(abs(Sx))*1e-6

im1 = ax1.imshow(20*np.log10(abs(Sx)+epss),

 origin='lower', aspect='auto',

 extent=SFT.extent(N), cmap='viridis')

fig1.colorbar(im1, label="Magnitude $|S_x(t, f)|, dB $")

ax1.semilogy()

ax1.set_xlim([0, T])

ax1.set_ylim([10, Fd/2])

# Show the major grid and style it slightly.

ax1.grid(which='major', color='#bbbbbb', linewidth=0.5)

# Show the minor grid as well.

# Style it in very light gray as a thin, dotted line.

ax1.grid(which='minor', color='#999999', linestyle=':',

linewidth=0.5)

# Make the minor ticks and gridlines show.

ax1.minorticks_on()

plt.show()

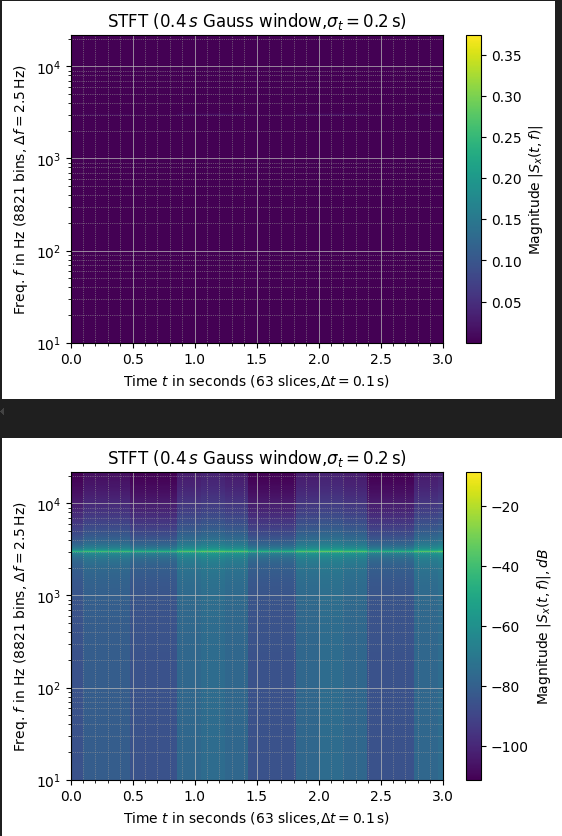
Рисунок 4 – Спектрограммы

  Первый график получился не информативным, на втором четко видна несущая частота 3000 Гц и изменения в амплитуде.

Вывод: в ходе выполнения лабораторной работы было получено представление о принципах формирования аудиосигналов и приобретены навыки обработки звуковых файлов с использованием средств Python. Удалось успешно смоделировать сигнал с синусоидальной модуляцией в левом канале и косинусоидальной в правом канале.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. 10 аудиомодулей Python для воспроизведения и записи // URL: https://pythonpip.ru/osnovy/10-audiomoduley-python-dlyavosproizvedeniya-i-zapisi

2. Audio Signal Processing with Python’s Librosa /E. Daehnhardt. 2023. // URL: https://daehnhardt.com/blog/2023/03/05/python-audio-signalprocessing-with-librosa/

3. SciPy.signal.ShortTimeFFT (документация на англ. яз.) // URL:

https://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.ShortTime

FFT.html#scipy.signal.ShortTimeFFT

4. Практическое применение преобразования Фурье для анализа

сигналов. Введение для начинающих. // URL: https://habr.com/ru/articles/269991/

5. Спектрограмма звука - как читать // URL: https://chistoug.ru/articles/spektrogramma-zvuka-kak-chitat.html