Домашка ВАР21

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

«Московский технический университет связи и информатики»

Кафедра "Техническая электродинамика и антенны"

Домашнее задание

По курсу Электродинамика и распространение радиоволн

"Электромагнитное поле в световоде"

Вариант 21

Выполнил:

студент группы

Проверила:

Москва 2024

Дано:

Задание 1.

Определить комплексные амплитуды всех проекций у векторов в средах 1 и 2 при .

Найдем :

Найдем производные. Производная комплексной амплитуды z-составляющей по координате x и x-составляющей по координате z в первой среде:

Комплексные амплитуды всех проекций:

Задание 2.

Составляются и совместно решаются уравнения, которые связывают между собой неизвестные поперечные волновые числа в средах 1 и 2, т.е. и .

Запишем уравнение Гельмгольца для первой среды:

где - оператор Гамильтона:

Где

По аналогии запишем уравнение Гельмгольца для второй среды:

Где

Сложив уравнения, получим:

Домножив на получим:

Где , и , тогда:

Рассмотрим применение граничных условий на границе раздела (при ):

Граничные условия при требуют равенства :

Граничные условия при требуют равенства :

Домножаем на :

Тогда заменяем , и получаем:

После всех расчетов и преобразований получим два уравнения:

Построив графики по полученным двум уравнениям, мы увидим, что мы имеем две точки пересечения, что свидетельствует о распространении двух типов волны в световоде.

Задание 3.

Определить минимальную и максимальную толщины световода, при которых по нему будет распространяться только волна низшего типа.

Из условия одноволнового режима (одна точка пересечения) , находим максимально возможную толщину :

Рисунок 1 – Решение трансцендентного уравнения при максимальном h

Из условия находим минимальную толщину , начиная с которой существует одноволновой режим:

Рисунок 2 – Решение трансцендентного уравнения при минимальном h

Найдём среднюю световода:

Тогда :

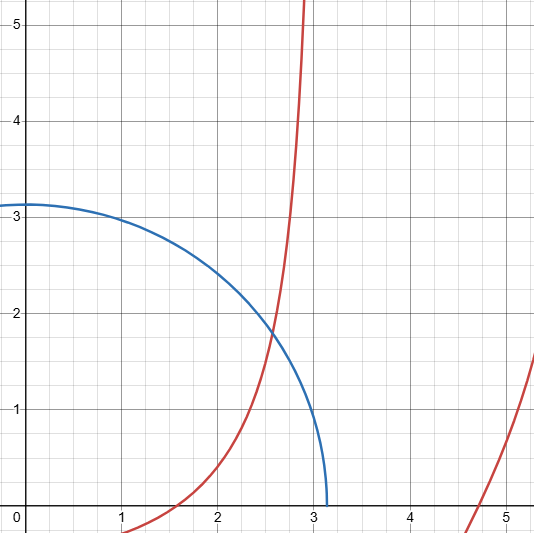
Рисунок 3 – Решение трансцендентного уравнения при среднем h

Задание 4.

Для средней толщины световода вычислить параметры волны низшего типа и .

Для толщины волновода трансцендентные уравнения принимают вид:

Получаем:

Определяем постоянные распространения волны в световоде:

Фазовая скорость волны в световоде находится по формуле:

Задание 5.

Определить амплитуды А и В, входящие в выражения для всех проекций векторов.

Для расчетов воспользуемся вектором Пойтинга. Комплексный вектор Пойнтинга определяется как половина векторного произведения комплексной амплитуды вектора напряжённости электрического поля на комплексно-сопряжённое комплексной амплитуды вектора напряжённости магнитного поля.

Для решения данной задачи понадобится только z-ая компонента вектора Пойнтига, перепишем:

Запишем выражение для :

Учтём, что , и что знак минуса указывает только на направление потока, тогда получим:

Отсюда можно выразить A:

Коэффициент B можно найти из граничных условий:

Задание 6.

Построить зависимости амплитуд всех проекций векторов и от координаты x в области и в области .