Ломашка ВАР6

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

“Московский технический университет связи и информатики”

(МТУСИ)

Кафедра "Техническая электродинамика и антенны"

Домашнее задание

по курсу Электродинамика и распространение радиоволн

"Электромагнитное поле в световоде"

Вариант 6

Выполнил:

Студент группы

Проверила:

Москва 2024

Дано:

,

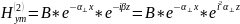
мВт

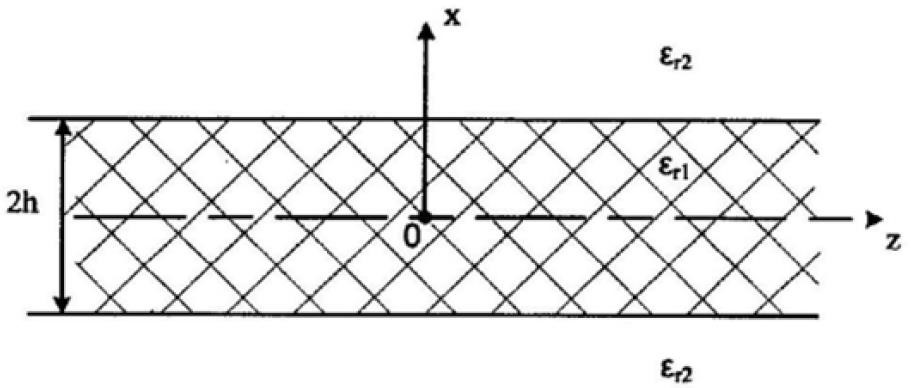
Задание 1:

Определить комплексные амплитуды всех проекций у векторов Em и Hm в средах 1 и 2 при x>=0.

.

.

Комплексные амплитуды всех проекций

.

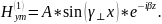
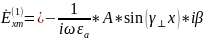Задание 2:

Составить и совместно решить уравнения, связывающие неизвестные поперечные волновые числа в средах 1 и 2, т.е. и .

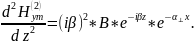
Сложив уравнения, получаем:

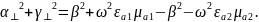
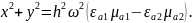
Граничные условия при x=h требуют равенства :

Граничные условия при x=h требуют равенства :

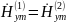Тогда, вычитая из , мы получим:

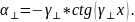
Домножив на h ,получаем:

.

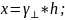
Задание 3:

Определить минимальную и максимальную толщины световода, при которых по нему будет распространяться только волна низшего типа.

Определим радиус R:

Из условия одноволнового режима (одна точка пересечения) 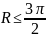, находим максимально возможную толщину h:

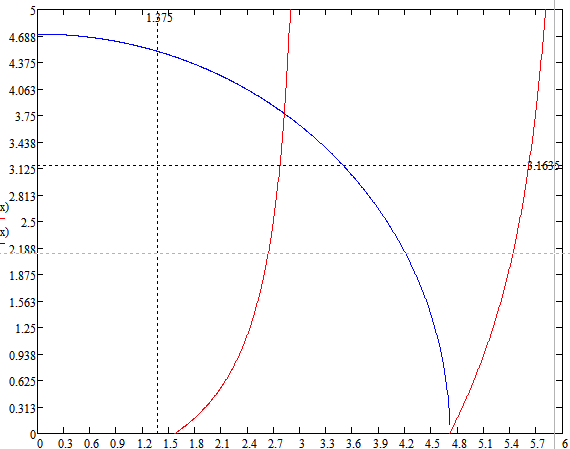
Рисунок 1 – Решение трансцендентного уравнения при максимальном h.

Из условия находим минимальную толщину h, начиная с которой существует одноволновый режим:

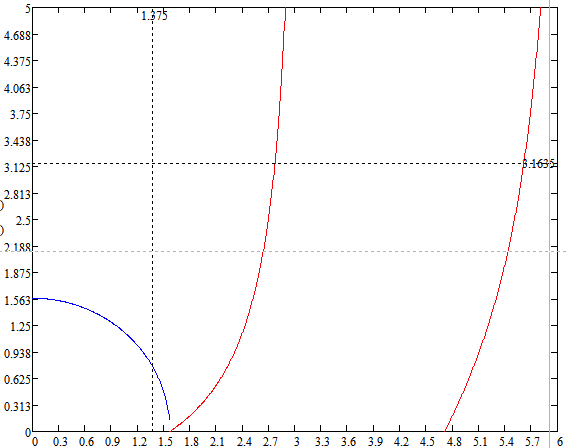
Рисунок 2 – Решение трансцендентного уравнения при минимальном h.

Найдем среднюю h волновода:

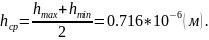
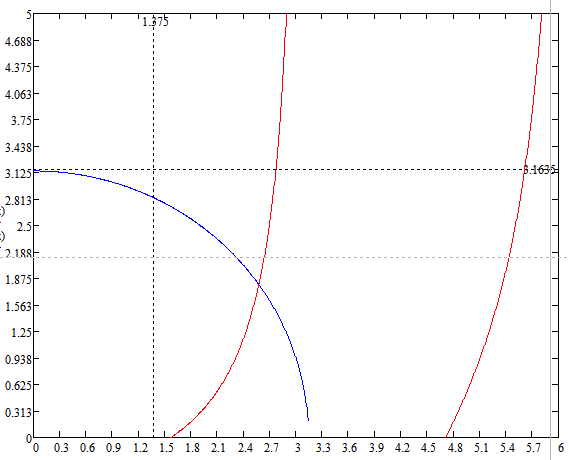
Рисунок 3 – Решение трансцендентного уравнения при среднем h.

Задание 4:

Для средней толщины световода вычислить параметры волны низшего типа и .

Для толщины волновода h трансцендентные уравнения принимают вид:

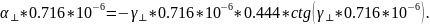
Получаем:

Определим постоянные распространения волны в световоде:

Фазовая скорость волны в световоде находится по формуле:

Задание 5:

Определить амплитуды A и B, входящие в выражения для всех проекций векторов.

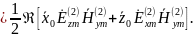
Подставляем значения и получаем:

Поскольку знак минуса указывает только на направление потока, то можно взять значение по модулю:

Тогда выразим из получившегося выражения амплитуду B:

Коэффициент A можно найти из граничных условий:

Задание 6:

Построить зависимости амплитуд всех проекций векторов и от координаты в области и в области .

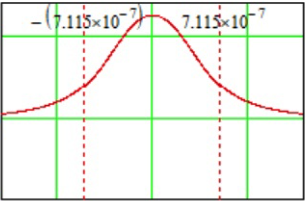
Рисунок 4 – Зависимость амплитуд Exm от X.

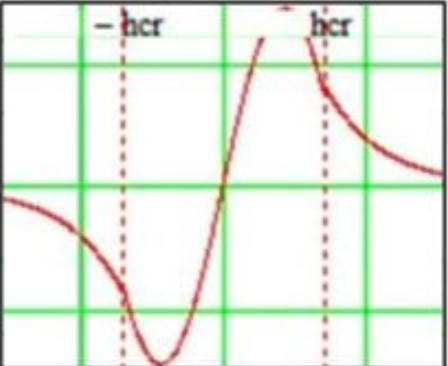
Рисунок 5 – Зависимость амплитуды Ezm от X.

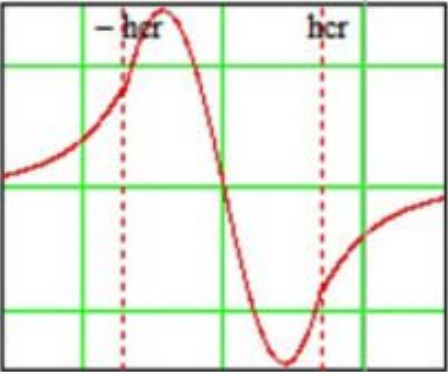
Рисунок 6 – Зависимость амплитуды Hym от X.