
Домашка ВАР5
.docxМИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное
учреждение высшего образования
“Московский технический университет связи и информатики”
( МТУСИ)
МТУСИ)
Кафедра "Техническая электродинамика и антенны"
Домашнее задание
по курсу Электродинамика и распространение радиоволн
"Электромагнитное поле в световоде"
Вариант 5.
Выполнил:
Студент группы
Проверила:
Москва 2024г.
Задание
Задача № 2-2
На
рисунке 1 показано продольное сечение
плоского световода ( ),
помещенного в неограниченную среду с
диэлектрической проницаемостью
),
помещенного в неограниченную среду с
диэлектрической проницаемостью
 .
Известны выражения для составляющих
векторов поля:
.
Известны выражения для составляющих
векторов поля:
В среде 1:
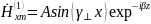 ,
,
 .
.
В среде 2:
 ,
,
 ,
,
где
А и В – постоянные, имеющие размерность
амплитуды поля,
 и
и
 - поперечные волновые числа в средах 1
и 2,
- поперечные волновые числа в средах 1
и 2,
 -
коэффициент фазы волны. Исходные данные:
-
коэффициент фазы волны. Исходные данные: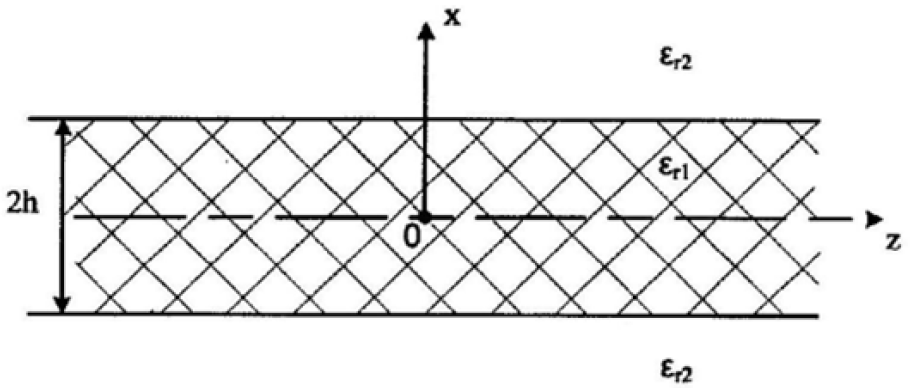
|
|
|||||
№ варианта |
|
|
λ = 2h, мкм |
f, ТГц |
|
|
05 |
2.25 |
1 |
1.6 |
187.5 |
– |
1.0 |
Даны
комплексные амплитуды x-составляющих
векторов

Определим
комплексные амплитуды всех проекций
 в
средах 1 и 2.
в
средах 1 и 2.
Уравнение связи:









Для
первой среды найдем
 :
:

Так
как



Найдем производные. Производная комплексной амплитуды z-составляющей по координате x и x-составляющей по координате z в первой среде:


Найдем производные. Производная комплексной амплитуды x-составляющей по координате z и z-составляющей по координате x во второй среде:


Найдём
 и
и
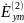 :
:


Найдём
 ,
, ,
,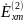 и
:
и
:

В
итоге имеем для комплексных амплитуд
составляющих векторов
 .
Для 1 среды:
.
Для 1 среды:
Для 2 среды:
Рассмотрим
применение граничных условий на границе
раздела (при
 ):
):

Из данных равенств, зная выражения для комплексных амплитуд составляющих векторов для 1 и 2 сред, можно записать:

Упрощаем полученное равенство:

Также
для вектора
 можно записать и упростить равенство:
можно записать и упростить равенство:

Система уравнений теперь имеет вид:

Делим первую составляющую системы на вторую и получаем:

Теперь
запишем уравнение Гельмгольца для
получения равенства между суммой
квадратов поперечных волновых чисел
 (для
2 среды) и разностью квадратов коэффициентов
(для
2 среды) и разностью квадратов коэффициентов

Уравнения Гельмгольца для 1 и 2 сред:


где
 - оператор Гамильтона.
- оператор Гамильтона.

Найдем
 :
:

Заменим
выражение
 на
на
 и запишем итоговое выражение для
уравнения Гельмгольца для 1 среды:
и запишем итоговое выражение для
уравнения Гельмгольца для 1 среды:

Данное выражение можно привести к упрощенному виду:

Теперь, по аналогии, запишем выражение для уравнения Гельмгольца для 2 среды:



Итого:
Приравниваем данные выражения и получаем:
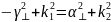
Переписываем в более удобной форме:

Запишем систему уравнений:

 ,
,
 .
.
Где
 - абсолютная диэлектрическая проницаемость
1 среды, Ф/м;
- абсолютная диэлектрическая проницаемость
1 среды, Ф/м;
 -
абсолютная диэлектрическая проницаемость
2 среды, Ф/м;
-
абсолютная диэлектрическая проницаемость
2 среды, Ф/м;
 – электрическая
постоянная, Ф/м;
– электрическая
постоянная, Ф/м;
 – магнитная
постоянная, Гн/м;
– магнитная
постоянная, Гн/м;
 – циклическая
частота электромагнитных колебаний,
рад/с.
– циклическая
частота электромагнитных колебаний,
рад/с.
В первом уравнении системы выразим поперечное число для второй среды:

Домножим каждый член системы уравнений на h:


Произведем
замену переменных:
 и
и


Второе
уравнение системы представляет собой
уравнение окружности с радиусом R= .
Запишем итоговую систему уравнений:
.
Запишем итоговую систему уравнений:

Р
Найдем R2:


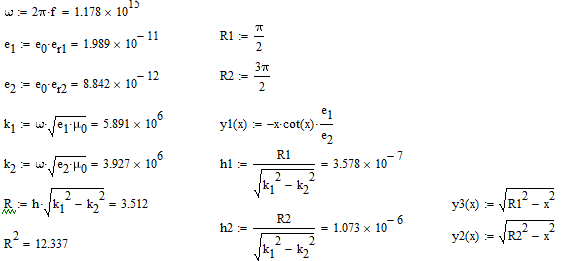
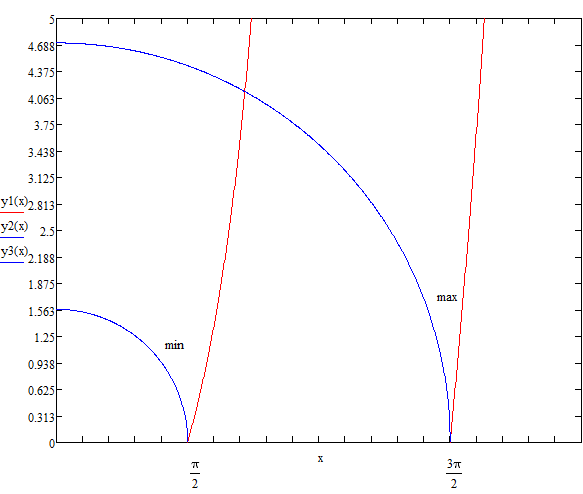
Рисунок 2 – Графическое решение системы уравнений
Решение системы уравнений есть среднее арифметическое между минимум и максимумом:
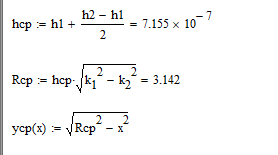
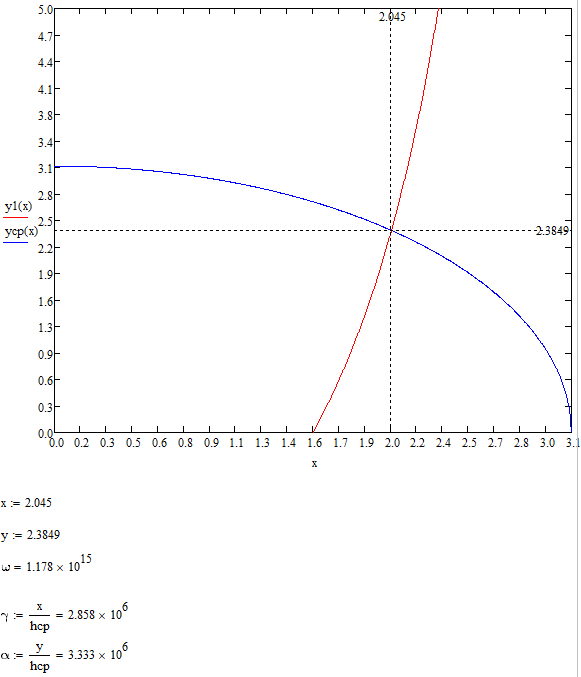
Параметры
 были определены:
были определены:


Найдем
, выражая его из следующих формул:
 и
и
 :
:


Рассчитаем по двум вышеуказанным формулам:
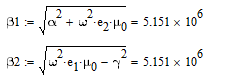
В обоих случаях результаты одинаковы, следственно, расчет был произведен верно.
Значение фазовой скорости найдем из следующего выражения:

![]()
Используя
заданную величину единичной мощности
волны в среде 2, т.е.
 ,
определим амплитуды A
и B,
входящие в выражения для всех проекций
векторов
,
определим амплитуды A
и B,
входящие в выражения для всех проекций
векторов
 и
.
и
.
Запишем выражение для вектора Пойнтинга во второй среде. Комплексный вектор Пойнтинга определяется как половина векторного произведения комплексной амплитуды вектора напряжённости электрического поля на комплексно-сопряжённое комплексной амплитуды вектора напряжённости магнитного поля. Составляющие полей нам известны, подставляем их в формулу, упрощаем выражение.

Для решения данной задачи понадобится только z-ая компонента вектора Пойнтига, перепишем:

Комплексно-сопряжённое комплексной амплитуды вектора напряжённости магнитного поля:



Запишем
выражение для




Выразим отсюда В:
 =
=
Рассчитаем В:
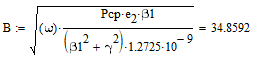
Расчет A произведем из уравнения граничных условий пункта 2:


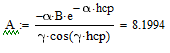
Произведем расчет и построение зависимости y-составляющей вектора от координаты х в 1 и во 2 средах:

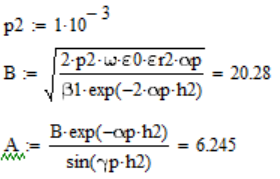


Рисунок 3 – Зависимость x-составляющей вектора от координаты x в 1 и во 2 средах
Произведем расчет и построение зависимости z-составляющей вектора от координаты х в 1 и во 2 средах:


Рисунок 4 – Зависимость z-составляющей вектора от координаты x в 1 и во 2 средах
За
Произведем расчет и построение зависимости y-составляющей вектора от координаты х в 1 и во 2 средах:
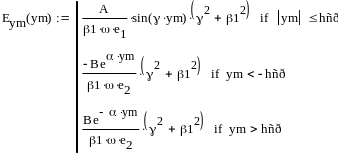

Рисунок 5 – Зависимость y-составляющей вектора от координаты х в 1 и во 2 средах




 мВт
мВт мВт
мВт


