ЛАБ24 сверточные коды

Министерство цифрового развития, связи и массовых коммуникаций

Российской Федерации

Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СВЯЗИ И ИНФОРМАТИКИ

(МТУСИ)

Факультет "Радио и телевидение"

Кафедра "Радиотехнические системы"

Лабораторная работа №24-а

По дисциплине "Помехоустойчивое кодирование":

"Построение и исследование кодека со свёрточным кодом"

Выполнил:

Студенты группы

Проверила:

Москва 2025

Цель работы: изучение особенностей и характеристик свёрточных кодов, а также принципов работы кодирующих и декодирующих устройств и методов кодирования и декодирования.

Исходные данные:

– скорость кода;

– число инф. символов;

– инф. последовательность;

– образующий полином;

Расчетная часть:

По образующему полиному построим схему кодера:

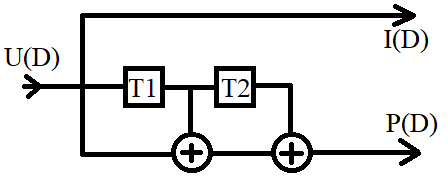
Рисунок 1 – Схема сверточного кодера

Для получения кодового слова на выходе сверточного кодера, необходимо построить решетчатую диаграмму или образующую матрицу.

Таблица 1 – Диаграмма состояний кодера

Вх. последовательность	Т1	Т2	Вых. последовательность
0	0	0	0		0
1	0	0	1		1
1	1	0	0		1
0	1	1	0		0
1	0	1	0		1
1	1	0	0		1
0	1	1	0		0
0	0	1	1		0

Таким образом выходные последовательности образуют кодовое слово:

Теперь составим порождающую матрицу, путем сдвига ИХ:

По полученной матрице тоже можно найти проверочное слово, для этого необходимо умножить матрицу на информационную последовательность:

Результаты сошлись.

Построим проверочную матрицу:

H(D) = , тогда: H^T(D)=

По проверочной матрице построим систему ортогональных проверок (S=3):

Если J=3, тогда П=2;

Лабораторная часть:

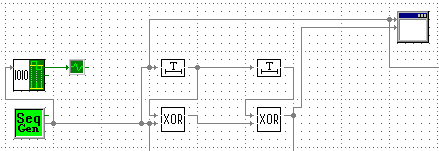
Рисунок 2 – Схема сверточного кодера в спектре

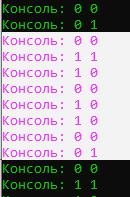
Рисунок 3 – Результат кодирования

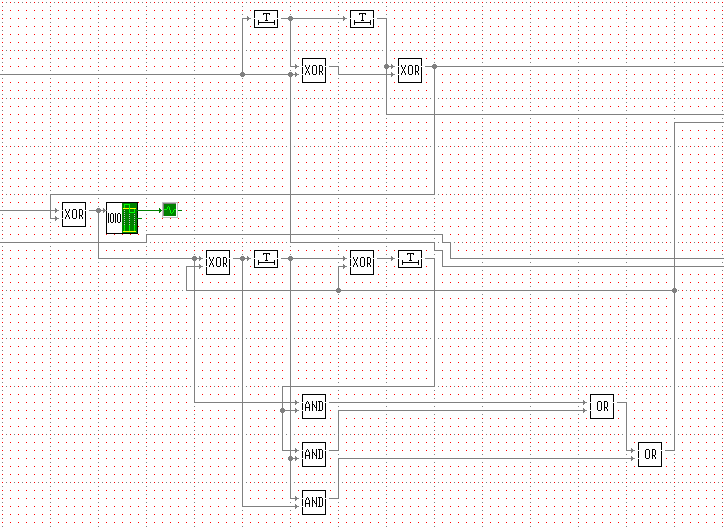
Рисунок 4 – Схема порогового декодера

Затухание в дБ	Без кодирования	С кодированием
1	0,005	0,001
5	0,056	0,039
10	0,188	0,183
15	0,37	0,31
20	0,419	0,383
25	0,456	0,433

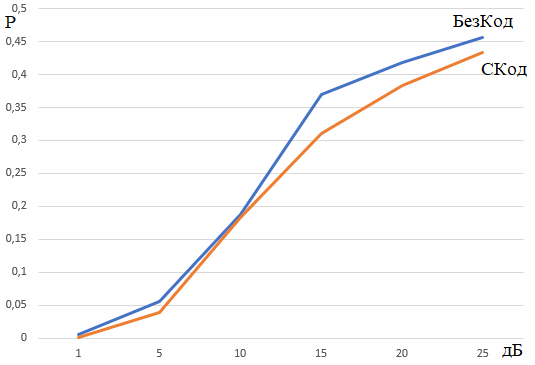
Рисунок 5 – Вероятность ошибки с/без коррекции от уровня шума в дБ

Вывод: в ходе лабораторной работы были построены схемы порогового кодера и декодера свёрточного кода, проведено сравнение экспериментальных результатов работы схем с теоретически рассчитанными результатами. Получена характеристика помехоустойчивости данного кода, которая показывает, что при уменьшении уровня шума в канале связи наблюдается уменьшение вероятности ошибочного декодирования.