
ЛАБ5 схемы дискретной логики
.docxМинистерство цифрового развития, связи и массовых коммуникаций
Российской Федерации
Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования
МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СВЯЗИ И ИНФОРМАТИКИ
(МТУСИ)
Факультет "Радио и телевидение"
Кафедра "Радиотехнические системы"
Лабораторная работа №5
По дисциплине "Помехоустойчивое кодирование":
"Построение и исследование схем дискретной логики, используемых при создании помехоустойчивых кодеков"
Выполнил:
Студенты группы
Проверила:
Старший преподаватель
Цель работы: изучение принципа построения и работы схем дискретной логики, используемых при создании помехоустойчивых кодеков.
Домашний расчет
Исходные данные по варианту 20:
Полином

Закодируем две буквы фамилии Шишков согласно таблице №1 методических указаний:

Умножим исходный полином на образующий:

1100001000
x 1011101
-----------------------------
1100001000
0000000000
1100001000
1100001000
1100001000
0000000000
1100001000
-----------------------------
1110010111101000 = C
Произведем деление
 :
:
1110010111101000 | 1011101
1011101 | 1100001
1011111
1011101
1011101
1011101
0
Произведем деление
 :
:
1110010111101010 | 1011101
1011101 | 1100001
1011111
1011101
1011101
1011101
0010
Остаток – 10.
Лабораторная часть
1) Построение регистра сдвига битовых последовательностей.

Рисунок 1 – Регистр сдвига битовых последовательностей
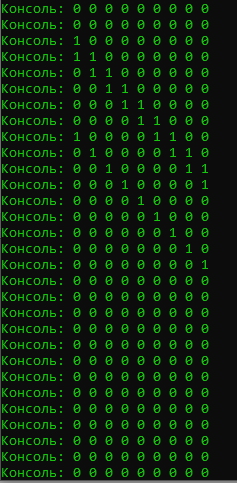
Рисунок 2 – Данные битовой консоли для регистра сдвига
Сохранённые бинарные данные представлены ниже, в них тоже видна периодически повторяющаяся входная последовательность за исключением того, что она выходит младшими битами вперёд, а в начале последовательности есть нулевые биты, соответствующие выходу заранее заданных нулевых состояний регистров сдвига.
2А) Построение схемы перемножения полиномов-битовых последовательностей по схеме Фибоначчи.
Отводы от регистров на элементы сложения по модулю 2 соответствуют умножению входной последовательности на полином:


Рисунок 3 – Перемножитель полиномов-битовых последовательностей по схеме Фибоначчи.

Рисунок 4 – Данные битовой консоли при работе схемы Фибоначчи для умножения полиномов
Выходная
последовательность, соответствует
предварительно рассчитанному произведению
 .
.
2Б) Построение схемы перемножения полиномов-битовых последовательностей по схеме Галуа.
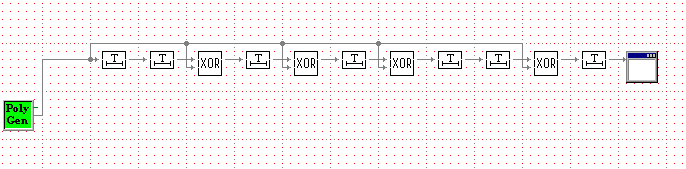
Рисунок 5 – Перемножитель полиномов-битовых последовательностей по схеме Галуа.

Рисунок 6 – Данные битовой консоли при работе схемы Фибоначчи для умножения полиномов
Выходная последовательность, соответствует предварительно рассчитанному произведению .
3А) Построение схемы деления полиномов-битовых последовательностей по схеме Фибоначчи.

Рисунок 7 – Делитель полиномов-битовых последовательностей по схеме Фибоначчи

Рисунок 8 – Данные битовой консоли при работе схемы Фибоначчи для делителя полиномов
3Б) Построение схемы деления полиномов-битовых последовательностей по схеме Галуа.
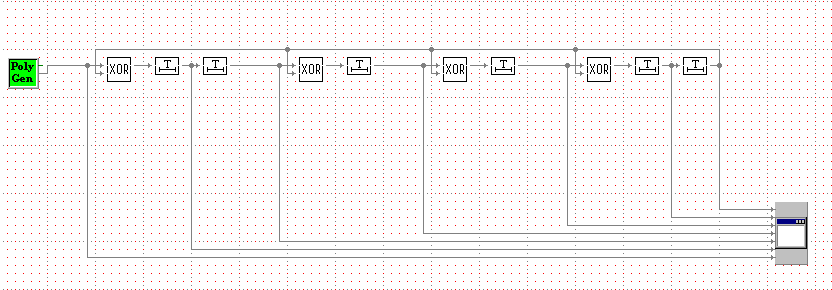
Рисунок 9 – Делитель полиномов-битовых последовательностей по схеме Галуа
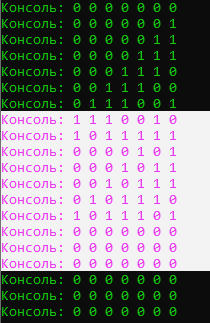
Рисунок 10 – Данные битовой консоли при работе схемы Галуа для делителя полиномов
4А) Построение схемы генератора псевдослучайной последовательности по схеме Фибоначчи.
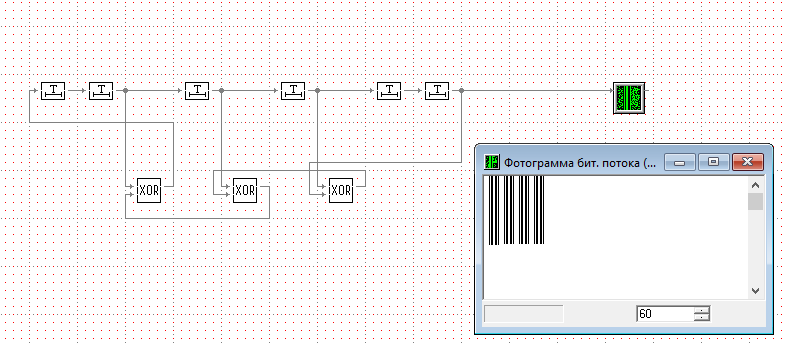
Рисунок 11 – Схема генератора псевдослучайной последовательности по схеме Фибоначчи и результат работы фотограммы
Период генерируемой ПСП равен 60.
4Б) Построение схемы генератора псевдослучайной последовательности по схеме Галуа.
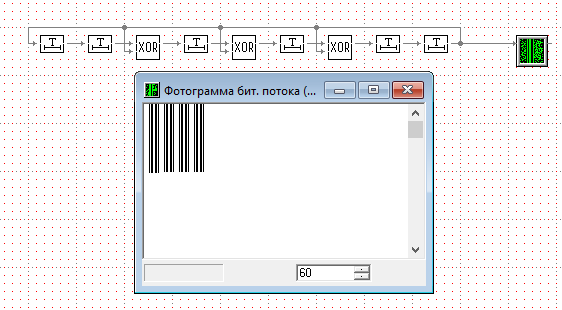
Рисунок 12 – Схема генератора псевдослучайной последовательности по схеме Галуа и результат работы фотограммы
Период генерируемой ПСП равен 60.
Вывод:
1) Изучен принцип работы умножителя многочленов на элементах дискретной логики по схемам Галуа и Фибоначчи. Результаты, полученные в лабораторной части, совпали с данными домашнего расчёта.
2) Изучен принцип работы делителя многочленов на элементах дискретной логики по схемам Галуа и Фибоначчи. Результаты, полученные в лабораторной части, совпали с данными домашнего расчёта
3) На базе схем деления полиномов построены схемы генераторов псевдослучайных последовательностей. Период ПСП, генерируемой по лабораторному заданию равен (не равен) максимально возможному значению 2n-1, где n –порядок образующего многочлена g(x). Причина этого в том, что g(x) …приводимый (неприводимый многочлен.
Москва 2024
