ЛАБ2 циклические коды
.docxМинистерство цифрового развития, связи и массовых коммуникаций
Российской Федерации
Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования
МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СВЯЗИ И ИНФОРМАТИКИ
(МТУСИ)
Факультет "Радио и телевидение"
Кафедра "Радиотехнические системы"
Лабораторная работа №2
По дисциплине "Помехоустойчивое кодирование":
"Исследование процессов кодирования и декодирования циклических кодов"
Выполнил:
Студенты группы
Проверила:
Москва 2024
Цель работы:
1. Получение практических навыков по формированию порождающего многочлена для построения циклических кодов, изучение способов построения порождающей и проверочной матриц, способов формирования кодовых слов и схемной реализации кодирующих устройств.
2. Изучение процессов декодирования циклических кодов, принципа построения и работы декодеров с обнаружением и исправлением ошибок в кодовых словах.
3. Исследование помехоустойчивости циклических кодов.
Исходные данные:
Вариант |
n |
k |
g(x) |
Входное воздействие a(x) |
20 |
9 |
4 |
|
111100000 |
Расчетная часть:
Для построения проверочной матрицы нужно вычислить ее ряд:
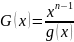
1000000001 | 111011
111011 | 11010
110110
111011
110100
111011
111101
111011
110
Составим порождающую систематическую матрицу: G(x) =
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
Составим проверочную матрицу: H(x) =
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
Составим таблицу синдромов:
S |
Ошибка в символе |
Конфигурация ошибки |
S0 = 01111 |
A1 |
100000000 |
S1 = 11010 |
A2 |
010000000 |
S2 = 01101 |
A3 |
001000000 |
S3 = 11011 |
A4 |
000100000 |
Для
исправления независимых ошибок кратности
t
= 1, требуется кодовое расстояние
 .
Коды (9,4) имеют кодовое расстояние от 3
до 5.
.
Коды (9,4) имеют кодовое расстояние от 3
до 5.
Найдем число М из соотношения:
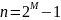
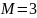
Тогда число проверочных символов:
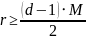
Входная последовательность: 111100000
Так
как код (9.4), то информационная
последовательность будет: 1111 или
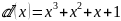 .
.
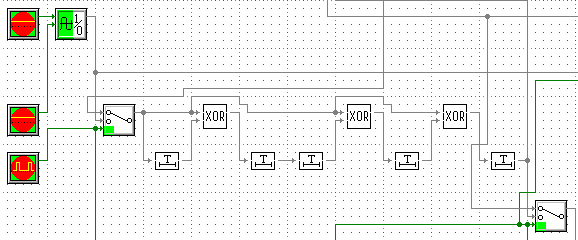
Рисунок 1 – Схема кодера
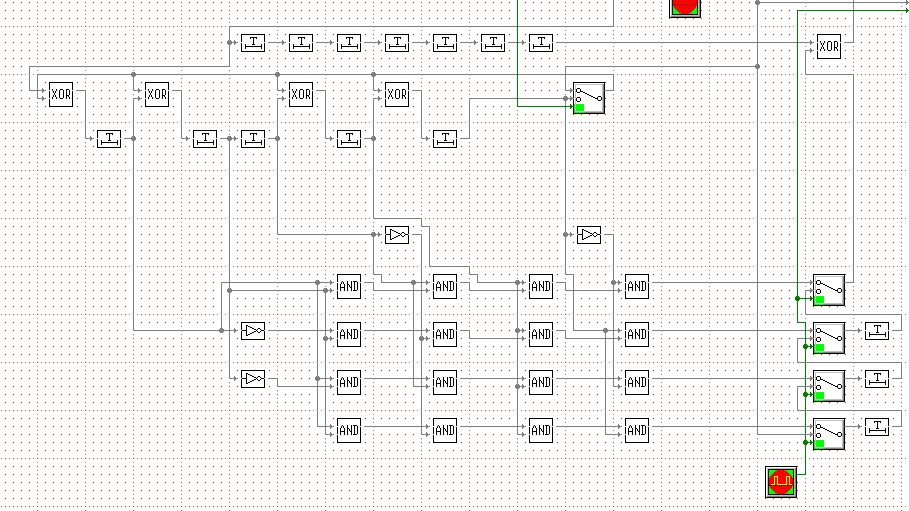
Рисунок 2 – Схема декодера
Рисунок 3 – Результат работы схемы
Затухание (дБ) |
Вероятность ошибки без учета коррекции |
Вероятность ошибки с учетом коррекции |
1 |
0,051 |
0,034 |
2 |
0,067 |
0,043 |
5 |
0,151 |
0,141 |
10 |
0,269 |
0,273 |
15 |
0,362 |
0,36 |
20 |
0,4 |
0,4 |
25 |
0,44 |
0,44 |

Рисунок 4 – Зависимость вероятности ошибки от уровня затухания