Laba_5_metrologia

Минобрнауки России

Федеральное государственное бюджетное образовательное

учреждение высшего образования

«Юго-Западный государственный университет»

Лабораторная работа № 5

по дисциплине «Метрология»

«Исследование параметров сигналов с помощью электронно-лучевого осциллографа»

Выполнил: ст.гр. ИБ-21б

Карапетян Т.М.

Рохтин Я.А

Проверил: ст. преп. Коломиец Е.А.

Курск 2024 г.

Цель работы

Овладение методикой измерения фазовых, частотных и временных параметров периодических сигналов с помощью осциллографа. Получение навыков работы с измерительными генераторами.

Ход работы

На рисунке 1 представлены все приборы, используемые в работе.

Рисунок 1 – Приборы, используемые в работе

Измерим разность фаз, сдвинутых по фазе двух синусоидальных колебаний, с помощью двухканального осциллографа и оценим погрешность измерений (рис. 2).

В общем случае разность фаз определяется выражением

φ = ∙ 360°

В нашем случае = 1,4 а Т = 7,5 тогда получим

φ = ∙ 360° = 67,2 °

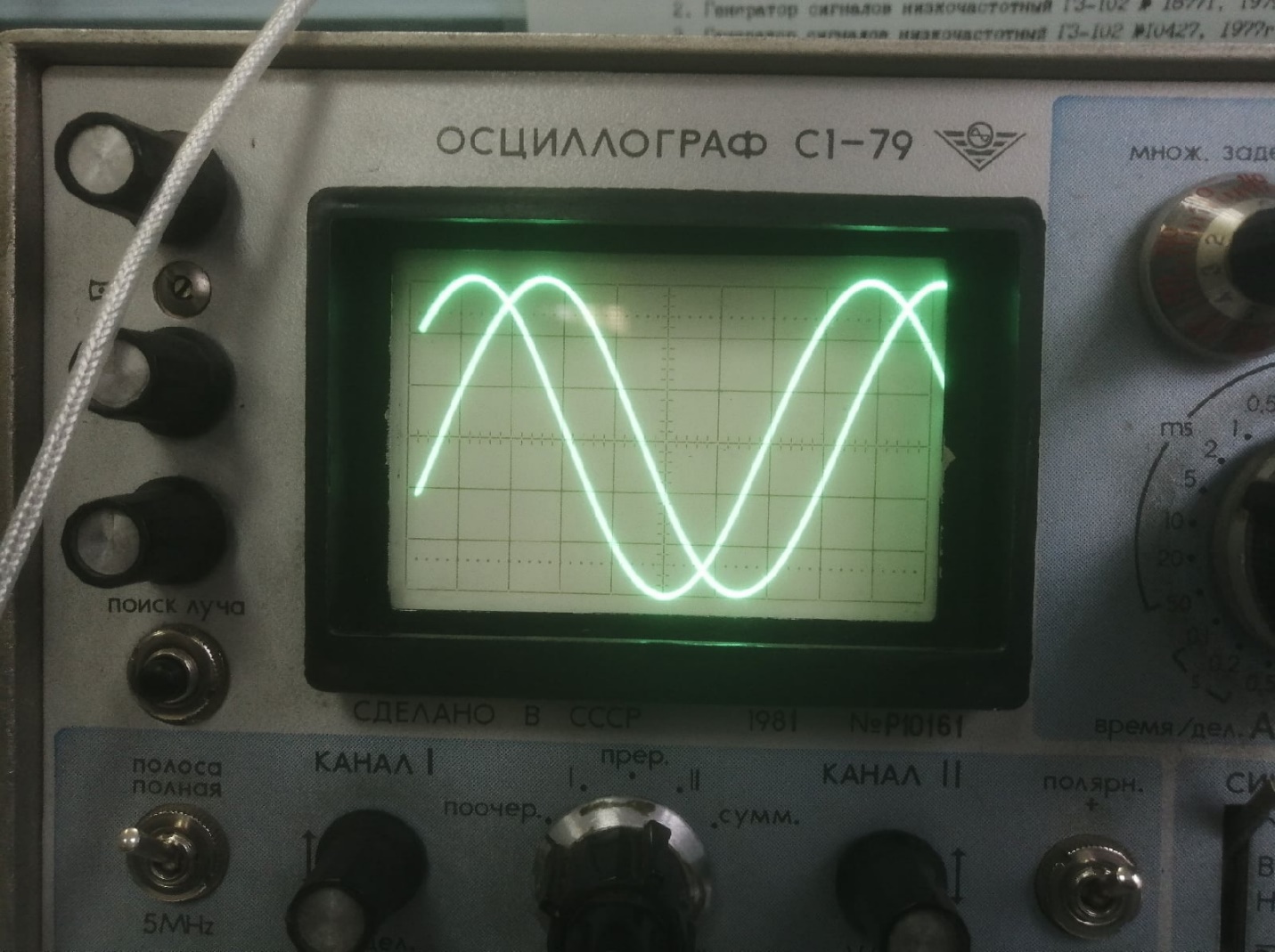
Рисунок 2 – Измерение разность фаз двухканального осциллографа

 Так как при измерении разности фаз использовался косвенный метод, то погрешность измерения ∆φ может быть определена как

Из этого можем получить, что погрешность измерения ∆φ равна:

= 0,015 = 1,5%

Измерим те же разности фаз однолучевым и двухканальным осциллографом в режиме эллиптической развертки и оценим погрешности измерений (рис. 2).

Рисунок 2 – Измерение разности фаз двух синусоидальных сигналов методом эллипса

Для измерения разности фаз двух синусоидальных сигналов методом эллипса нам понадобятся следующие формулы:

sin φ = ; sin φ = =

Исходя из рисунка эллипса имеем такие значения: В = 3,8; Xm = 4,3; A=2,1; Ym = 2,4. Подставив их в формулы получим следующие значения:

sin φ = = 0,88 ± 2%;

sin φ = = 0,88 ± 2%;

φ=61^о

Измерим частоту синусоидального сигнала методом непосредственной оценки с помощью калиброванной развертки (рис. 3). При этом измерим период колебания Т и определим частоту f как величину обратную периоду: f=1/T.

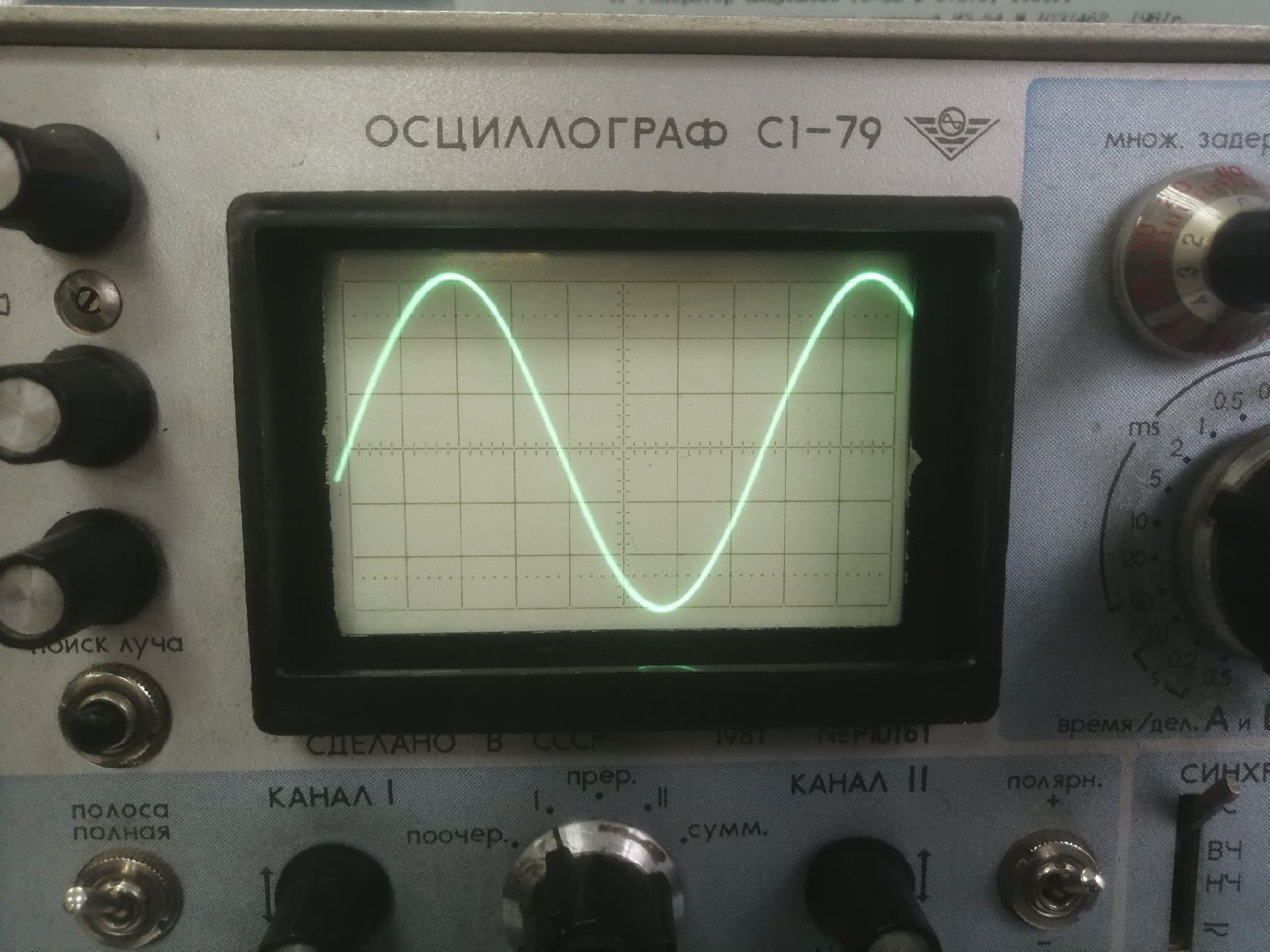
Рисунок 3 – Измерение частоты синусоидального сигнала методом непосредственной оценки

В таком случае период колебания будет равен Т = 8,5 ∙ 50 мкс = 425 мкс.

Определим частоту, она будет равна:

f = = 2352,94 Гц ± 4,5%

Более точные результаты измерения частоты синусоидального сигнала может дать метод сравнения, при котором осциллограф используется как индикатор равенства или кратности частот. 

Измерим частоту того же синусоидального сигнала методом сравнения при помощи двухканального осциллографа (рис. 4).

При непосредственном сравнении сигналов с помощью двухлучевого осциллографа производится прямое сопоставление сигналов (измеряемого и опорного), отображаемых по двум каналам осциллографа. При этом исследуемый сигнал подается на вход канала 1, а опорный на вход канала 2.

F_Э = 25,1 * 10² = 2510 Гц

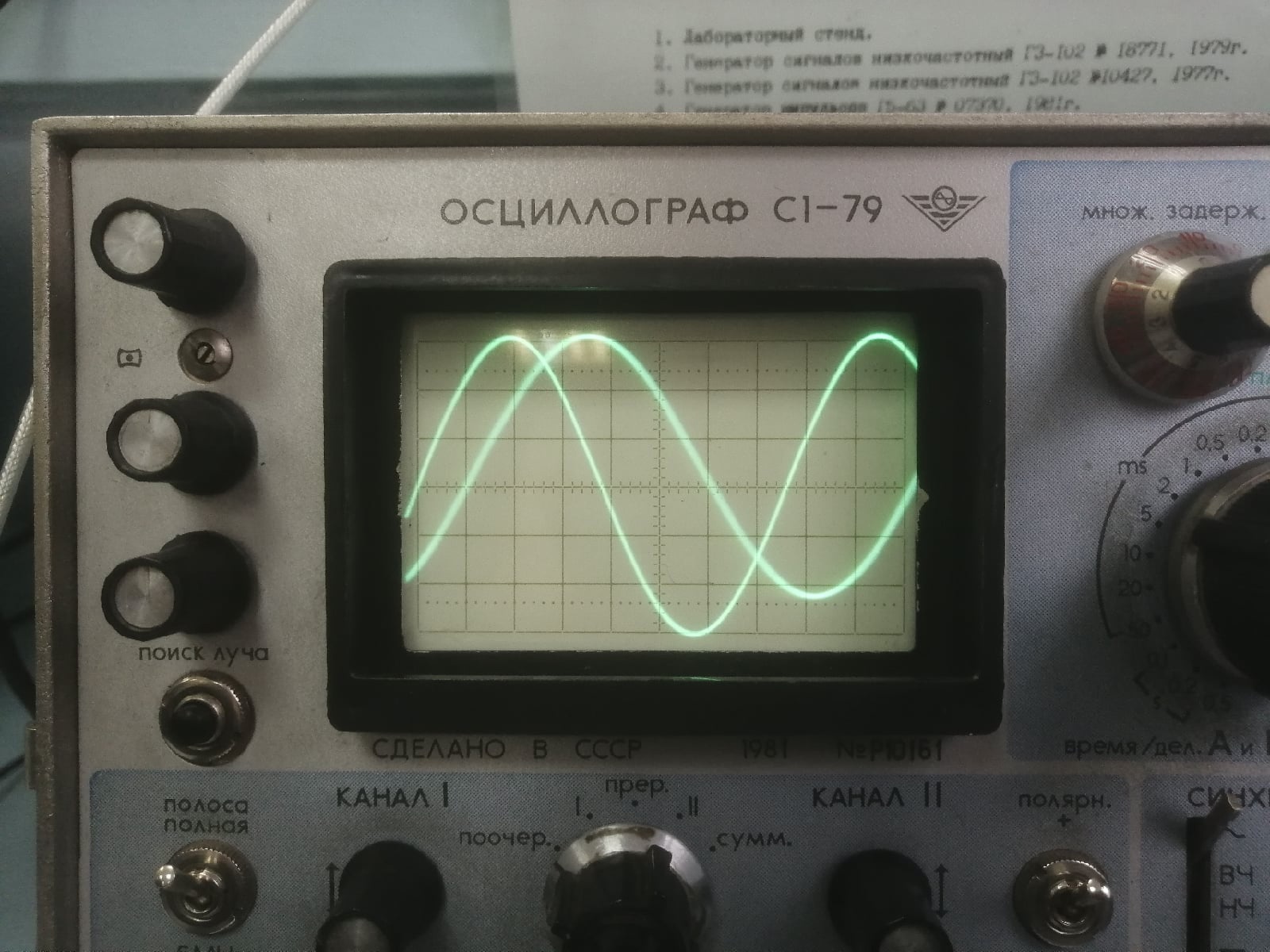
Рисунок 4 – Измерение частоты синусоидального сигнала методом сравнения

Измерим частоту того же синусоидального сигнала методом фигур Лиссажу.

Для реализации метода фигур Лиссажу измеряемый сигнал подается на вход У, а опорный - на вход X осциллографа, при этом осциллограф должен быть переведен в режим синусоидальной (эллиптической) развертки (внутренняя развертка должна быть отключена). В общем случае для определения кратности достаточно мысленно провести горизонтальную и вертикальную линии и взять отношение количества точек пересечения с фигурой в горизонтальной и вертикальной плоскости:

Проведём три измерения частот при различных кратностях и оценим ошибку измерения.

В первом измерении частота при кратности f1 будет равна (рисунок 5):

fопор. = f1; К = 2/2 = 1

Рисунок 5 – Измерение первой частоты

В втором измерении частота при кратности f2 будет равна (рисунок 6):

fопор. = f2; К = 4/2 = 2

Рисунок 6 – Измерение второй частоты

В третьем измерении частота при кратности f3 будет равна (рисунок 7):

fопор. = f3; К = 6/2 = 3

Рисунок 7 – Измерение третьей частоты

Измерим частоту того же синусоидального сигнала методом темновых меток.

Для измерения частоты методом темновых меток осциллограф переводится в режим круговой развертки. При этом на вход У подается исследуемый сигнал, а на вход X - тот же сигнал, но сдвинутый по фазе. В результате на экране осциллографа будет отображаться эллипс.

Проведём три измерения частот при различных кратностях и оценим ошибку измерений.

В первом измерении при fопор. = f1 имеем 1 темневую метку (рисунок 8).

Рисунок 8 – Измерение первой частоты с 1 меткой

Во втором измерении при fопор. = f2 имеем 2 темневые метки (рисунок 9).

Рисунок 9 – Измерение второй частоты с 2 метками

В третьем измерении при fопор. = f3 имеем 3 темневые метки (рисунок 10).

Рисунок 10 – Измерение третьей частоты с 3 метками

Вывод

В ходе лабораторной работы мы ознакомились с методикой измерения фазовых, частотных и временных параметров периодических сигналов с помощью осциллографа, и получили навыки работы с измерительными генераторами.