
lab_4_TS_Ivanova_4117
.docxГУАП
КАФЕДРА № 41
ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ
ПРЕПОДАВАТЕЛЬ
ассистент |
|
|
|
Б. К. Акопян |
должность, уч. степень, звание |
|
подпись, дата |
|
инициалы, фамилия |
ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №4 |
ОЦЕНКА СТРУКТУРНОЙ СЛОЖНОСТИ ИНФОРМАЦИОННЫХ ПРОБЛЕМ |
по курсу: ТЕОРИЯ СИСТЕМ И СИСТЕМНЫЙ АНАЛИЗ |
|
|
РАБОТУ ВЫПОЛНИЛ
СТУДЕНТ ГР. № |
4117 |
|
|
|
А.В.Иванова |
|
|
|
подпись, дата |
|
инициалы, фамилия |
Санкт-Петербург 2023
Цель работы:
Научиться анализировать архитектуру существующей информационной системы и представлять ее в виде модели структуры.
Выполнение работы:
Для оценивания структурной сложности системы исследуется ориентированный взвешенный граф, соответствующий этой системе. Структурная сложность оценивается по нескольким критериям, а именно по количеству дуг, бикомпонент и контуров в графе.
Рассматриваемая система Android Studio – содержит большое число элементов, поэтому для удобного представления структуры системы они были обозначены буквами латинского алфавита, как приведено в таблице № 1.
Таблица № 1 – Обозначение элементов системы
Название |
Обозначение |
Среда передачи динамичных данных |
a |
Подсистема навигации по коду |
b |
Подсистема хранения данных |
c |
Подсистема сборки программы |
d |
Подсистема вычислений |
e |
Подсистема пользовательского интерфейса |
f |
Подсистема исполнения команд |
g |
Среда передачи статичных данных |
h |
Ядро |
i |
Android SDK |
j |
JDK |
k |
Кэш |
l |
Библиотеки |
m |
Данные VCS |
n |
Файлы проектов |
o |
Исполняемые файлы |
p |
GPU |
q |
Журнал изменений |
r |
Основываясь на построенной в первой лабораторной схеме системы для введённых обозначений выведена матрица смежности, которая отображает наличие связей между элементами и их направление. Построенная матрица отображена в таблице № 2.
Таблица № 2 – Матрица смежности
|
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
a |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
b |
|
|
|
|
|
|
|
1 |
|
|
|
1 |
1 |
|
|
|
|
|
c |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
1 |
|
|
|
d |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
e |
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
g |
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
h |
|
1 |
1 |
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
i |
1 |
1 |
|
1 |
|
|
|
1 |
|
1 |
|
|
|
|
|
|
1 |
|
j |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
k |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
o |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Для упрощенного рассмотрения узлов и связей системы на рисунке № 1 приведен ориентированный граф, соответствующий матрице смежности.
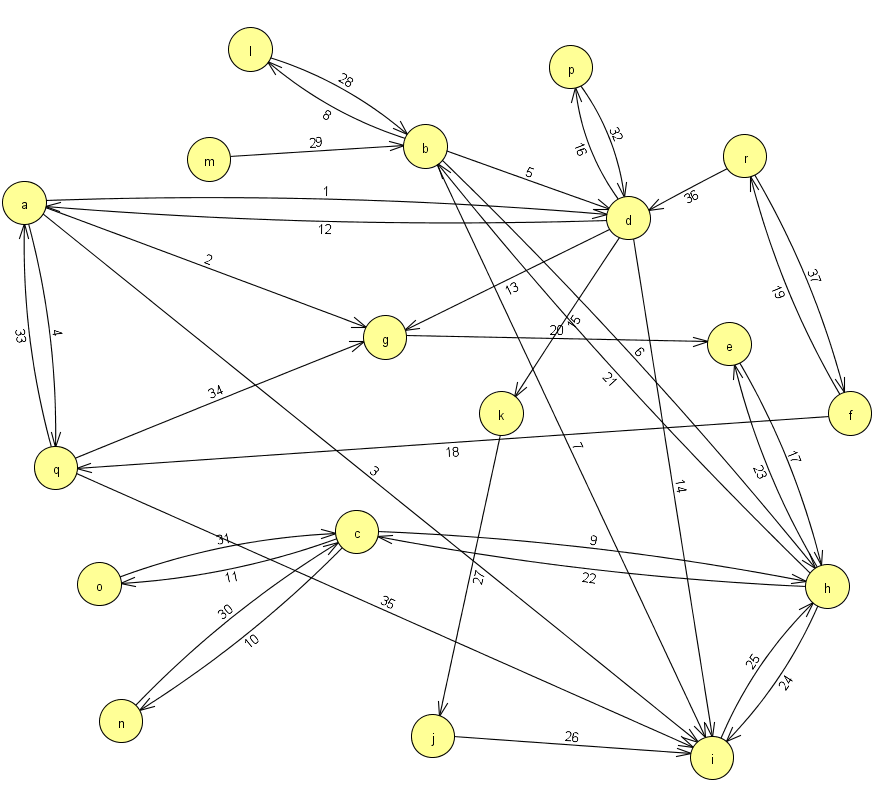
Рисунок № 1 – Граф, соответствующий матрице смежности
Определить число дуг в заданном графе позволяет матрица инцидентности. Вертикальную ось матрицы занимают обозначения элементов системы – узлы, а горизонтальную – связи между ними. Всего насчитывается 37 дуг. Для каждой связи указаны её конец (-1) и начало (1).
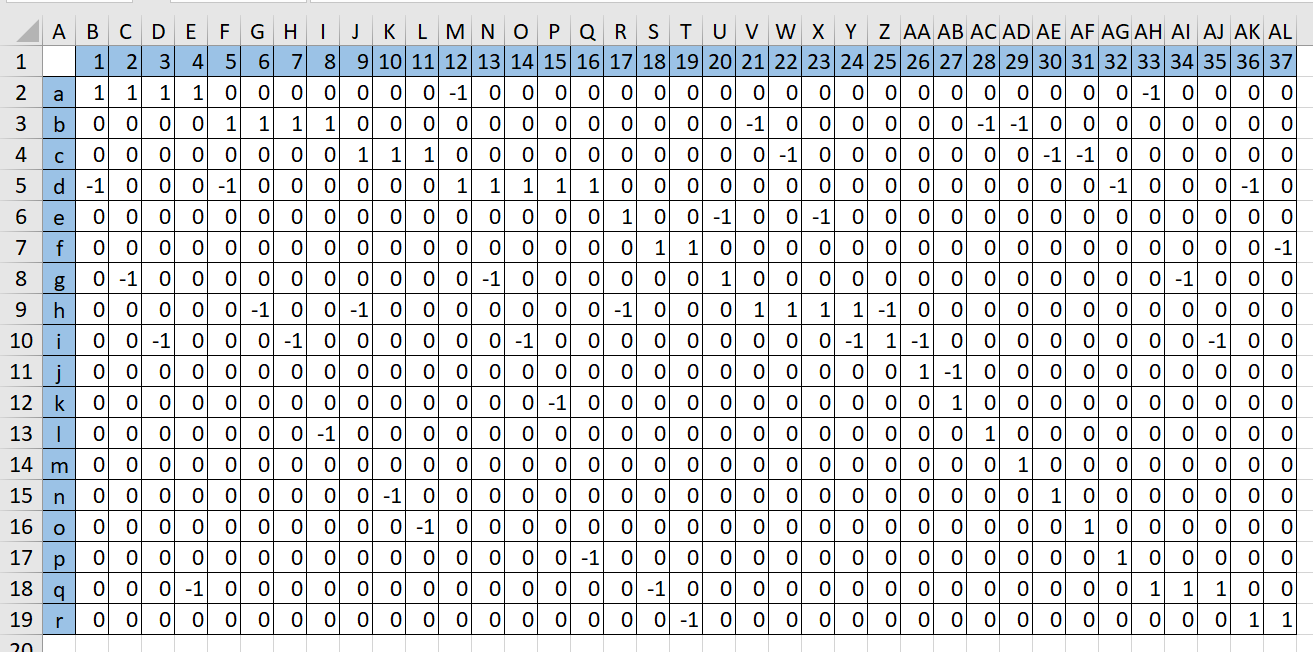
Рисунок № 2 – Матрица инцидентности
Бикомпонента является максимальным по включению сильно связанный подграфом графа. В больших графах, наподобие этого, сложно выделить бикомпоненты по виду графа. Поэтому была построена матрица достижимости, приведенная в таблице № 3. По данной матрице можно быстро определить, можно ли из одной вершины попасть в другую. Так как почти все рассматриваемые элементы системы тесно связаны между собой и почти все затрагивают работу с системами передачи динамических и статичных данных, получается, что практически из любого узла можно добраться в иной. А такие компоненты как Библиотеки, Журнал исполнения команд и Пользовательский интерфейс можно назвать несколько обособленными от остальных, так как они являются сторонними в процессе сборки программы. Например система навигации, а за ней и система сборки используют готовый код из библиотек, но обратной связи между ними нет. Также и пользовательский интерфейс с журналом команд используются для вывода на экран результатов сборки, но не участвуют в данном процессе.
Таблица № 3 – Матрица достижимости
|
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
a |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
b |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
c |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
d |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
e |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
f |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
g |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
h |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
i |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
j |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
k |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
l |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
m |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
n |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
o |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
p |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
q |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
r |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
