
Дополнительное задание:
Составить другую модель для 1 задачи, добавив в неё слоев, нейроном и применив слои Dropout.
Основная проблема первой модели состоит в её больших значениях ошибки и стремительном переобучении при попытке увеличить количество нейроном в каком-либо из слоев.
Модель усложнена, теперь она состоит из 4 слоев, количество нейронов во входном и скрытых слоях увеличено: 64, 64 и 16 соответственно. На выходном нейроне добавлена функция активации Relu, чтобы разграничить получаемые оценки. Код дополнительного задания содержится в Приложении C.
Во избежание переобучения между слоями добавлены слои Drouput(0.2), которые обнуляют 20% случайных выходов нейронов после их вычисления. Обучение представлено на Рисунке 15.

Рисунок 15 – Обучение новой модели
Однако обучение видоизменённой модели не дало улучшения результатов, кроме того, что была достигнута меньшая разница между потерями на тренировочных и валидационных данных.
Данная модель также сталкивается с проблемой переобучения при изменении числа эпох / нейронов в слоях. Можно сделать вывод, что данный датасет не содержит выраженных признаков, позволяющих эффективно решать задачу регрессии.
На графике изменения потерь (Рисунок 16) для тренировочных и валидационных данных видно схожесть с результатами первой модели, но и разницу в меньшем разбросе между функциями.
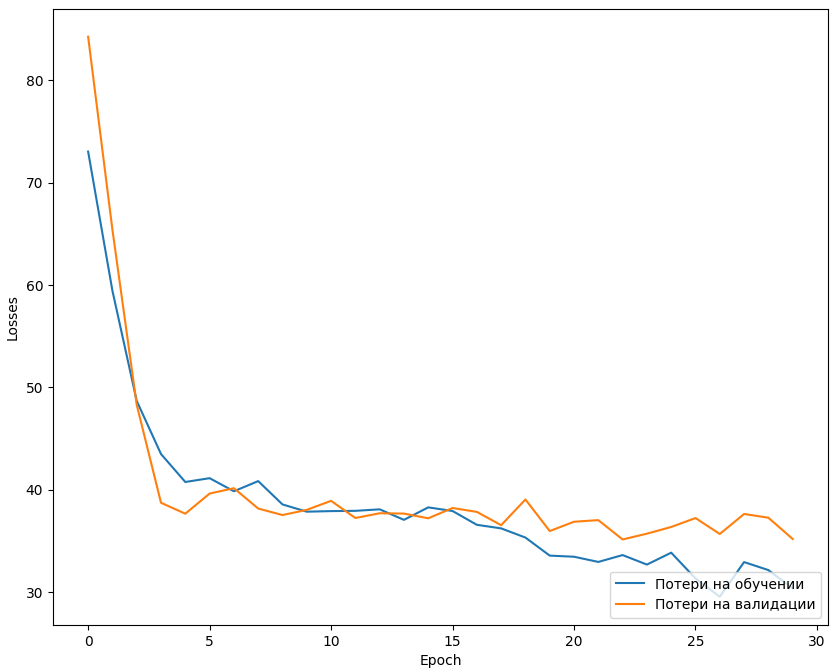
Рисунок 16 – График потерь на тренировочной и валидационной выборках
Вывод
В ходе выполнения лабораторной работы было обучено 2 нейронных сети.
Первая решает задачу регрессии на примере предсказания оценки ученика по математике по его характеристикам и особенностям окружения. Была выстроена последовательная полно связная сеть, использующая в качестве функции активации relu, а качестве функции потерь mse. Обученная сеть показала среднюю ошибку в 5 единиц от реальной оценки. Данное значение довольно существенно, можно предположить, что улучшению показателей способствует расширение набора данных. Проверено, что если включить в тренировочный набор оценки за первый и второй периоды, а целевым признаком назначить итоговую оценку, то средняя ошибка будет составлять уже 3 единицы, что гораздо лучше по показателям. Однако исходная задача состояла имено в предсказывании 1-ой оценки. Можно предположить, что имеющиеся характеристики не имеют высокого влияния на результат ученика.
Вторая нейросеть решает задачу бинарной классификации, определяя по характеристикам пациентов с сердечными заболеваниями принадлежность их к умершим или живым. Составлена последовательная полно связная НС с 2 слоями и функцией активации ReLu и Sigmoid. Полученная модель при обучении в 50 эпох имеет очень близкие значения потерь и метрики для тренировочной и валидационной выборок. Отклонение от истинного значения в среднем составляет 30%, так как задача бинарная - пациент либо принадлежит к классу, либо нет, то с полученными результатами модель можно считать относительно точной. Если сопоставить предсказанные результаты и истинные значения валидационной выборки, то окажется, что в 75% случаев НС правильно определяла класс пациента.
Предпринята попытка построить более эффективную модель для первой задачи. Изучены новые слои в Keras: Dropout. Достигнуто снижение разницы между тренировочными и валидационнмыи данными.
