Часть 2. Задача классификации.

Весь код первой части приведен в Приложении B.

Произведена загрузка данных. Проверено отсутствие пропусков в наборе (Рисунок 9). Все значения количественные, но имеют разные диапазоны, поэтому выполнена стандартизация при помощи приведения всех чисел к значениям от 0 до 1.

Рисунок 9 – Загрузка и проверка данных

Далее отделены входные данные - все столюцы, кроме целевого признака - события смерти. Входные данные подразделены на тренировочную и валидационную выборки в соотношении 5 к 1.

Создана последовательная модель, состоящая из 2 плотных слоёв, использующих функцию активации ReLU, т.к. в первом слое много нейроном, и Sigmoid, так как она хорошо справляется с задачей бинарной классификации.

В первом слое 12 нейроном, и 12 входов, так как именно столько есть значимых полей. В выходном слое 1 нейрон, выходной результат которого должен показывать вероятность принадлежности к классу умерших или живущих пациентов.

В качестве функции потерь взята рекомендованная binary_crossentropy: бинарная перекрестная энтропия, также применяющаяся в бинарной классификации. Для минимизации функции потерь используется алгоритм 'adam'. В качестве метрики качества выбрана mae - средняя абсолютная ошибка.

Выполнено обучении НС в 50 эпох (Рисунок 10). В процессе обучения потери постепенно снижаются и к концу обучения составляют около 0.5. Валидационные потери имеют примерно то же значение, поэтому можно судить об отсутствии переобучения сети. Среднее отклонение между предсказанными и истинными значениями для валидационных данных составляет 0.37.То есть в среднем модель ошибается на 0.37 из 1, что не так уж и плохо.

Рисунок 10 – Обучение НС из второй части

На основе валидационных данных выполнено предсказание. Результат записан в массив y_h_pred. Далее сформирован датасет df_match_h из истинных и предсказанных значений.

Рисунок 11 – Датасет с истинными и предсказанными значениями

На основе полученных данных построен график ошибок на обучающей и валидационной выборке по эпохам обучения (Рисунок 12). Согласно графику потери на обучении постепенно снижаются, доходя до значения 0,475. Ведут себя аналогичном образом, значит параметры сети выбраны хорошо, а повысить точность можно расширением набора данных.

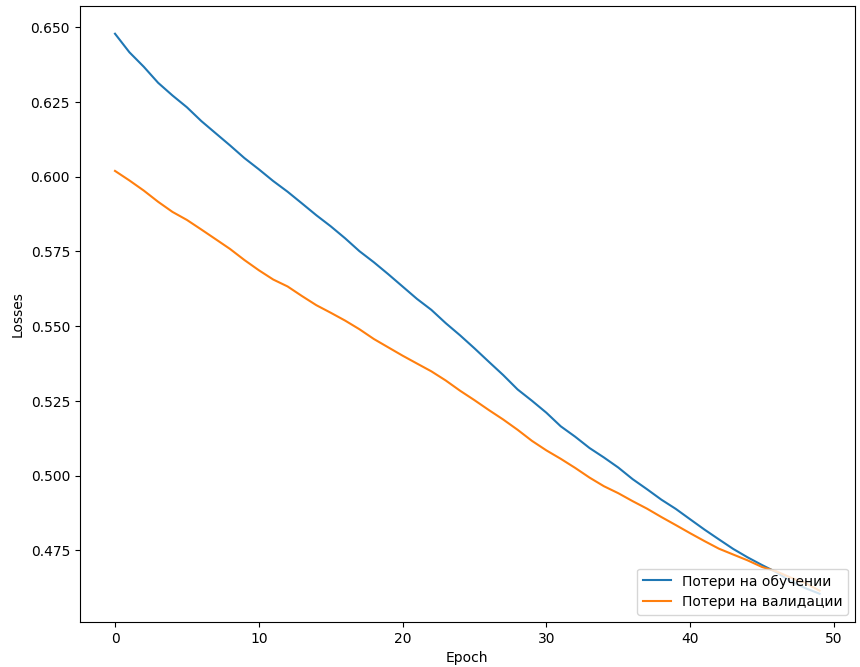
Рисунок 12 - Графики потерь на тренировочном и валидационном наборах

Также построен график, отображающий изменение метрики качества на обучающем и на валидационном наборе за каждую эпоху обучения (Рисунок 13).

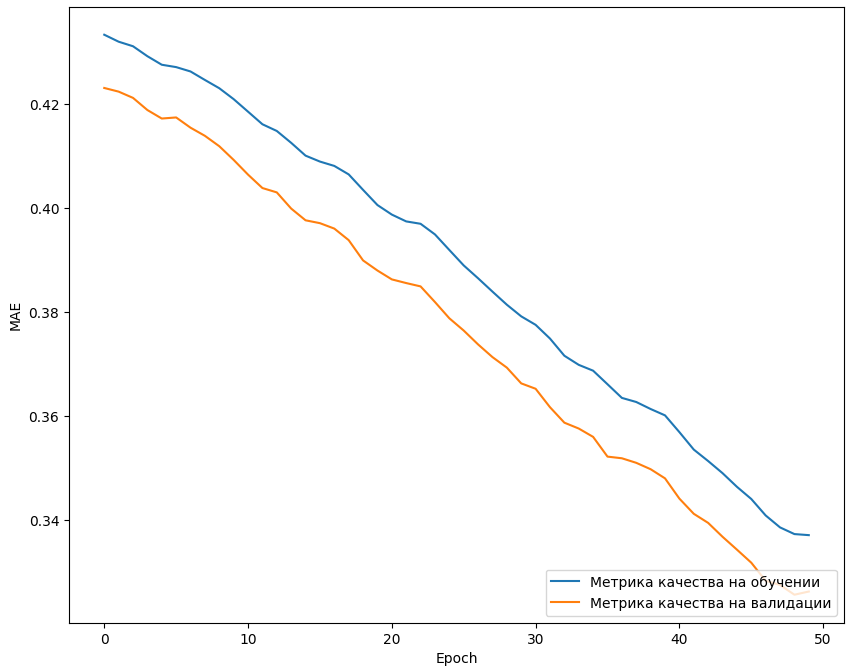
Рисунок 13 - Графики метрики на тренировочном и валидационном наборах

По графику видно, что среднее значение всех абсолютных ошибок прогнозирования, где ошибкой прогнозирования является разница между фактическим значением и прогнозным значением составляет 0,30 в конце обучения. На основе этого можно сделать вывод, что сеть выдает приближенно правильные результаты.

На завершающем этапе выстроена ROC-кривая (Рисунок 13). Она отображает зависимость количества верно классифицированных положительных примеров от количества неверно классифицированных отрицательных примеров.

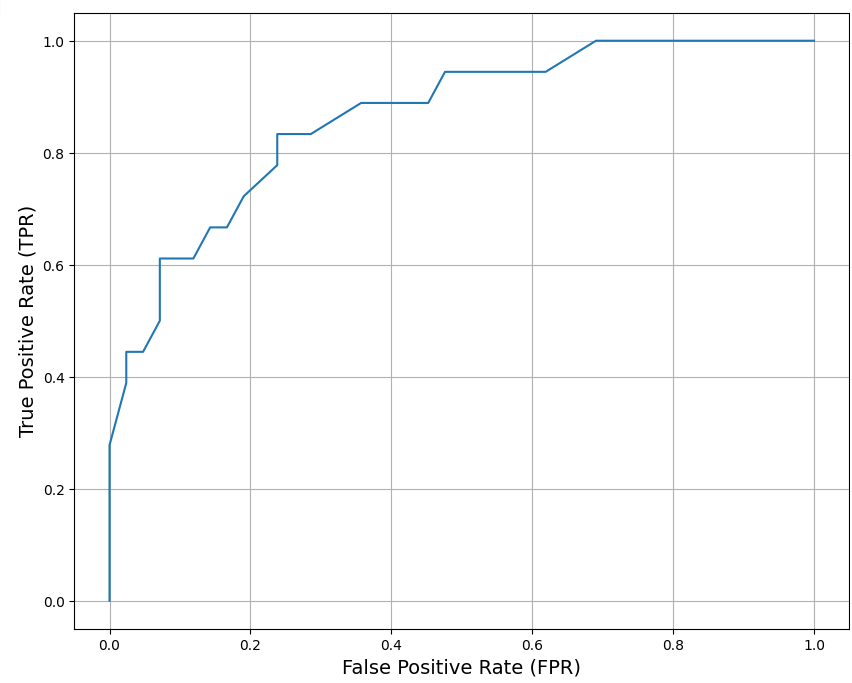
Рисунок 13 – Построенная ROC-кривая

По виду кривой можно сказать, что получившаяся модель лучше случайного предсказания, так как скачкообразно идет выше прямой y=x. Чем больше неверно-классифицированных отрицательных примеров тем больше верно классифицированных положительных примеров.

Оценка точности модели для валидационных данных приведена на Рисунке 14.

Рисунок 14 – Определение точности модели