Листинг 7 – Выполнение предсказаний

hopfield_net = HopfieldNetwork(size=SIZE)

patterns = [rectangle,triangle,circle]

hopfield_net.train(patterns)

failed_to_restore = []  # то что не восстановлено

def test_on_figure(figure,name,origin):

  predictions = []

  mistakes = []

  print(len(figure))

  for fig in figure:

    print('Фигура {0}\tОшибка {1}'.format(name,fig[1]))

    mistakes.append(fig[1])

    restored_pattern = hopfield_net.predict(fig[0])

    predictions.append([fig[0],restored_pattern])

    if ((restored_pattern.flatten()) != (origin.flatten())).any():

      failed_to_restore.append([name, fig[0], restored_pattern,fig[1]])     # Добавляем к списку проваленных название фигуры, ориганльную матрицу, предсказанную и уровень шума

    print("Зашумленный образ")

    plt.matshow(fig[0])

    plt.show()

    print("Полученное предсказание")

    plt.matshow(restored_pattern)

    plt.show()

    print("Исходный образ")

    plt.matshow(origin)

    plt.show()

    print("-"*100)

  return predictions, mistakes

   

p_rect, m_rect = test_on_figure(noisy_rectangles,'Квадрат',rectangle)

p_circl, m_circl = test_on_figure(noisy_circles,'Круг',circle)

p_tri, m_tri = test_on_figure(noisy_triangles,'Треугольник',triangle)

По полученному списку выводятся фигуры, которые сеть не смогла восстановить. Указывается название фигуры, исходный образ, уровень шума и полученный результат (Листинг 8).

Как видно по результатам (Рисунок 3), сеть ошибается при очень большом уровне шума, например в 90 пикселей или 100, что составляет 45 и 51 процентов зашумления (Рисунок 3).

Листинг 8 – Визуализация неверно восстановленных изображений

for fail in failed_to_restore:

  print("Зашумленный {0}\t Ошибка {1}".format(fail[0], fail[3]))

  plt.matshow(fail[1])

  plt.show()

  print("Полученное предсказание")

  plt.matshow(fail[2])

  plt.show()

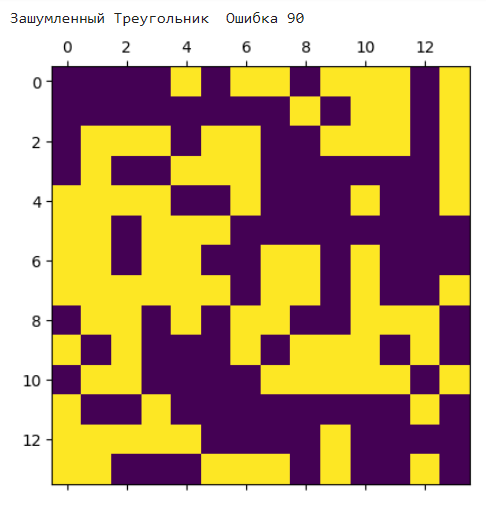
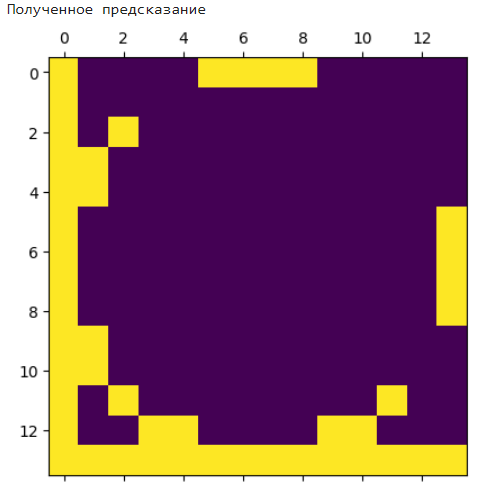
Рисунок 3 – Пример ошибочного распознавания образа

Произведено вычисление ошибки восстановления, равной отношению несовпадений предсказанного результата с эталонным и несовпадений тестовой матрицы с эталонной.

В функция calculate_error возвращает ошибку. Она выполняется для каждого выполненного предсказания при помощи цикла. В соответствующие фигурам массивы записываются результаты ошибок, после чего они визуализируются на графике, где по оси х расположен уровень шума, а по оси y - значение ошибки. Изменения ошибки в зависимости от эталонной фигуры выделяются разным цветом.

По полученным на графике линиям (Рисунок 4) видно, что в целом для разных фигур восстановление полностью выполняется при уровне шума не более 40 %. При уровне шума уже в 45 % ошибки для зашумленных квадратов резко возрастают, такая же тенденция наблюдается для зашумленных кругов и треугольников при шуме более чем в 50 %.

Листинг 9 – Вычисление ошибки восстановления

def calculate_error(origin, predicted, real):

    # Вычисление ошибки восстановления

    error = np.sum(real.flatten() != predicted.flatten()) / np.sum(origin.flatten() != predicted.flatten())

    if (np.sum(origin.flatten() != predicted.flatten())) != 0:

      error = np.sum(real.flatten() != predicted.flatten()) / np.sum(origin.flatten() != predicted.flatten())

    else:

      error = 0

    return error

# Сбор результатов для дальнейшего построения

def plot_errors(predictions,origin):

  errors = []

  for res in predictions:

    damage_error = calculate_error(res[0], res[1],origin)

    errors.append(damage_error)

  return errors

rect_errors = plot_errors(p_rect,rectangle)

circle_errors = plot_errors(p_circl,circle)

triangle_errors = plot_errors(p_tri,triangle)

plt.plot(m_rect,rect_errors,marker="o", color = 'b',label = "Квадрат")

plt.plot(m_circl,circle_errors,marker="o", color = 'r',label = "Круг")

plt.plot(m_tri,triangle_errors,marker="o", color = 'g',label = "Треугольник")

plt.legend()

plt.xlabel('Уровень шума %')

plt.ylabel('Ошибка')

plt.title('Зависимость ошибки восстановления от степени зашумления')

plt.grid(True)

plt.show()

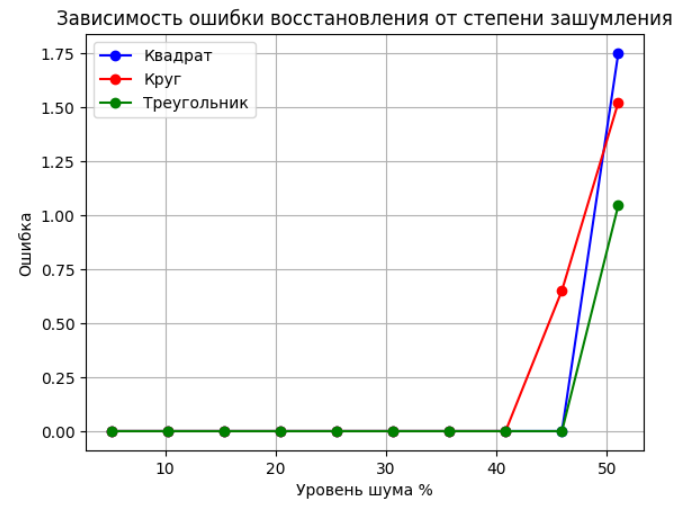
Рисунок 4 – График зависимости ошибки восстановления от уровня шума

Вывод:

В ходе выполнения лабораторной работы была построена нейросеть Хопфилда, состоящая из одного полно связного слоя нейронов и решающая задачу восстановления зашумленных изображений.

Сеть рассчитана на распознавание не более 28 образов, так как кол-во нейронов в сети составляет 196. Работа сети была проверена на восстановлении зашумленных изображения квадрата, круга и прямоугольного треугольника. Зашумленные и восстановленные данные были визуализированы, рассчитаны ошибки восстановления для каждого предсказания. На основе полученных данных построены графики зависимости ошибки восстановления от степени зашумления.

Выяснено, что нейросеть одинаково для всех фигур хорошо справляется с восстановлением образом, зашумленных менее чем на 80 %. При большем уровне зашумления ошибка восстановления резко растет, причем для квадрата гораздо быстрее, чем для треугольника и круга.

Дополнительное задание:

Добавление эталонного образа "Человек паук"

В начале создается матрица со значениями закрашенных клеток для генерации изображения маски Человека-паука. (Листинг 10). Изображение выведено на Рисунке 5.

Листинг 10 – Генерация нового эталонного образа “Человек-паук”

spider = np.ones((SIZE,SIZE),int) * (-1)

spider [3,3] = 1

spider[4,2] = 1

spider[4,4] = 1

spider[5,2] = 1

spider[6,2] = 1

spider[5,5] = 1

spider[6,5] = 1

spider[7,4] = 1

spider[7,3] = 1

spider [3,10] = 1

spider[4,9] = 1

spider[4,11] = 1

spider[5,8] = 1

spider[6,8] = 1

spider[5,11] = 1

spider[6,11] = 1

spider[7,10] = 1

spider[7,9] = 1

spider[10,3] = 1

spider [10,10] = 1

for i in range(4,10):

  spider[11,i] = 1

plt.matshow(spider)

plt.show()

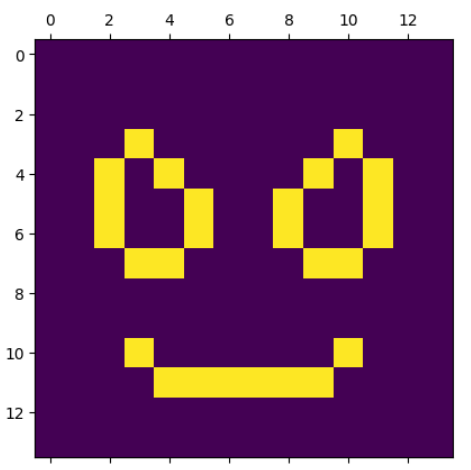
Рисунок 5 – “Человек-паук”

Сформированный эталонный образ включен в обучение. Создано зашумленное изображения с уровнем шума в 50 пикселей (примерно 25 % от всего изображения.) (Листинг 11)

Для зашумленного образа выполнено предсказание, сеть успешно восстановила образ, ошибка вычисления составила 0 (Рисунок 6).