ГУАП

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

доц., к.т.н., доц.				О.О. Жаринов
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №2

ОСНОВЫ ОБРАБОТКИ АУДИОСИГНАЛОВ СРЕДСТВАМИ PYTHON. МЕТОД ФИЛЬТРАЦИИ В СПЕКТРАЛЬНОМ ПРОСТРАНСТВЕ.

по курсу: МУЛЬТИМЕДИА-ТЕХНОЛОГИИ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. №	4117				А.В. Иванова
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2025

Цель работы:

Изучить основы обработки аудиосигналов на примере

метода фильтрации сигналов в спектральном пространстве.

Вариант 8:

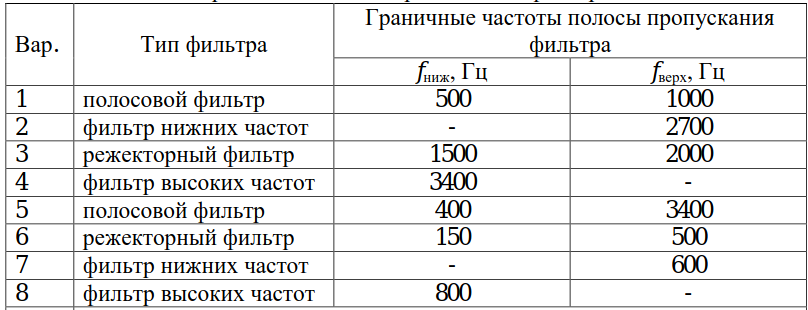
Рисунок 1 — Вариант задания

Краткие теоретические сведения:

Фильтрация является одним из широко применяемых методов обработки сигналов вообще и аудиосигналов в частности.

Идея метода фильтрации в спектральном пространстве (который также известен под названием “метод Фурье-фильтрации”) заключается в том, чтобы каким-то образом изменить спектр исходного сигнала и восстановить аудиосигнал из измененного спектра.

Таким образом, метод фильтрации реализуется в три шага:

1) производится вычисление спектра {Xn} исходного аудиосигнала {xn},

2) осуществляется изменение некоторого количества значений спектра

{Xn} в соответствии желаемыми частотными свойствами фильтра, в результате чего получается измененный спектр {Yn},

3) выполняется формировании выходного аудиосигнала посредством вычисления обратного преобразования Фурье спектра {Yn}.

Процедура изменения спектра исходного сигнала при реализации методов линейной фильтрации реализуется как поэлементное умножение двух массивов: исходного спектра {Xn} и предварительно сформированного массива значений передаточной функции фильтра {Wn}:

Y_n=W_n * X_n для n = 0, 1, N-1

При задании массива {Wn} исходят из требований к типу фильтрации. Например, если необходимо оставить без изменения частотные компоненты аудиосигнала в определенном диапазоне частот и максимально ослабить остальные компоненты, то используется следующий подход:

W_n = 1, для n соответствующим неизменяемым частотам;

W_n = 0, для n соответствующим подавляемым частотам

При реализации метода Фурье-фильтрации важно учитывать, что выходной сигнал, получаемый с помощью обратного преобразования Фурье (метод ifft в Python), должен быть вещественным, если соблюдено отношение мнимой части сигнала к реальной < 1e-6. Однако на практике, из-за ошибок округления при обработке больших массивов аудиоданных, в выходном сигнале может возникать заметная мнимая составляющая. Это затрудняет визуализацию и запись данных в файл. Поэтому на финальном этапе Фурье-фильтрации используется метод np.real(), который выделяет только вещественную часть массива. Однако его применение без должного контроля может скрыть ошибки манипуляции со значениями спектра, что может привести к нарушению указанного отношения.

Выполнение работы:

В качестве обрабатываемого звукового сигнала выбран фрагмент озвучивания почтальона Печкина с фразой «Извините, я почему вредный был — потому что у меня велосипеда не было» [2].

С помощью программы из первой работы получена спектрограмма звукового сигнала из файла (Рисунок 2). По ней видно, что наиболее слышим звук содержится в диапазоне частот от 100 до 1000 Гц, также есть выраженное звучание в частотах от 1000 до 1600 Гц.

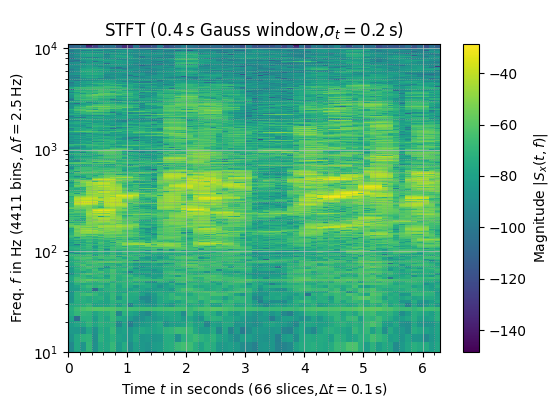
Рисунок 2 — Спектрограмма исходного сигнала

Посредством Python реализован метод Фурье-фильтрации высоких частот (Листинг 1). В начале посредство библиотеки librosa загруженный файл преобразован в массив описывающий звуковой сигнал, получены его характеристики: частота дискретизации 22050 Гц, 138816 отсчетов, 2 канала и 6 секунд длительности.

Вычислен амплитудный спектр сигнала через быстрое преобразование Фурье, реализованное методом fft из библиотеки numpy. Каждая точка спектра соответствует определённой частоте. В отдельную переменную записан спектр, переведенный в децибелы, для удобного восприятия на графиках.

Заданы границы частот для фильтра — в данном случае есть только нижняя граница 800 Гц. Получен массив n_dn — в котором записаны точки спектра с частотой равной нижней границе.

Задана функция фильтра W - массив где для точек с частотой выше 800 Гц значение 1, а для остальных нет. Исходный спектр умножается на W — таким образом остаются только точки с частотой от 800 Гц.

Полученный спектр также сохранен в отдельную переменную с преобразованием в децибелы для дальнейшего отображения. Из спектра с примененным фильтром через обратное преобразование Фурье получен новый аудиосигнал. Также применена функция np.real во избежание учета мнимой части. Также проверено, что отношение мнимой части к вещественной составляет менее 1e-6, а именно 3.5e-8.

Листинг 1 — Реализация фвс и обработка аудиосигнала

import numpy as np

import matplotlib.pyplot as plt

import librosa

import soundfile as sf

# Загрузка файла

file_name = 'potomu-chto-u-menya-velosipeda-ne-byilo.wav' # имя файла

input_signal, Fd = librosa.load('audio/' + file_name, sr=None, mono=False) # загрузка

# характеристики аудио

N = len(np.transpose(input_signal))

T = round(N / Fd)

t = np.linspace(0, T, N)

K = input_signal.ndim # количество каналов

print(K, N, Fd, T)

# спектр входного сигнала

Spectr_input = np.fft.fft(input_signal)

# преобразование в дБ:

AS_input = np.abs(Spectr_input)

eps = np.max(AS_input) * 1.0e-9

S_dB_input = 20 * np.log10(AS_input + eps)

# граничная нижняя частота в Гц

lower_frequency = 800

n_dn = round(N * lower_frequency / Fd) # индексы с частотами 800

# формирование преобразующей функции

W = np.zeros_like(Spectr_input) # массив из нулей

W[:,0:n_dn+1] = 1.0 # Оставляем низкие частоты

W[:,N-n_dn:N] = 1.0 # Оставляем низкие частоты в зеркальном спектре

W =1.0 - W # инверсия - оставляем наоборот высокие частоты

Spectr_output = Spectr_input * W # применение фильтра к спектру

# отношение мнимой части к реальной

print(np.max(np.abs(np.imag(np.fft.ifft(Spectr_output))))/ np.max(np.abs(np.real(np.fft.ifft(Spectr_output)))))

output_signal = np.real(np.fft.ifft(Spectr_output)) # получение нового сигнала

# получение спектра для спектрограммы и графиков

Spectr_output_real = np.fft.fft(output_signal)

# преобразование в дБ

S_dB_output_real =

20*np.log10(np.abs(Spectr_output_real+eps))

f = np.arange(0, Fd/2, Fd/N)

S_dB_output_real = S_dB_output_real[:, :len(f)]

S_dB_input = S_dB_input[:, :len(f)]

# запись нового файла

sf.write('audio/out_'+file_name, np.transpose(output_signal), Fd)

На Рисунке 3 представлен график амплитудного спектра входного и выходного сигналов. Код построения графика приведён в Листинге 2. На нем видно, что выходному сигналу соответствуют только отсчёты с частотой больше 800 Гц.