ГУАП

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

доц., к.т.н., доц.				О.О. Жаринов
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №3

Изучение методов фильтрации аудиосигналов в Python. Применение рекурсивных фильтров.

по курсу: МУЛЬТИМЕДА-ТЕХНОЛОГИИ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. №	4117				А.В. Иванова
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2025

Цель работы:

Получить навыки обработки аудиосигналов на примере методов фильтрации сигналов во временной области с использованием рекурсивных цифровых фильтров.

Вариант 8:

Рисунок 1 — Вариант задания

Краткие теоретические сведения:

Фильтрацию можно производить без вычисления спектра обрабатываемого оцифрованного аудиосигнала, непосредственно во временной области. Уравнение работы рекурсивного цифрового фильтра имеет вид:

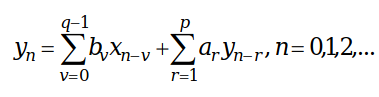
Формирование массива отсчётов выходного сигнала происходит последовательно. Данный способ фильтрации как для обработки записанных аудиосигналов, так и для потокового аудио, так как длина входного и выходного сигналов не ограничена.

Задача расчёта рекурсивного фильтра заключается в выборе так называемого аналогового фильтра-прототипа некоторого порядка, и вычислении коэффициентов {ar} и {bv}, при которых будет обеспечиваться желаемая частотная характеристика фильтра.

Для расчёта фильтров существуют разные методы, наиболее простым из которых является метод обобщённого билинейного преобразования передаточной функции аналогового фильтра-прототипа, который и реализован в соответствующих стандартных функциях и методах Python. Фильтры-прототипы бывают разных семейств (Баттерворта, Чебышева, и т. п.) и могут быть разных порядков. Чем выше порядок фильтра-прототипа, тем резче будет выражен переход от полосы пропускания к полосе подавления на частотной характеристике итогового РЦФ, но при этом увеличивается объем вычислений и возникает ряд дополнительных нюансов.

Выполнение работы:

В качестве обрабатываемого звукового сигнала выбран фрагмент озвучивания почтальона Печкина с фразой «Извините, я почему вредный был — потому что у меня велосипеда не было» [2].

С помощью программы из первой работы получена спектрограмма звукового сигнала из файла (Рисунок 2). По ней видно, что наиболее слышимый звук содержится в диапазоне частот от 100 до 1000 Гц, также есть выраженное звучание в частотах от 1000 до 1600 Гц.

Рисунок 2 — Спектрограмма исходного сигнала

На основе теоретических сведений посредством модуля signal Python библиотеки scipy реализован рекурсивный цифровой фильтр высоких частот семейства Баттерворта с частотным срезом в 800 Гц. В начале произведена загрузка звукового файла, обработка сигнала и получение его характеристик. Затем аудиосигнал преобразован согласно параметрам фильтрации через метод signal.butter. Полученный звуковой файл сохранен. Код программы приведен в Листинге 1.

Листинг 1 — Реализация рекурсивного цифрового ФВЧ

import numpy as np # для работы с данными

import matplotlib.pyplot as plt # для графиков

import librosa # для загрузки аудио

import soundfile as sf # для записи аудио

from scipy import signal # для ФВЧ

# Загрузка файла

file_name = 'potomu-chto-u-menya-velosipeda-ne-byilo.wav' # имя файла

input_signal, Fd = librosa.load('audio/' + file_name, sr=None, mono=False) # загрузка

# характеристики аудио

N = len(np.transpose(input_signal))

T = round(N / Fd)

t = np.linspace(0, T, N)

K = input_signal.ndim # количество каналов

print(K, N, Fd, T)

lower_f = 800

order = 20 # порядок фильтра-прототипа

sos = signal.butter(order, Wn =(lower_f / (Fd/2)), btype='highpass', output='sos')

output_signal = signal.sosfilt(sos, input_signal)

# Запись в файл нового сигнала

sf.write('audio/out_'+file_name, np.transpose(output_signal), Fd)

На Рисунке 3 представлен график амплитудного спектра входного и выходного сигналов. Код построения графика приведён в Листинге 2. На графике видно, что для выходного сигнала отсчёты с низкой частотой не слышны, пока значение частоты не будет приближено или выше 800 Гц. График выходного сигнала ведет себя также как и при использовании фильтрации Фурье, за исключением того, что в случае рекурсивного фильтра переход от полностью заглушённых частот плавный — звук постепенно нарастает начиная с частоты 700 Гц (Риуснок 4), а при использовании Фурье-фильтрации переход резкий.

Листинг 2 - Построение графика амплитудного спектра

# получение спектра сигналов для графика

Spectr_input = np.fft.fft(input_signal)

# преобразование в дБ:

AS_input = np.abs(Spectr_input)

eps = np.max(AS_input) * 1.0e-9

S_dB_input = 20 * np.log10(AS_input + eps)

Spectr_output_real = np.fft.fft(output_signal)

S_dB_output_real = 20 * np.log10(np.abs(Spectr_output_real+eps))

f = np.arange(0, Fd/2, Fd/N)

S_dB_output_real = S_dB_output_real[:, :len(f)]

S_dB_input = S_dB_input[:, :len(f)]

plt.figure(figsize=(6, 4))

plt.semilogx(f, S_dB_input[0, :], color='b', label=r'спектр входного сигнала')

plt.semilogx(f, S_dB_output_real[0, :], color='r', label=r'спектр выходного сигнала')

plt.grid(True)

plt.minorticks_on()

plt.grid(True, which='major', color = '#444', linewidth = 1)

plt.grid(True, which='minor', color='#aaa', ls=':')

Max_A = np.max((np.max(np.abs(Spectr_input)),

np.max(np.abs(Spectr_output_real))))

Max_dB = np.ceil(np.log10(Max_A))*20

plt.axis([10, Fd/2, Max_dB-120, Max_dB])

plt.xlabel('Частота (Гц)')

plt.ylabel('Уровень (дБ)')

plt.title('Амлитудный спектр входного и выходного сигналов')

plt.legend()

plt.show()

Рисунок 3 — Амплитудный спектр при фильтрации сигнала

Рисунок 4 — Фрагмент графика амплитудного спектра (650-850 Гц)

С помощью библиотеки matplotlib (Листинг 3) построены графики исходного и нового звуковых сигналов (Рисунок 4). Видно, что в случае с обработанным сигналом некоторые участки имеют амплитуду меньше, то есть звучат тише. Особенно это выражено на участках с 0 до 1 секунды, с 2.5 до 3.5 секунд, с 5.5 до 6 секунд. На записи на фоне разговора персонажа звучит музыка — скрипка и пианино. При фильтрации высоких частот звучание скрипки заметно заглушается. Голос Печкина, который теперь звучит выше, кажется более чётким и громким. В тоже время голос становится немного металлическим. На слух заметной разницы между выходными сигналами полученными через фильтр Фурье и рекурсивный фильтр нет. На графике можно заметить, что в случае рекурсивного фильтра переходы между заглушёнными частотами чуть более плавные.

# Выводим графики исходного аудиосигнала и после фильтрации:

start_t, stop_t = 0, T

plt.figure(figsize=(6, 3))

plt.subplot(2, 1, 1)

plt.plot(t, input_signal[0, :])

plt.xlim([start_t, stop_t])

plt.xlabel('Время (с)')

plt.ylabel('Амплитуда')

plt.title('Входной сигнал')

plt.subplot(2, 1, 2)

plt.plot(t, output_signal[0, :])

plt.xlim([start_t, stop_t])

plt.xlabel('Время (с)')

plt.ylabel('Амплитуда')

plt.title('Выходной сигнал')

plt.tight_layout()

plt.show()

Рисунок 5 — Сравнение входного и выходного сигналов

Для изучения влияния порядка фильтра на результаты фильтрации проведено несколько фильтраций исходного сигнала с разными порядками фильтра (4, 10 и 20). Построены соответствующие спектрограммы выходных сигналов (Рисунок 6-8). На спектрограммах видно, что чем выше порядок фильтра тем резче переход от подавляемых частот. Последняя спектрограмма с порядком 20 наиболее соответствует спектрограмме выходного сигнала полученной при Фурье фильтрации.

Если сравнивать спектрограмму выходного сигнала со спектрограммой входного, то чётко видно подавление частот меньших 800 Гц.

Рисунок 6 — Спектрограмма выходного сигнала, порядок 4

Рисунок 7 — Спектрограмма выходного сигнала, порядок 10

Рисунок 8 — Спектрограмма выходного сигнала, порядок 20

Выводы:

В результате выполнения лабораторной работы получены навыки обработки аудиосигналов на примере методов фильтрации сигналов во временной области с использованием рекурсивных цифровых фильтров.

В частности реализован и применён на практике рекурсивный фильтр высоких частот семейства Баттерворта. Была обработана запись озвучивания персонажа Печкина. В оригинале на записи слышен не очень высокий голос почтальона и звучание скрипки с пианино. После применения рекурсивного ФВЧ 20ого порядка голос Печкина становится выше, чётче, и звучит немного металлически. При этом заметно заглушается звучание скрипки.

Также на практике проверена зависимоть результатов фильтрации от порядка фильтра: чем выше порядок фильтра тем резче переход от подавляемых частот.

Обнаружена разница между рекурсивным фильтром и Фурье-фильтрацией: помимо более простой и быстрой работы рекурсивного фильтра, при его использовании переход от подавляемых частот к пропускаемым плавный (также зависит от порядка).

Список использованных источников

1. Жаринов О.О. Учебно-методические материалы к выполнению лабораторной работы №3 по дисциплине “Мультимедиа-технологии “. гр.4116,4117, 4118, Z0411. ГУАП, 2025. – 19 с. (Интернет-ресурс): //URL:

https://pro.guap.ru/inside/student/tasks/b1fa70870be81431ddf23edecfab3808/download

(Дата обращения 03.03.2025)

2. Zvukogram. База звуковых эффектов для монтажа. Категория Трое из Простоквашино //URL:

https://zvukogram.com/category/troe-iz-prostokvashino/

(Дата обращения 25.02.2025)