
Листинг 3 — Метод обработки изображения согласно параметрам
def img_filter(L, filter, d_high_k, title, is_binarization=False):
Spectr, Spectr_dB = get_spectr(L)
Min_S = np.min(np.abs(Spectr))
if Min_S != 0:
eps = Min_S
else:
eps = np.max(np.abs(Spectr)) * 1e-9
M, N = L.shape[0], L.shape[1] # размеры изображения
# размер области НЧ в спектре:
d_high = round(d_high_k * np.minimum(M, N))
mask_high = filter(M, N, d_high)
plot_spectr(Spectr_dB, 'Исходный спектр')
Spectr_high_pass_filtered = np.fft.fftshift(np.fft.fft2(L))
Spectr_high_pass_filtered *= mask_high # умножили на маску
# обратное двумерное БПФ:
high_pass_filtered = \
np.fft.ifft2(np.fft.ifftshift(Spectr_high_pass_filtered))
# контроль правильности работы
print(np.max(np.abs(np.imag(high_pass_filtered)))/ \
np.max(np.abs(np.real(high_pass_filtered))))
high_pass_filtered = np.abs(high_pass_filtered.real)
# нормировка
edges_high_pass = cv2.normalize(high_pass_filtered,None, 0.0, 1.0,cv2.NORM_MINMAX)
edges_high_pass = 1 - edges_high_pass # инвертировали
# бинаризация
if is_binarization:
edges_high_pass = binarization(edges_high_pass, 0.8)
# отображение результата
plot_img(edges_high_pass, ('ФНЧ: ', title, ' срез = ' , d_high_k))
# амплитудный спектр после применения маски:
Spectr_dB = 20*np.log10(np.abs(Spectr_high_pass_filtered)+eps)
Spectr_dB[0,0] = 20*np.log10(np.max(np.abs(Spectr)))
# вывод нового спектра
plot_spectr(Spectr_dB, 'Амплитудный спектр после ФВЧ (дБ)')
# нормировка яркости
cv2.imwrite('edges_high_pass.jpg',
cv2.normalize((edges_high_pass*255).astype('uint8'),None, 0, 255, cv2.NORM_MINMAX))
img_filter(L, simple_fft, 0.2, "Простая фильтрация") # простейшая Фурье Фильтрация
img_filter(L, simple_fft, 0.5, "Простая фильтрация") # простейшая Фурье Фильтрация
img_filter(L, simple_fft, 0.7, "Простая фильтрация") # простейшая Фурье Фильтрация
img_filter(L, butter_fft, 0.2, "Фильтр Баттерворта") # Фурье Фильтрация Баттерворта
img_filter(L, butter_fft, 0.5, "Фильтр Баттерворта") # Фурье Фильтрация Баттерворта
img_filter(L, butter_fft, 0.9, "Фильтр Баттерворта",True) # Фурье Фильтрация Баттерворта
canny(input_image) # оператор Кэнни
В начале исходное изображение обработано методом простейшей Фурье фильтрации с параметрами среза Dup равными 0.2 и 0.5. Полученные результаты приведены на Рисунках 3-4. Также на Рисунках 5-6 отображены спектры полученных изображений.
На основе полученных изображений можно сделать вывод о том, что чем больше берётся размер подавляемой области (размеры маски в данном случае зависят от величины d_high) тем больше низких частот удаляется и тем более выраженным получается эффект фильтра низких частот. Однако если брать слишком большую область обнуления, то слишком много низких частот удаляется и из-за этого теряются контуры (как на Рисунке 6)

Рисунок 3 — Простейшая фильтрация, d_high 0.2

Рисунок 4 — Простейшая фильтрация, d_high 0.5
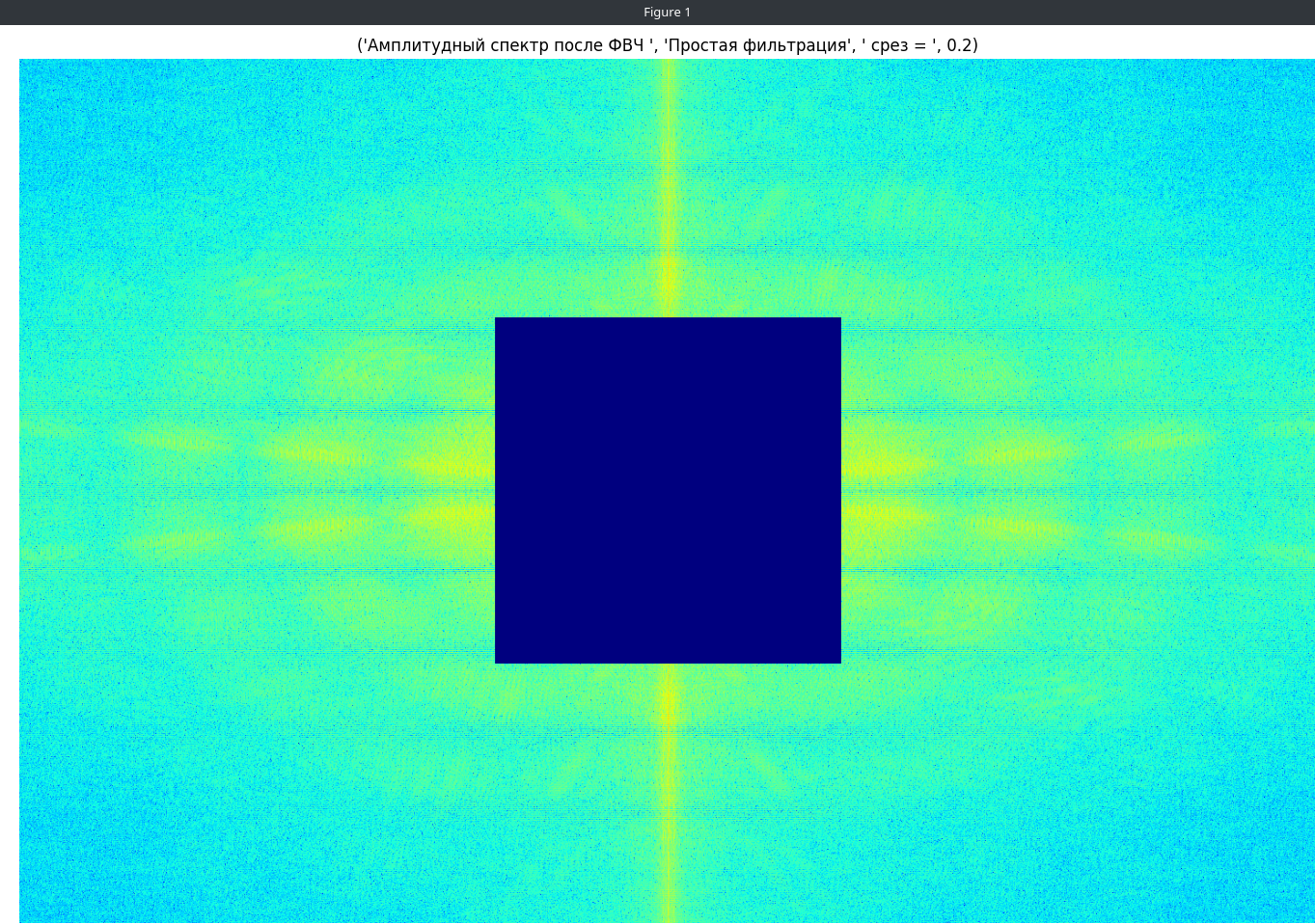
Рисунок 5 — Спектр полученного изображения (простейшая фильтрация , d_high 0.2)

Рисунок 6 - Спектр полученного изображения (простейшая фильтрация, d_high 0.5)
Далее исходное изображение было обработано при использовании более продвинутой Фурье фильтрации на основе фильтра Баттерворта. Были использованы параметры пространственной частоты среза 0.02 , 0.5 и 1. Полученные в результате изображения показаны на Рисунках 7-9. В соответствии с Рисунками 10-12 выведены отображения спектров полученных результатов.
В
фильтре Баттерворта (butter_fft)
малое значение среза
делает фильтрацию слишком сильной,
усиливая шум, а большое — даёт напротив
слишком плавный эффект. Слишком низкое
d_high
приводит к потере деталей, слишком
высокое — к размытию контуров.

Рисунок 7 — Фильтрация методом Баттерворта, срез 0.02

Рисунок 8 — Фильтрация методом Баттерворта, срез 0.5

Рисунок 9 — Фильтрация методом Баттерворта, срез 1
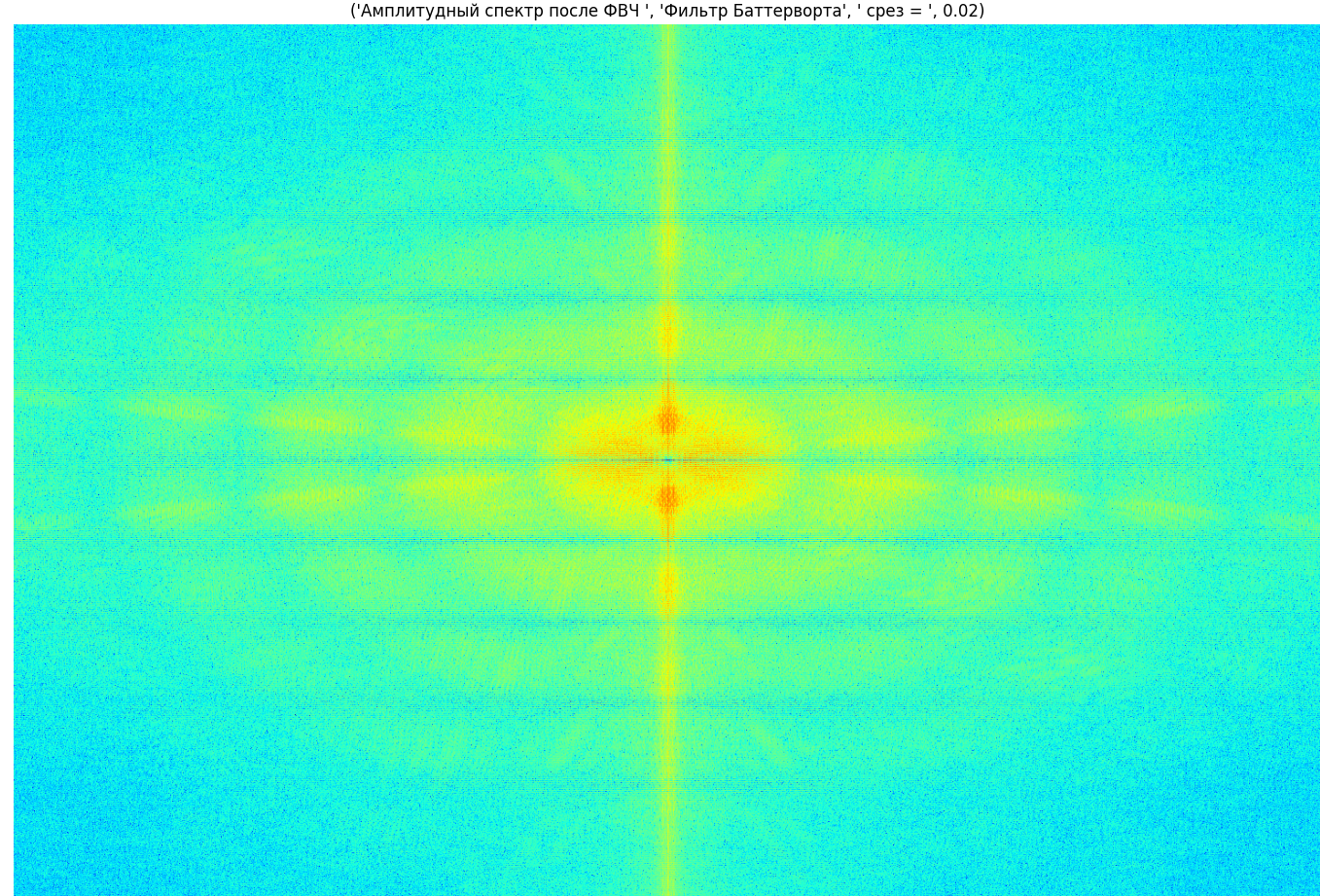
Рисунок 10 - Спектр полученного изображения (фильтрация Баттерворта, срез 0.02)
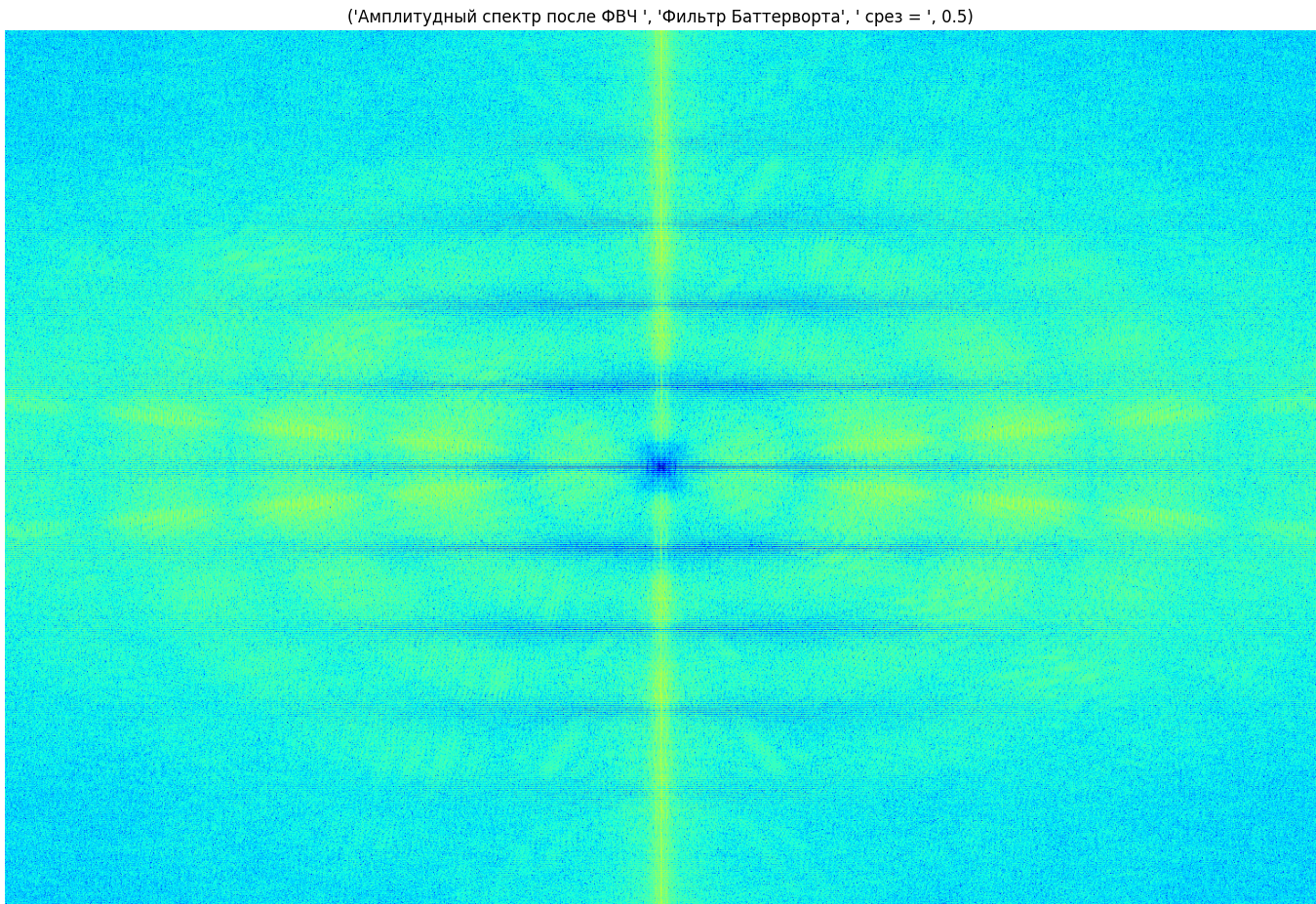
Рисунок 11 - Спектр полученного изображения (фильтрация Баттерворта, срез 0.5)
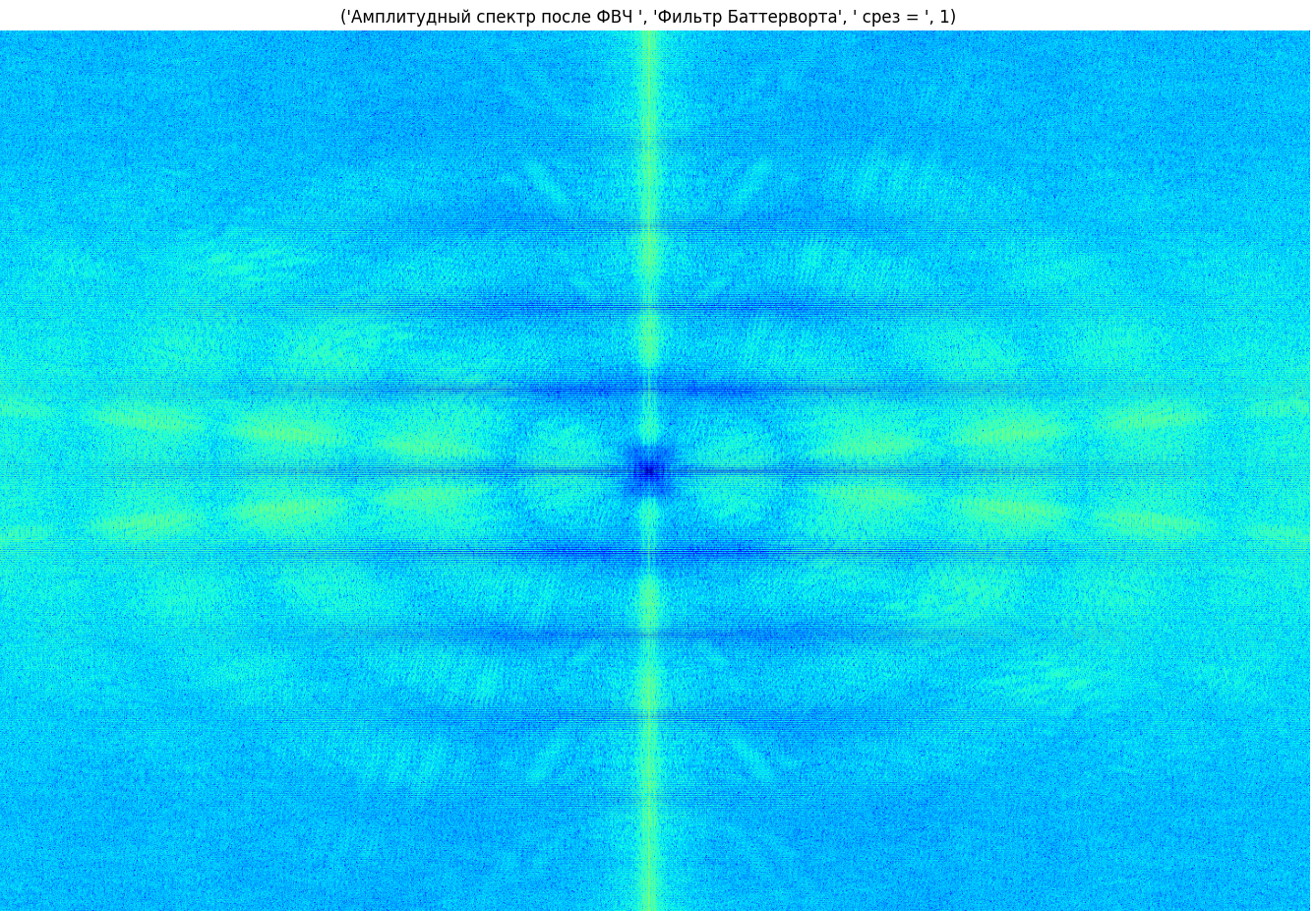
Рисунок 12 - Спектр полученного изображения (фильтрация Баттерворта, срез 1)
Далее исходное изображение была обработано посредством фильтрации Фурье-фильтром Баттерворта с оптимальным значением параметра частоты среза, равным 0.25, и последующей бинаризацией. Результат отображения продемонстрирован на Рисунке 13. Спектр полученного изображения выведен на Рисуке 14.
В результате получены достаточно чёткие контуры фигур, при этом не полученном изображении нельзя определить, какие фигуры изначально были чёрными, а какие белыми.
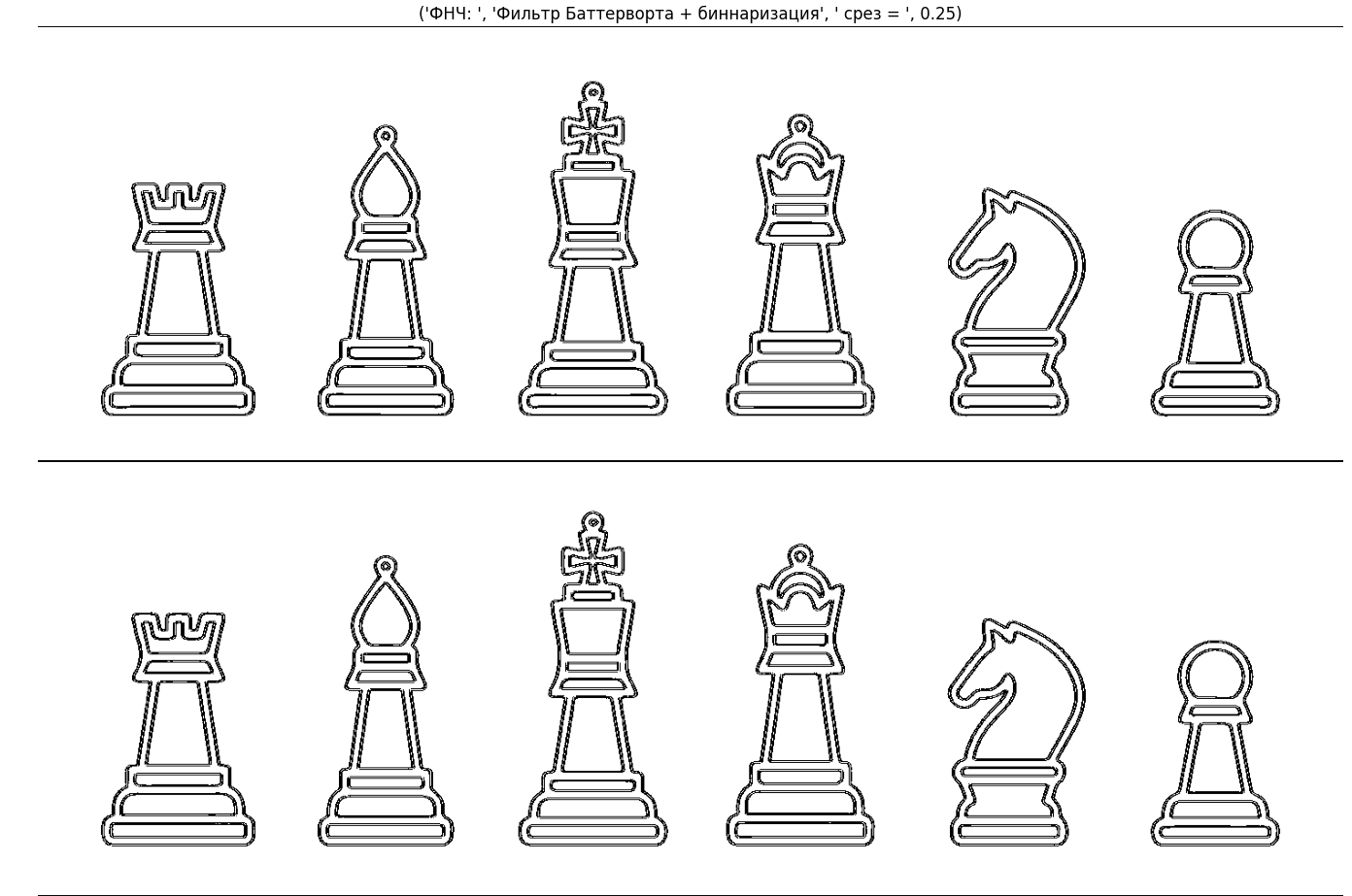
Рисунок 13 — Результат обработки изображения (Фильтр Баттерорта, срез 0.25, бинаризация)
Рисунок 14 — Спектр полученного изображения
Также опробован оператор Кэнни, позволяющий быстро реализовать фильтр низких частот изображения [2]. Результат, полученный при использовании данного модуля оказался наилучшим (Рисунок 15), так как контуры не только чёткие, но и отсутствуют лишние шумы, которые были получены при использовании фильтра Баттерворда.

Рисунок 15 — Результат оператора Кэнни
Полный программный код представлен в Приложении А.
