ГУАП

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

доц., к.т.н., доц.				О.О. Жаринов
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЁТ О ЛАБОРАТОРНОЙ РАБОТЕ №7

ОСНОВЫ ЦИФРОВОЙ ФИЛЬТРАЦИИ ИЗОБРАЖЕНИЙ. ПРОСТРАНСТВЕННЫЕ ФИЛЬТРЫ.

по курсу: МУЛЬТИМЕДИА-ТЕХНОЛОГИИ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. №	4117				А.В. Иванова
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2025

Цель работы:

Изучить основы обработки изображений на примере

методов фильтрации с использованием пространственных фильтров.

Вариант 8:

Р исунок 1 — Вариант искожения

Краткие теоретические сведения:

Фильтрация является одним из широко применяемых методов обработки изображений. Математически принцип линейной пространственной фильтрации изображения, представленного матрицей {I[m,n]}, описывается следующей формулой:

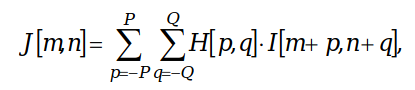
где массив коэффициентов H называется маской или ядром (kernel) фильтра и полностью определяет его свойства.

Пространственная фильтрация предполагает выполнение операции взвешенного суммирования значений пикселей исходного изображения в некоторой окрестности для каждого пикселя для всех индексов n и m.

Чёткость изображения является одним из критериев его качества. Основная идея повышения чёткости изображения заключается в добавлении к исходному размытому изображению дополнительного изображения, в котором подчёркнуты компоненты границ объектов, с некоторым весовым коэффициентом. Чаще всего в качестве дополнительного используют изображение, полученное из исходного изображения обработкой фильтром Лапласа.

Сложность коррекции фокусировки увеличивается при "смазывании" изображения, вызванном движением фотоаппарата. Методы компенсации таких искажений слишком сложны для описания в методических указаниях, но в Python есть несколько подходов. В данной лабораторной работе рассматриваются три метода: две разновидности инверсной винеровской фильтрации и метод Люси-Ричардсона.

Восстановление изображения из смазанного называется деконволюцией, основанной на предположении о свертке с искажающей маской, которая может быть известной, частично известной или неизвестной. Некоторые методы требуют задания маски, другие — нет (методы слепой деконволюции). Первые более эффективны при точном задании маски, но при неточностях эффективность снижается. Устойчивых алгоритмов для идентификации искажений не существует, поэтому исследователи используют рабочие гипотезы или подбирают параметры искажающей модели, основываясь на конечном результате.

Выполнение работы:

Часть 1:

В первой части необходимо подвергнуть исходное качественное модельное изображение искажению типа “смазывание”, и запустить на выполнение программу, которая обеспечит компенсацию внесённых искажений двумя методами восстановления изображений, передавая в них истинную маску искажений. Выбранное для работы изображение представлено на Рисунке 2.

Рисунок 2 — Исходное изображение

В Листинге 1 представлена программа реализации сферической расфокусировки и искажением исходного изображения. Взятый радиус круга — 5.

Листинг 1 — реализация сферической расфокусировки

import cv2

import numpy as np

# сферическая расфокусировка

def spherical_blur_mask(r):

grid_size = 2 * r + 1 # Диаметр маски

y_coords, x_coords = np.ogrid[-r:r + 1, -r:r + 1] # Координатная сетка для круга

# Круг x² + y² ≤ r²

is_inside_circle = (x_coords ** 2 + y_coords ** 2) <= (r ** 2)

# Заполнение маски: 1 внутри круга, 0 снаружи

mask = np.zeros((grid_size, grid_size), dtype=np.float32)

mask[is_inside_circle] = 1.0

mask = mask / np.sum(mask) # нормировка

return mask

# Загрузка картинки

path = 'img/p2'

input_image = cv2.imread(path+'.jpg')

# Радиус размытия

radius = 5

# Маска сферической расфокусировки

PSF_blur = spherical_blur_mask(radius)

print(PSF_blur)

# Применение размытия к изображению

blur_image = cv2.filter2D(input_image, -1, PSF_blur)

# Запись в файл результата

cv2.imwrite(path+'_blured.jpg', blur_image)

Результат искажения представлен на Рисунке 3.

Рисунок 3 — Полученное искажённое изображение (сферическая расфокусировка, радиус 5)

Далее выполнено восстановление искажённого изображения двумя способами. Первым задействован метод инверсной фильтрации Винера. Для реализации метода использована библиотека scikit-image. Написана функция wienner_deblur, принимающая в качестве параметров искажённое изображение, маску смазывания и коэффициент шума. Код функции представлен в Листинге 2. В качестве параметра шума было выбрано значение 0.01. Параметр был подобран вручную. При нем получается достаточно чёткая картинка в центре, а артефакты по краям на данном изображении не важны.

Листинг 2 — Реализация восстановления методом Винера

def wiener_deblur(blurred_image, psf, noise_var=0.01):

#Винеровская деконволюция

blurred_float = blurred_image.astype(np.float32) / 255.0

deblurred = np.zeros_like(blurred_float)

# Обработка каждого канала с явным noise_var

deblurred[..., 0] = restoration.wiener(blurred_float[..., 0], psf, noise_var)

deblurred[..., 1] = restoration.wiener(blurred_float[..., 1], psf, noise_var)

deblurred[..., 2] = restoration.wiener(blurred_float[..., 2], psf, noise_var)

return np.clip(deblurred * 255, 0, 255).astype(np.uint8)

# Винеровская деконволюция

restored = wiener_deblur(blur_image, psf, noise_var=0.01)

# Сохранение результата

cv2.imwrite(path+'_w_restored.jpg', restored)

Рисунок 4 — Восстановленное изображение (метод Винера)

В качестве следующего шага была использована функция restoration.richardson_lucy() для восстановления изображения, применяя метод Люси-Ричардсона. Этот метод, который является итеративным, часто применяется для восстановления изображений, размытых с помощью известной искажающей функции, в данном случае — маски PSF. Основная цель метода заключается в минимизации различий между размытым изображением и моделью, что способствует восстановлению утраченных деталей. Код реализации приведён в Листинге 3.

Для определения наилучшего количества итераций был реализован цикл, перебирающий значения от 1 до 20. Наиболее удовлетворительный результат был получен при 16 итерациях. Результат обработки выведен на Рисунке 5, можно отметить что центральное изображение не такое четкое, как в случае использования метода Винера, но и артефактов таких сильных нет.

Листинг 3 — Реализация восстановления методом Люси- Ричардсона

def richardson_lucy_deblur(blurred_image, psf, num_iter=10):

# Деконволюция методом Ричардсона-Люси

blurred_float = blurred_image.astype(np.float32) / 255.0

deblurred = np.zeros_like(blurred_float)

deblurred[..., 0] = restoration.richardson_lucy(blurred_float[..., 0], psf, num_iter=num_iter)

deblurred[..., 1] = restoration.richardson_lucy(blurred_float[..., 1], psf, num_iter=num_iter)

deblurred[..., 2] = restoration.richardson_lucy(blurred_float[..., 2], psf, num_iter=num_iter)

return np.clip(deblurred * 255, 0, 255).astype(np.uint8)

# Деконволюция Ричардсона-Люси (с подбором итераций)

for i in range(1,20):

rl_restored = richardson_lucy_deblur(blur_image, psf, num_iter=i)

# Сохранение результата

cv2.imwrite(f'{path}_rl_restored_iter{i}.jpg', rl_restored)

Рисунок 5 — Восстановленное изображение (метод Ричардсона-Люси)