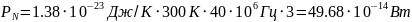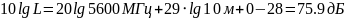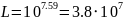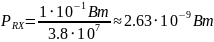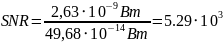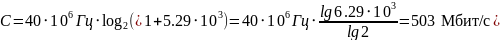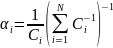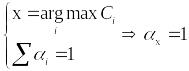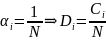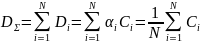МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное автономное образовательное учреждение высшего образования
«Санкт–Петербургский государственный университет аэрокосмического приборостроения»
ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ
ПРЕПОДАВАТЕЛЬ
Ассистент |
|
|
|
Н.В. Апанасенко |
должность, уч. степень, звание |
|
подпись, дата |
|
инициалы, фамилия |
ОТЧЁТ О ЛАБОРАТОРНОЙ РАБОТЕ №1 |
||||
МОДЕЛИРОВАНИЕ РАСПРЕДЕЛЕНИЯ РЕСУРСОВ НИСХОДЯЩЕГО КАДРА В ТЕЛЕКОММУНИКАЦИОННЫХ СЕТЯХ |
||||
по курсу: МОДЕЛИРОВАНИЕ СИСТЕМ РАСПРЕДЕЛЕНИЯ РЕСУРСОВ |
||||
|
||||
|
||||
РАБОТУ ВЫПОЛНИЛ
СТУДЕНТ ГР. № |
4117 |
|
|
|
Иванова А.В. |
|
|
|
подпись, дата |
|
инициалы, фамилия |
Санкт-Петербург 2025
Цель лабораторной работы
Получение навыков моделирования стандартных сценариев работы телекоммуникационных систем с топологией типа «звезда». Изучение свойств алгоритмов планирования ресурсов нисходящего кадра в подобных системах, на примере алгоритмов Equal Blind, Proportion fair, Maximum Throughput.
Вариант 8
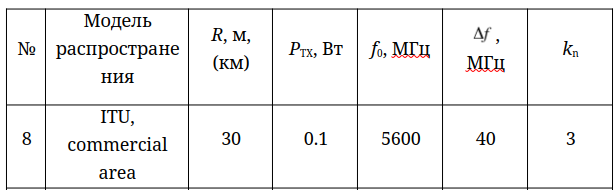
Рисунок 1 — Вариант задания
Пример расчёта параметров моделируемой системы
Расчёт
мощности шума:
|
(1) |
2) Расчёт уровня потерь в канале связи (для конкретного АБ) для модели ITU Commercial area:
|
(2) |
Перевод из «дБ» в «разы»:
|
(3) |
3) Расчет мощности сигнала, принятой АБ:
|
(4) |
4) Расчет отношение сигнал/шум:
|
(5) |
5) Расчет пропускную способность канала связи:
|
(6) |
Анализируемые алгоритмы распределения ресурсов:
Алгоритм Equal Blind
Данный алгоритм обеспечивает равные скорости между всеми абонентами. Доля ресурса времени, выделяемая каждому абоненту:
|
(7) |
Скорость для абонента i может быть выражена как:
|
(8) |
Алгоритм Maximum Throughput:
Данный алгоритм максимизирует суммарную скорость передачи Доля ресурса времени, выделяемая каждому абоненту, находится как:
|
(9) |
Алгоритм Proportion Fair:
Данный алгоритм выделяет равные доли ресурсов всем абонентам. Доля ресурса времени, выделяемая каждому абоненту, находится как:
|
(10) |
Суммарная скорость:
|
(11) |
1.1 Пример сгенерированных расположений абонентов
На Рисунке 1 представлен пример расположения 5000 абонентов. Такое количество абонентов выбрано, чтобы также провести тест распределения на плоскости.
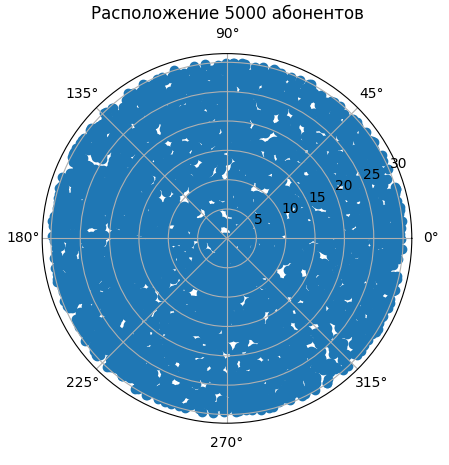
Рисунок 1 – Пример распределения 5000 абонентов.
Из графика расположения абонентов на Рисунке 1 видно, что практически вся допустимая область распределения абонентов заполнена, соответственно абоненты расположены равномерно.
Для подкрепления утверждения о равномерности распределения абонентов построена гистограмма распределения углов абонентов, представленная на Рисунке 2.
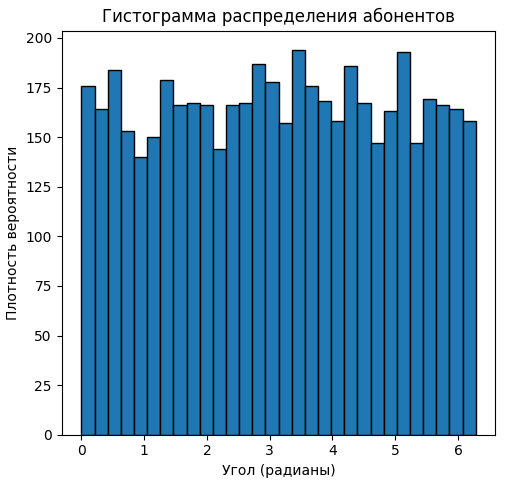
Рисунок 2 — Гистограмма распределения положения абонентов
Из графика, представленного на Рисунке 2, видно, что для каждого возможного значения выбора угла для расположения абонента в окружности примерно одинаковая вероятность. То есть примерно с равной вероятностью абонент может быть расположен в любой точке окружности.
Также, в соответствии с Рисунком 3 построен график эмпирической функции распределения абонентов.
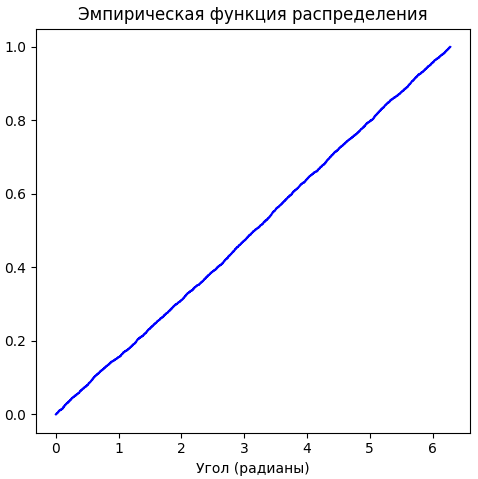
Рисунок 3 — Эмпирическая функция распределения положения абонентов
На графике, представленном на Рисунке 3, видно, что эмпирическая функция распределения возрастает, что подтверждает равномерное распределение абонентов.
Результаты моделирования
На рисунке 2 представлен график зависимости средней суммарной скорости передачи данных от количества абонентов для каждого алгоритма распределения ресурсов.
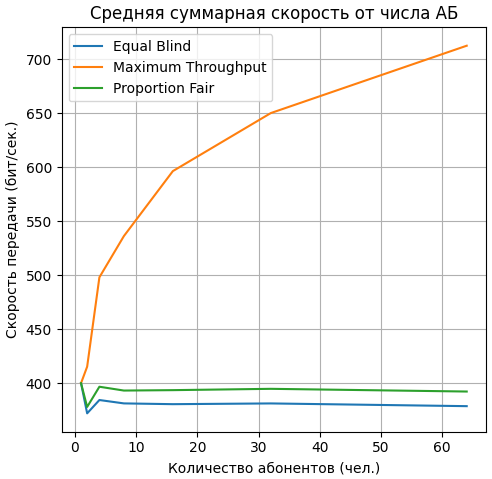
Рисунок 2 – График зависимости средней суммарной скорости передачи данных от количества абонентов
Из графика, представленного на рисунке 2, видно, что при увеличении количества абонентов средняя суммарная скорость передачи данных быстро растёт при использовании алгоритма Maximum Throughput, так как с ростом числа пользователей увеличивается и сумма их различных скоростей.
В случае использования алгоритма Proportion Fair видно, что устанавливается довольная стабильная равная скорость для всех абонентов, постепенно убывающая по мере их добавления.
Чуть более медленная суммарная скорость получается при использовании алгоритма Equal Blind, так как всем абонентам задаётся одинаковая скорость, при росте их количества скорость передачи снижается.
На рисунке 3 представлен график зависимости средней скорости передачи данных от количества абонентов.
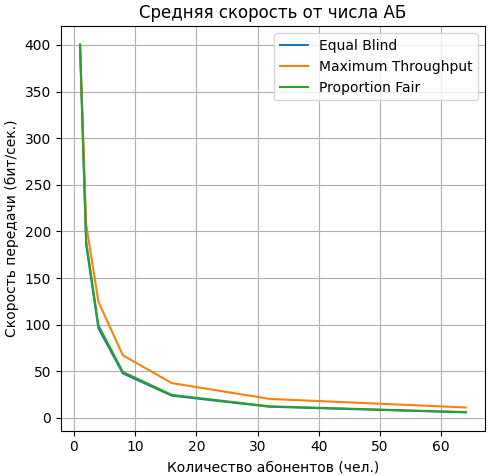
Рисунок 3 – График зависимости средней скорости передачи данных от количества абонентов
Из графика, приведённого на рисунке 3, видно, что зависимость скорости передачи данных от количества абонентов в сети схожа при использовании всех трёх алгоритмов: по мере увеличения количества абонентов увеличивается и число абонентов с низкой пропускной способностью, а следовательно средняя скорость передачи для всех абонентов падает.
Если результаты для алгоритмов Equal Blind и Proportion Fair практически одинаковы, то алгоритм Maximum Throughput показал результат немного лучше, так как в этом случае для абонентов, близко расположенных к станции, будет высокая скорость передачи данных.
На рисунке 4 представлен график зависимости средней минимальной скорости передачи данных от количества абонентов.
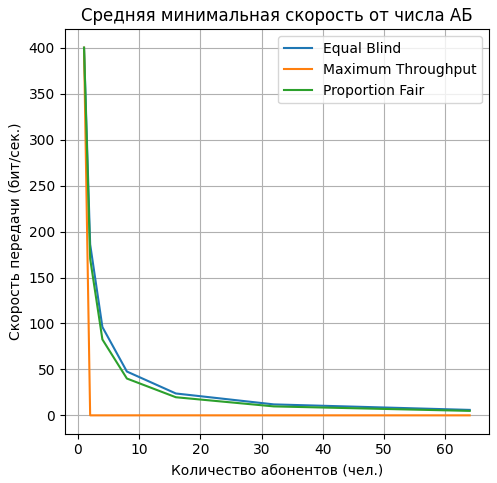
Рисунок 4 – График зависимости средней минимальной скорости передачи данных от количества абонентов
Из графика, представленного на рисунке 4, видно, что результаты для алгоритмов Equal Blind и Proportion Fair вновь схожи: при увеличении числа абонентов средняя минимальная скорость передачи данных снижается, так как происходит распределение нагрузки. В случае же алгоритма Maximum Throughput все ресурсы базовой станции распределяются на первого абонента, так как алгоритм отдаёт предпочтение абоненту с наивысшей пропускной способностью.