27. Виды гидравлических сопротивлений и формулы для них.

Потери напора на трение h_t возникают за счёт работы сил трения на участках с равномерным движением (например, в прямых трубах постоянного по длине сечения)

Потери напора в местных сопротивлениях h_m возникают за счёт работы сил трения в местах изменения направления движения или живого сечения потока, а также одновременно и того и другого.

Местными сопротивлениями являются, например, все виды арматуры трубопроводов (например, соединительные колена и муфты, вентили и задвижки, расходометры и т.д.)

h_1-2 = hτ_(1-2) + hм_(1-2)

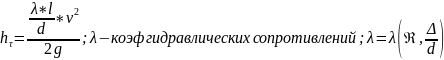
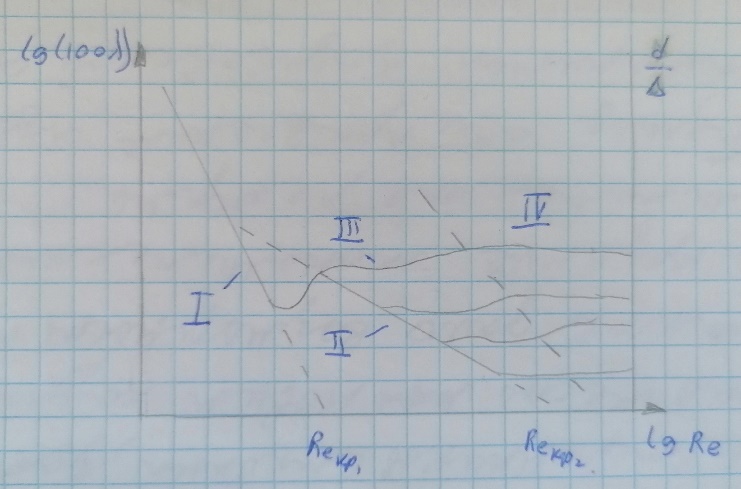
Рисунок 2 График Никурадзе

При ламинарном режиме: λ=64/Re ; Re < Reкр

При турбулентном режиме:

1) Гидравлически гладкие трубы ( Reкр < Re < 10* d/Δ )

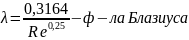
2) Зона смешенного трения (10* d/Δ < Re < 500 d/Δ )

3) Квадратичная зона (зона вполне шероховатых труб) (500 d/Δ < Re )

28. Режимы течений. Критические числа Рейнольдса.

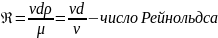
где μ, ν – динамический и кинематический коэффициенты вязкости.

Критерий Re позволяет судить о режиме движения жидкости в трубе. При значениях 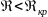– ламинарное течение жидкости, при 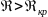– турбулентное, где – значение числа при . Более тщательные исследования показали, что в пределах изменения числа от 2000 до 4000 происходит периодическая смена режимов (так называемая перемежающаяся турбулентность). Поэтому условиями ламинарного и турбулентного режимов течения в трубах следует считать следующие значения числа Re:

Обычно в трубопроводе можно добиться перехода от ламинарного режима движения жидкости к турбулентному за счет увеличения расхода (скорости) жидкости. Опыты показывают, что для промышленных условий усредненное значение числа Рейнольдса Re_KP равно 2320.

29. Расход жидкости при ламинарном течении. Формула Пуазейля. Пути снижения потерь.

Вывод формулы Пуазейля:

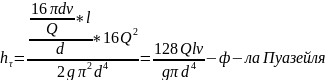
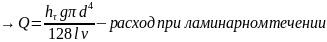
Формула Пуазейля справедлива только для ламинарных течений.

Пути снижения потерь

Потери напора по длине трубопровода определяются по формуле Дарси-Вейсбаха

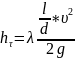
Где: l- длина участка трубопровода; d – диаметр; λ – безразмерный коэффициент гидравлического сопротивления; v – средняя скорость движения жидкости.

Чтобы понять, как потери зависят от различных параметров, подставим в формулу потерь

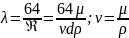
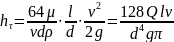
Следовательно, чтобы снизить потери, можно использовать жидкость с меньшей кинематической вязкостью, уменьшить длину трубопровода или расход жидкости. Или увеличить диаметр трубопровода.

30. Трубопроводы. Их классификация. Три основные задачи.

Трубопровод — инженерное сооружение, предназначенное для транспортировки газообразных и жидких веществ, пылевидных и разжиженных масс, а также твёрдого топлива и иных твёрдых веществ в виде раствора под воздействием разницы давлений в поперечных сечениях трубы.

Классификация трубопроводов

1. По схеме соединения труб:

Простые – трубопроводы постоянного сечения и не имеющие ответвлений

Сложные – делятся на последовательные (с различными сечениями), параллельные и разветвленные (имеющие общее сечение, в котором разделяются или смыкаются несколько ветвей труб)

2. По степени заполнения сечения труб жидкостью:

Напорные – трубопроводы, в которых поток жидкости не имеет свободной поверхности

Безнапорные – трубопроводы, в которых поток жидкости имеет свободную поверхность

Свободная поверхность жидкости – это поверхность раздела между жидкостью и газом (в частном случае может совпадать с поверхностью равного давления).

3. По соотношению потерь напора:

«Длинные» - трубопроводы, для которых потери напора на местных сопротивлениях малы по сравнению с потерями напора на трение по длине потока. В этом случае ими или пренебрегают за малостью, или учитывают через их ориентировочную суммарную эквивалентную длину, составляющую обычно несколько процентов от реальной длины «длинного» трубопровода. Примерами могут служить магистральные нефте- газо- проводы.

«Короткие» - трубопроводы, для которых потери напора на местных сопротивлениях соизмеримы с потерями напора на трение по длине потока. Для таких трубопроводов общие потери напора определяются с учётом коэффициентов местных сопротивлений или их эквивалентных длин.

Эквивалентная длина – такая длина прямого участка трубопровода данного диаметра, на которой потери на трение по длине эквивалентны потери напора, вызываемой данным местным сопротивлением

Примерами «коротких» трубопроводов могут служить всасываемые линии насосных установок, соединительные коммуникации с большим числом фасовых деталей и контрольно-измерительной аппаратуры и т.д.

ТРИ ОСНОВНЫЕ ЗАДАЧИ ГИДРАВЛИЧЕСКОГО РАСЧЕТА ПРОСТЫХ ТРУБОПРОВОДОВ

Условимся разность удельных потенциальных энергий на концах потока (или его участках) называть «действующим напором» Hд, т.е.

Тогда три основные задачи гидравлического расчёта простых трубопроводов можно сформулировать следующим образом:

1. Определение необходимого действующего напора по заданной производительности (расходу) трубопровода.

2. Определение пропускной способности трубопровода по заданному действующему напору.

3. Определение необходимого диаметра трубопровода для обеспечения заданной его производительности по заданному действующему напору.

Кроме того, для трубопроводов, работающих при давлении ниже атмосферного, возникает дополнительная задача выяснения возможности их нормальной эксплуатации.