21. Уравнение сохранения массы для линии тока.

(для струйки и для линии тока это одно и то же)

Для линии тока:

ω – осевая скорость

22. Уравнение сохранения массы для струйки и потока.

(для струйки и для линии тока это одно и то же)

Для струйки:

Для потока:

Поток состоит из бесконечного количества струек.

Проинтегрируем выражение (ур-е сохранения массы в диф форме для трубки тока) вдоль сечения

Предположим, что плотность может изменяться вдоль линии, а длина потока большая

– уравнение сохранения массы для потока

В каждом сечении это произведение будет постоянным, т.е.

23. Уравнение движения жидкости в напряжениях. Уравнение Бернулли для линии тока.

(23 и 24 в экзамене без уравнения движения жидкости в напряжениях)

Уравнение движения жидкости в напряжениях.

24. Уравнение движения жидкости в напряжениях. Уравнение Бернулли струйки и потока

Для струйки:

Для потока:

[z₁ + p₁/(ρg) + α₁υ₁²/(2g)] – [z₂ + p₂/(ρg) + α₂ υ ₂²/(2g)] = h_1-2.

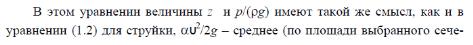
25. Уравнение Бернулли для реального потока. Физический смысл.

Вид уравнения:

Где Z – расстояние от произвольно-выбранной горизонтальной плоскости (плоскости сравнения) до центров тяжести соответствующих живых сечений;

P – абсолютное давление в центрах тяжести этих сечений;

V – средняя скорость движения жидкости в сечениях;

α – поправочный коэффициент на неравномерность распределения местных скоростей по живым сечениям потока.

Полным напором H называется суммарная удельная по весу энергия жидкости, проходящей через рассматриваемое живое сечение.

Составляющие полного напора представляют собой:

Z – Удельную потенциальную энергию положения («геометрическая высота положения» или «геометрический напор»)

– удельную потенциальную энергию давления («пьезометрическая высота» или «пьезометрический напор»)

– удельная кинетическая энергия («скоростная высота» или «скоростной напор»)

Потерями напора h_1-2 называется разность полных напоров на участке потока между сечениями 1 и 2, т.е. затраты энергии жидкости на работу сил трения при перемещении единицы её веса на рассматриваемом участке.

h_1-2 = H₁ – H₂

Нумерация сечений производится всегда по ходу течения жидкости.

Потери напора складываются из 2-х составляющих:

Потерь напора на трение по длине потока hτ и потерь напора в местных сопротивлениях hм, т.е. h_1-2 = hτ_(1-2) + hм_(1-2)

Физический смысл уравнения Бернулли. Уравнение Бернулли является следствием закона сохранения энергии. Сумма потенциальной (положения и давления) и кинетической энергии есть величина постоянная на всём пути движения потока жидкости.

26. Графическое представление уравнения Бернулли.

– гидравлический уклон

Где:

Полным напором H называется суммарная удельная по весу энергия жидкости, проходящей через рассматриваемое живое сечение.

Составляющие полного напора представляют собой:

Z – Удельную потенциальную энергию положения («геометрическая высота положения» или «геометрический напор»)

– удельную потенциальную энергию давления («пьезометрическая высота» или «пьезометрический напор»)

– удельная кинетическая энергия («скоростная высота» или «скоростной напор»)

h_о – общие потери на участке