
- •Предмет курса. Флюиды. Классификация. Границы, при которых материальное тело приобретает свойства флюида.
- •Гипотеза сплошной среды и гипотеза взаимопроникающих сред.
- •Плотность флюида. Многофазные и многокомпонентные флюиды.
- •Напряжение. Давление. Гидростатическое давление, свойства. Виды давлений.
- •Доказательство, что давление в любой точке флюида не зависит от наклона произвольной площадки, проведённой через эту точку.
- •Дифференциальные уравнения равновесия (уравнения Эйлера)
- •7. Уравнение поверхностей уровня (изобарических поверхностей) и их свойства.
- •8. Основное уравнение гидростатики несжимаемой жидкости.
- •9. Сила давления жидкости на плоские твердые поверхности. Точка приложения равнодействующей силы.
- •10. Сила давления жидкости на криволинейные поверхности. Нахождение вертикальной составляющей.
- •11. Сила давления жидкости на криволинейные поверхности. Нахождение горизонтальной составляющей.
- •12. Сила давления жидкости на тело, полностью погружённое в жидкость. Закон Архимеда.
- •13. Реологические уравнения. Теорема о сдвиговом течении.
- •14. Реологические кривые ньютоновских и неньютоновских флюидов.
- •15. Определение динамического напряжения сдвига. Физическое объяснение.
- •16. Гидростатика жидкостей, обладающих динамическим напряжением сдвига.
- •17. Равновесие и движение частиц во флюиде, обладающем динамическим напряжением сдвига. Силы, действующие на частицу, которая полностью погружена во флюид.
- •18. Максимальный диаметр частицы, не тонущей в впж.
- •19. Скорость жидкости, обеспечивающая витание частиц в ньютоновском потоке. Формула Риттингера.
- •20. Основные понятия гидродинамики.
- •21. Уравнение сохранения массы для линии тока.
- •22. Уравнение сохранения массы для струйки и потока.
- •23. Уравнение движения жидкости в напряжениях. Уравнение Бернулли для линии тока.
- •24. Уравнение движения жидкости в напряжениях. Уравнение Бернулли струйки и потока
- •25. Уравнение Бернулли для реального потока. Физический смысл.
- •26. Графическое представление уравнения Бернулли.
- •27. Виды гидравлических сопротивлений и формулы для них.
- •28. Режимы течений. Критические числа Рейнольдса.
- •29. Расход жидкости при ламинарном течении. Формула Пуазейля. Пути снижения потерь.
- •30. Трубопроводы. Их классификация. Три основные задачи.
- •Классификация трубопроводов
- •31. Бурящаяся скважина как сложный трубопровод. Формулы для определения забойного и устьевого давлений.
- •32. Местные сопротивления. Примеры местных сопротивлений. Внезапное расширение.
- •33. Переход к турбулентному течению впж. Формула Соловьева е.М.
- •34. Гидравлический удар. Формула Жуковского н.Е.
- •35. Основные понятия и определения подземной гидромеханики.
- •36. Опыт и закон Дарси.
- •37. Границы применимости закона Дарси.
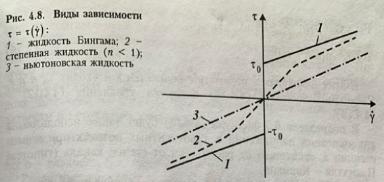
14. Реологические кривые ньютоновских и неньютоновских флюидов.
Пояснения бери из 13.
15. Определение динамического напряжения сдвига. Физическое объяснение.
Динамическое напряжение сдвига – напряжение, при приложении которого жидкость приобретает свойство текучести.
Физическое объяснение:
Заряженные частицы раствора, притягиваясь друг к другу разноимёнными зарядами, образуют внутреннюю структуру раствора, для разрушения которой требуется приложение дополнительной силы.
В статике прочность этой структуры возрастает со временем (СНС).
При течении раствора устанавливается динамическое равновесие между количеством вновь образуемых связей частиц и количеством разрушенных при сдвиге связей.
В соответствии с этим ДНС – мера прочности внутренней структуры раствора в динамических условиях.
Величина ДНС определяется силой электрохимического взаимодействия между частицами активной твёрдой фазы (глины, полимеров, дисперсантов).
ДНС зависит от:
Концентрации зарядов на поверхности / сколах частиц твёрдой фазы;
Объёмной концентрации твёрдой фазы;
Концентрации и типов ионов в жидкой фазе.
Если ввести в рассмотрение производную dw/dy, то она будет характеризовать скорость сдвига, т.е. разность скоростей слоёв жидкости, рассчитанную на единицу расстояния между ними. Оказывается, что для многих жидкостей справедлив закон, согласно которому касательное напряжение τyz между слоями пропорционально разности скоростей этих слоёв, рассчитанной на единицу расстояния между ними:

16. Гидростатика жидкостей, обладающих динамическим напряжением сдвига.
Рисунок 1. В трубке с поршнем налита вода. Если поршень внезапно убрать, то вода выльется.
Рисунок 2. В трубке с поршнем глинистый раствор. Если поршень внезапно убрать, то он не выливается, потому что не течет.
Рисунок 3. В трубке с поршнем глинистый раствор. Если к поршню приложить силу F, то, при определенном значении силы, раствор начнет двигаться.
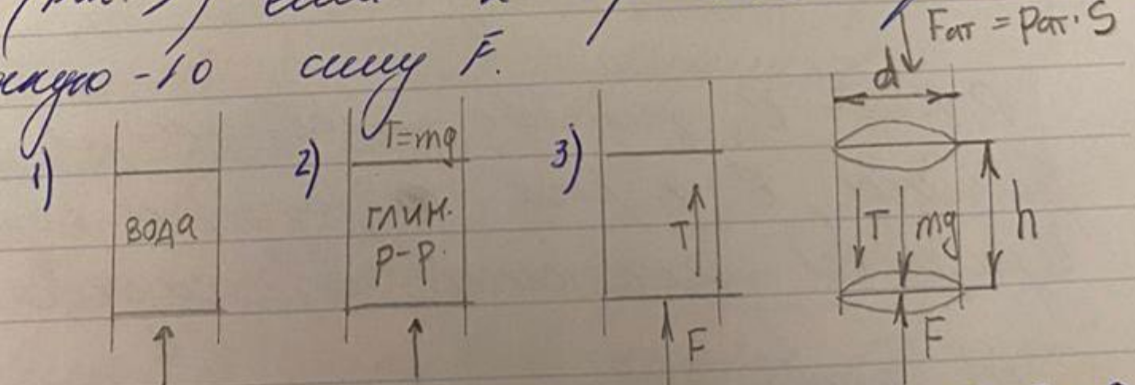

τ – касательные напряжение
T – касательная сила, действует на боковые поверхности цилиндра


Pвн – давление внизу; Pвв – давление вверху
Таким образом мы получили гидростатику флюида, учитывая напряжения в жидкости.
(1) Характеризует бесконечно много положений равновесия. Pвв мы не меняем, а Pвн ↑, растёт напряжение τ и достигает τ0. Напряжение τ зависит от наклона стенок.

Если мы приложим силу F сверху, то напряжение действует с другой стороны.


d – внутренний диаметр труб
(4) полностью характеризует все состояния равновесия (а их множество) для флюидов, образующих τ0
Как выбирать знаки?
Если F действует снизу, то «+», если сверху, то «-»
Уравнение (4) полностью характеризует все состояния равновесия.
h – длина ствола скважины. Если скважина
строго вертикальна, то h=H,
где H
– глубина скважины. Если скважина
наклонная, то h
= L
– длина ствола скважины. Если скважина
строго вертикальна, то h=H,
где H
– глубина скважины. Если скважина
наклонная, то h
= L
Для кольцевого пространства:

Где dг=dc-dн
 -
гидравлический диаметр; dс
– диаметр стенок скважины (долота); dн
– наружный диаметр БТ; dT
– внутренний диаметр трубы
-
гидравлический диаметр; dс
– диаметр стенок скважины (долота); dн
– наружный диаметр БТ; dT
– внутренний диаметр трубы
В 3-их слагаемых в уравнении (4) h следует заменить на L для наклонно-направленных скважин


